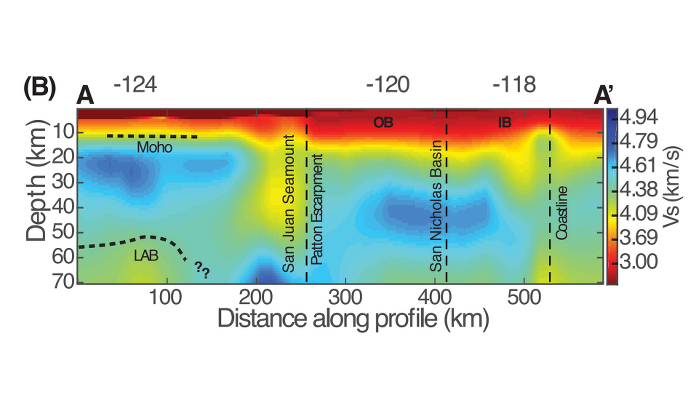
All blobs are equal, but some blobs are more interesting than other blobs. In this new Wit & Wisdom post, Jamie Ward, PhD student in seismology at the University of Leeds, United Kingdom, explores this age-old saying and discusses whether or not LLSVPs are the most important blobs in our lives. Also, there is a picture of a dog. It makes sense, I promise. Large Low Shear Velocity Provinces (LL ...[Read More]
Should we still study LLSVPs?
Tomography model S40RTS (Ritsema et al., 2011) at the CMB with velocity contours from -2 to 2 % δVs with increments of 0.5 % δVs.
Normally I’d add some kind of clever remark here, but it’s just a figure full of blobs. What can I say about that? Maybe that dogs are better? Scroll down for a dog! So proud that we finally have dog content on this blog.
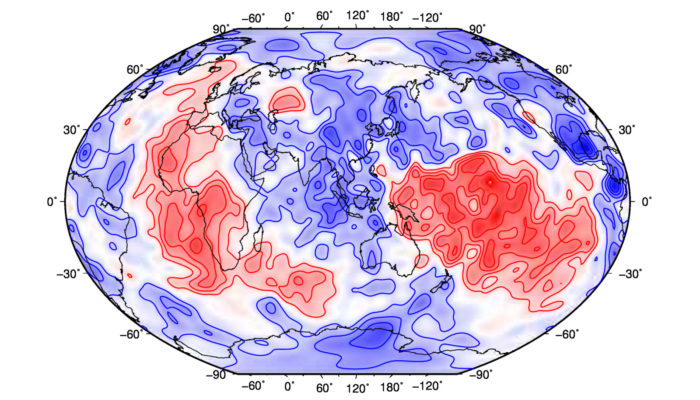
Normally I’d add some kind of clever remark here, but it’s just a figure full of blobs. What can I say about that? Maybe that dogs are better? Scroll down for a dog! So proud that we finally have dog content on this blog.
