GD
Geodynamics
Avatar photo

Iris van Zelst

Iris is a Patience Cowie research fellow at the University of Edinburgh. Her current research revolves around modelling the geodynamics and seismicity of Venus. Previous projects concerned subduction dynamics and the associated seismic and tsunami hazards. Iris is the former Editor-in-chief of the GD blog team and now sometimes just blogs for fun. You can reach Iris via email. For more details, please visit Iris' personal webpage or check out her youtube channel: youtube.com/irisvanzelst.

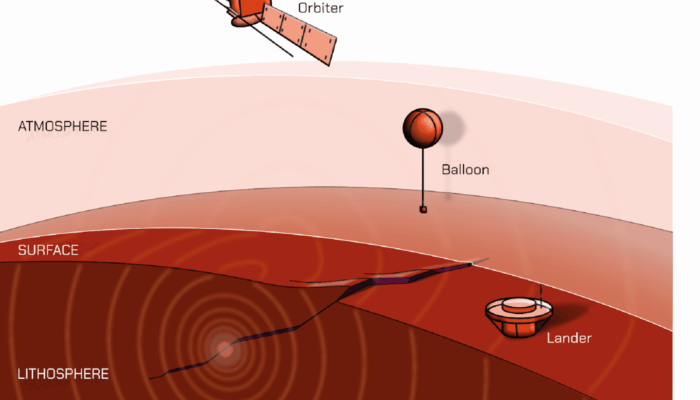
Iris van Zelst – GD Outstanding ECS Award 2025

and April 30, 2025
Iris van Zelst – GD Outstanding ECS Award 2025
Different methods to potentially detect seismic waves on Venus: a broadband seismometer on the surface, a pressure sensor on a balloon in the atmosphere, and an airglow imager on an orbiter around Venus (credit: Iris van Zelst / Fabio Crameri; also see Garcia et al., 2024).

The 2025 Outstanding Early Career Scientist Award of the Geodynamics Division was awarded to Iris van Zelst in recognition of her outstanding ability to connect research fields including earthquake dynamics, planetary sciences and geodynamics, along with her profound engagement with science outreach and promotion of diverse and inclusive working enviroments. In this interview, Iris -also former EG ...[Read More]

Notice! – Your public data has been collected to study the diversity of the geodynamics community over time

April 25, 2025

Dear Geodynamics community, This is your trusted former Editor-in-Chief speaking. I have an important announcement! In very exciting news, the team behind the 101 Geodynamic modelling paper (which I am sure you have read and loved, right? No? Well, what are you waiting for?! Check it out here!) has reunited to write another very relevant paper tailored to the geodynamics community. You’re we ...[Read More]

How we made QUARTETnary – the card game about the geological time scale

March 6, 2024
How we made QUARTETnary – the card game about the geological time scale
Ready to explore the history of the Earth and play QUARTETnary yourself? Back the Kickstarter now!

QUARTETnary is an educational card game about the geological time scale. Consisting of 60 beautifully illustrated cards, QUARTETnary explores the events in Earth’s history: from dinosaurs to humans and from the formation of the Alps to the formation of the Himalayas. It was designed by Iris van Zelst (me! Your fabulous former Editor-in-Chief), and illustrated by Lucia Perez-Diaz (also a former edi ...[Read More]

Science Sisters Season 2 is out now!

, and January 31, 2024
Science Sisters Season 2 is out now!
🎶 Science Sisters, they're here to talk 🎶

Science Sisters is a lighthearted interview series where Iris van Zelst (postdoc at the German Aerospace Center) chats with lots of different people (with a focus on – but not limited to – women in science) to make some sense of the academic world. Filled with laughter and silliness, it explores different career paths, academic life, soft skills, and current issues in academia. At 15 t ...[Read More]