GD
Geodynamics

numerical modelling

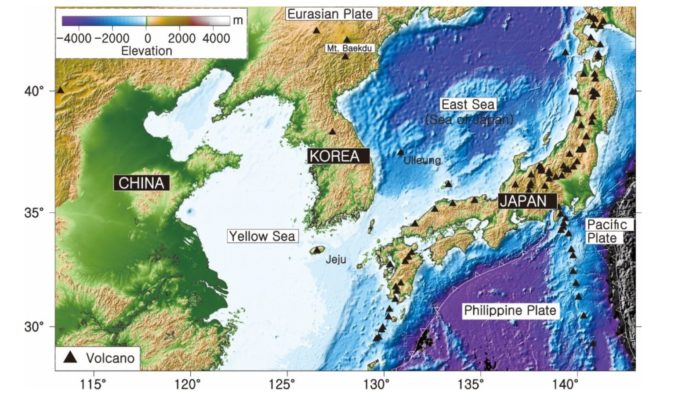
Arc and Intraplate Volcanism in Northeast Asia Since mid-Miocene: Numerical model studies

and January 11, 2023
Arc and Intraplate Volcanism in Northeast Asia Since mid-Miocene: Numerical model studies
Locations of the Quaternary arc and intraplate volcanoes in Northeast Asia, depicted as black triangles, with major plate boundaries. Modified from Kim et al. (2015).

Northeast Asia may be one of the best natural laboratories to investigate both arc and intraplate volcanisms which have developed since the mid-Miocene. The arc volcanoes have occurred above the sinking young (Philippine) and old (Pacific) oceanic plates in Southwest and Northeast Japan subduction zones, respectively. The intraplate volcanoes across the Korean Peninsula and China have occurred abo ...[Read More]

Application of lubrication theory in understanding subduction interface dynamics

August 3, 2022
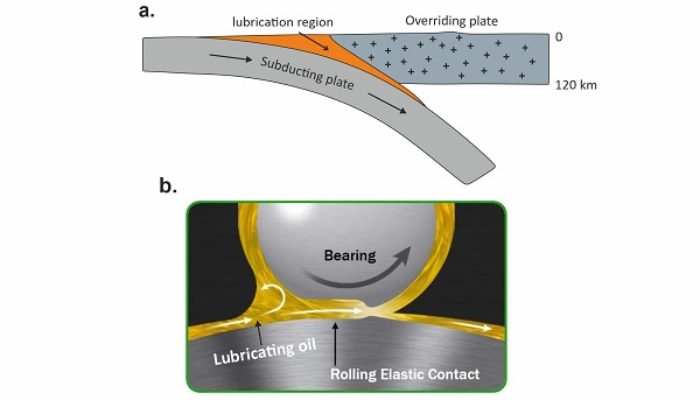
Application of lubrication theory in understanding subduction interface dynamics
Figure 1. Analogy of a) subduction interface with b) engineering lubrication device (source: machinerylubrication.com).

Plate interface lubrication is essential for stabilization and continuation of subduction process for million of years. The magnitude of plate interface lubrication determines transfer of stress between two converging plates, topography of mountain belts, transportation of volatiles to the mantle, and return flow of high to ultra-high pressure rocks to the earth’s surface.  In this week’s blog, I ...[Read More]

Journey of the Indian plate

March 30, 2022
Journey of the Indian plate
From the top of one of the largest monoliths in the Southern Indian craton | PC: Samik Sadhu | https://samiksadhu.weebly.com

Plume craton interaction is a fascinating geological phenomenon. The Indian plate, which has experienced several plume eruptions underneath it, is one of the best locations to study the effect of plume craton interaction. In this week’s news and view, I will provide an overview of the controversy and hypotheses related to the plume craton interaction within the Indian plate since the mid-Cre ...[Read More]

Orphaning: Discovering New Subduction Processes

and November 24, 2021
Orphaning: Discovering New Subduction Processes
Figure 1: P-Wave tomography by Obayashi et al. (2013) and Fukao & Obayashi (2013) for Tonga. Note the deflected slab at 660 km depth underlain by deeper slab material, possibly orphan slabs.

Science is all about discovering new things. But how do we make these discoveries, adding to the ever growing pantheon of knowledge? This week, we sit with one of our editors Antoniette Greta Grima, a Postdoctoral Fellow from the University of Texas at Austin, to understand what it takes to discover a new slab process.  Thanks for sitting down with us this week! First things first, which subductio ...[Read More]