The central Mediterranean is a geodynamically complex region shaped by the interaction of multiple active subduction zones. In Italy, the central Apennines display a distinctive pattern of surface deformation that is proposed to be linked to a slab break-off beneath the area. In this week’s blog post, Maaike, a PhD student at ISTerre in Grenoble, …[Read More]
Earth’s sister, Venus, is a planet whose evolution is drastically different from our own. Unravelling the hidden mysteries behind the divergent evolution of these two planets could hold the key to understanding what makes a planet habitable. Using numerical modelling, Diogo Lourenço and Cédric Gillmann unveil the dynamics of Venus while linking them to observations. …[Read More]
Subduction zones are dynamic regions where intense geological processes like earthquakes, volcanic eruptions, and the recycling of oceanic crust are constantly at play. A key factor that influences the behavior of these zones is *interface rheology*—the strength and viscosity of the boundary (the interface) between the subducting and overriding plates. Understanding this interface is crucial …[Read More]
Geodynamic modelling helps us understand Earth’s internal processes by providing a framework to test hypotheses. Analogue modelling uses physical models governed by the laws of nature, with resolution down to Planck’s length. In contrast, numerical modelling employs mathematical methods to approximate solutions to the physical laws governing Earth’s processes. Each modelling approach comes with its …[Read More]
All models are wrong, but some are useful – we all have heard this quote. But it raises several questions (including but not limited to) – What would a model of the entire world look like? Can you couple geodynamical models with climate and biological evolution models? Would these models be useful? In this week’s …[Read More]
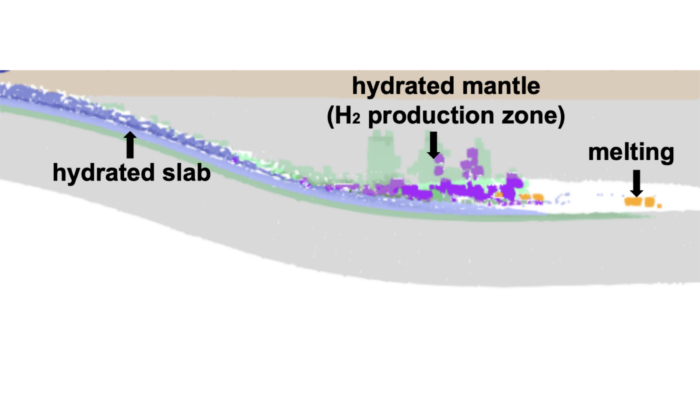
Dihydrogen (H2) is a promising source of energy that may allow reducing carbon emissions in industry and transportation. Artificial production methods have been explored, natural sources of H2 (also called white dihydrogen) offer a more eco-friendly and cost-effective production process. In this week’s blog post, Alexis Gauthier, a PhD student from ISTeP, France, is discussing …[Read More]
Geoscientists explore the nature from a different perspective than the commoners. In this week’s blog, Stephanie Sparks from Arizona State University shares her story how her passion for mountains gradually became her profession. Her journey through different regions in Himalaya leads her to understand the exhumation rate and the underlying geodynamic processes behind the formation …[Read More]
Within the vast realm of geoscience, the intricate mechanisms governing Earth’s internal processes continually pose challenges for researchers attempting to unveil its mysteries. This blog post acknowledges the inherent limitations of geological and geophysical data while highlighting the important role that geodynamic modeling plays in bridging these datasets. The motivations for this discussion arise from …[Read More]
A voyage between different tectonic modelling worlds: from sandbox to supercomputer
