Plate interface lubrication is essential for stabilization and continuation of subduction process for million of years. The magnitude of plate interface lubrication determines transfer of stress between two converging plates, topography of mountain belts, transportation of volatiles to the mantle, and return flow of high to ultra-high pressure rocks to the earth’s surface. In this week’s blog, I will discuss how lubrication theory from hydrodynamics can give us important insights in those aforementioned subduction zone processes.
Basic premise of subduction interface lubrication
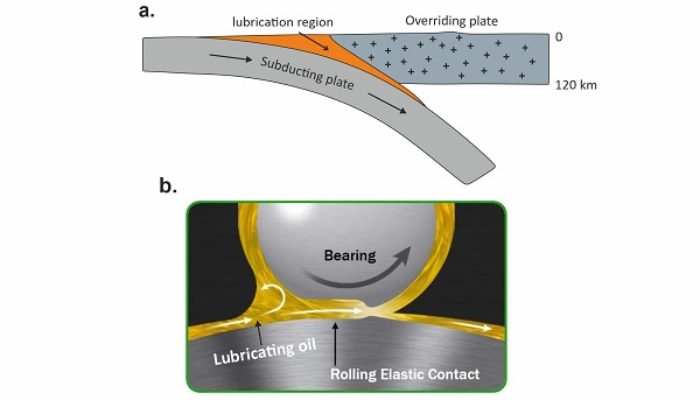
The subduction interface, where two colliding plates meet, displays a downward tapering geometry (i.e., wedge), often extending into a narrow conduit, called subduction channel (Fig. 1a). The interface is filled with sediments and crushed fragments of crustal rocks, derived from both subducting and overriding plates. The presence of fine grained wet sediments that preserve highly pressurized pore fluids provide low shear strength to the interface at shallower depth. With increasing depth the structurally bound fluid is partially released by successive dehydration reactions that further reduce the interface strength (Sobolev & Brown, 2019). Thus, the presence of sediments and metasedimentary rocks significantly contribute in lubricating the subduction interface along its full length. A number of studies have demonstrated how sediment subduction and resulting lubrication of the interface may influence plate velocities, large scale subduction dynamics, stabilization of long term subduction process and the development of present-day plate tectonics on Earth (Behr & Becker 2018; Sobolev & Brown, 2019; Chen et al., 2022). Apart from facilitating the downgoing motion of the subducting plate, the interface also controls a wide range geological processes which include metamorphism, exhumation of high to ultra-high pressure (i.e., deep-crustal) rocks, transfer of stress to upper plate, mountain uplift and topography development (Maiti et al., 2020). Using lubrication theory from hydrodynamics, here I discuss how the strength of the interface (i.e., effective viscosity) and its geometry can influence those above- mentioned geological processes.
Due to the presence of wet sediments and crustal fragments, as mentioned earlier, rocks in the subduction wedge and channel generally have lower viscosity (1019–1020 Pa s) and density (2500–3100 kg/m3) compared to the colliding lithospheric plates (1021–1023 Pa s and 2800–3250 kg/m3). Such a system is mechanically analogues to engineering thrust or pad bearing devices (Fig. 1b; Hamrock, 1991), in which two inclined plates remain separated by a low-density viscous wedge (Figs. 1b, 2a). The upper load-bearing plate is held stationary, whereas the lower plate moves at a tangential velocity and produces a flow-induced dynamic pressure (PDy) in the intervening viscous wedge. The PDy supports the load of the upper plate and keeps the two plates separated from each other. PDy is calculated using lubrication approximation (Hamrock, 1991), where the flow of fluid is considered dominantly plate parallel and the flow component across the plate is considered negligibly small. To satisfy these conditions it requires a low convergence angle (α < 1°) for hydrodynamic flows in engineering applications. However, considering extremely slow crustal or mantle flow velocity in the order of mm to cm/yr and viscosity more than 1019 Pa s, the lubrication theory can be effectively used in calculating dynamic pressure in subduction wedges with large convergence angle (e.g., α =25°; Maiti & Mandal, 2020).
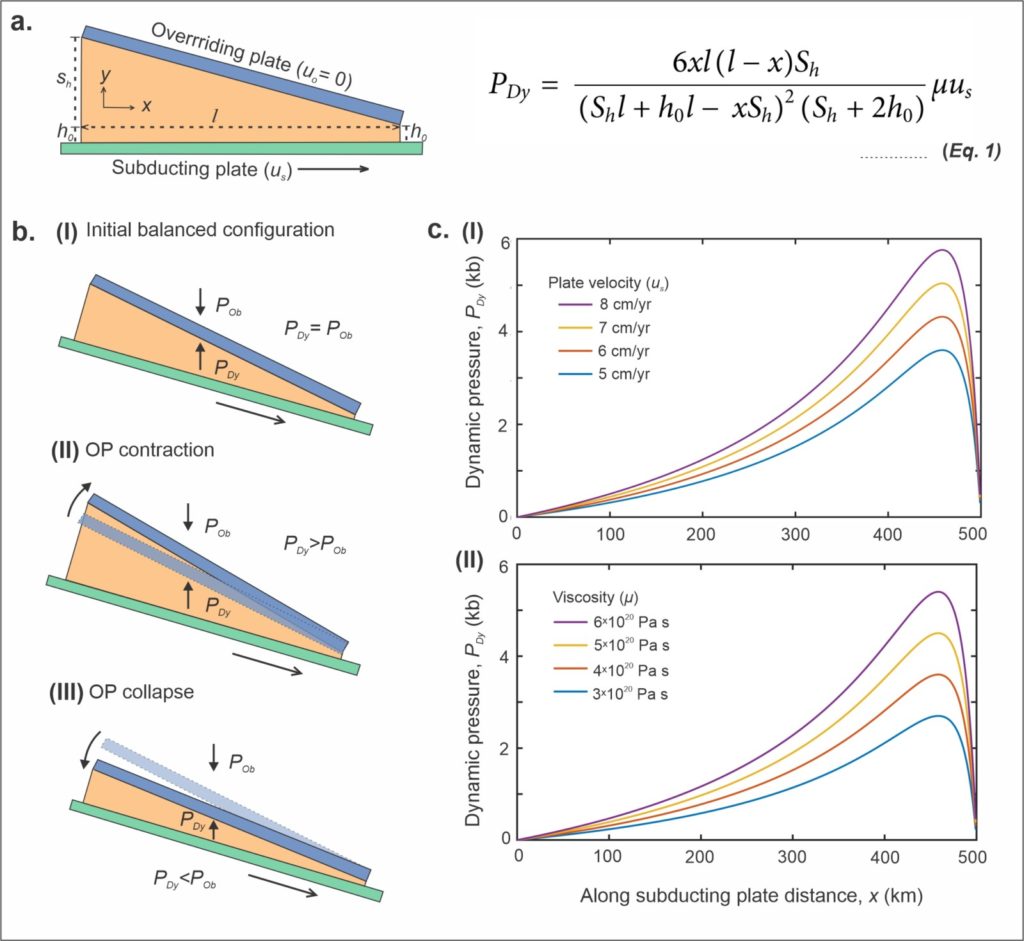
Figure 2. a) Geometrical parameters of subduction interface considered for the analysis of dynamic pressure, where h0 and (h0 + Sh) are the opening widths at the two converging ends of the interface, l is the along-plate length of the interface. The overriding plate is kept stationary (uo = 0) and the subducting plate moves at velocity us (cm/yr). b) Three dynamic states of a subduction interface system. I: dynamic pressure (PDy) equals to overburden pressure (POb), acting on the plate interface; the system is in a balanced state. II: PDy>POb; the overriding plate (OP) undergoes contractional deformation. III. PDy<POb; the OP undergoes rotational collapse. c) Graphical plots of PDy as a function of I) subduction plate velocity (us) and II) wedge viscosity (µ). Source: Maiti and Mandal, 2021.
Calculation of dynamic pressure
For a given tapered geometry of the viscous wedge (Fig. 2a), the dynamic pressure (PDy) is obtained from Reynold’s equation as a function of subducting plate velocity (us), and wedge viscosity (µ), where h0 and (h0 + Sh) are the opening widths at the two converging ends of the wedge, l is the along-plate wedge length (Maiti & Mandal, 2020). Eq. 1 shows that PDy holds a positive linear relation with us and μ (Fig. 2c). The lubrication dynamics suggests that the subducting plate motion develops a dynamic pressure (PDy) in the viscous wedge (Hamrock, 1991; Maiti & Mandal, 2020), which supports the excess gravitational load of the overriding plate (POb) and maintains an equlibrium state (PDy = POb) (Fig. 2b-i). In case PDy > POb, the system tends to achieve the equilibrium either by increasing the inter-plate distance and/or by transferring compressive stresses into the overriding plate (Fig. 2b-ii). In contrast, when PDy < POb, the system would reduce the inter-plate distance to raise the dynamic pressure level (closer the plates are, higher the friction and thereby higher dynamics pressure it creates) in order to restore the equlibrium state (Fig. 2b-iii). This condition triggers a gravitational collapse of the overriding plate onto the wedge and forces the buoyant wedge rocks to extrude out of the plate confinement zone.
However, lubrication theory considers a viscous wedge confined by rigid plates. But, in natural subduction zones the overriding and subducting plates are not entirely rigid and undergo significant deformation. Therefore, to study the effects of the key parameters (i.e., effective wedge viscosity and subduction velocity) obtained from lubrication theory, Maiti and Mandal (2020) conducted numerical simulations with deformable plates and performed a quantitative analysis for the stable to unstable transition of the overriding plate as a function of dynamic pressure. Their numerical results show that when PDy > POb the subducting slab drags the crustal materials deep into the wedge and a contractional deformation dominates in the overridng plate (Figs. 3a, c). However, when PDy < POb the burial of crustal rocks is replaced by extrusion of high pressure (HP) to ultra-high pressure (UHP) rocks and simultaneous extensional deformation in the overriding plate (Figs. 3b, c).
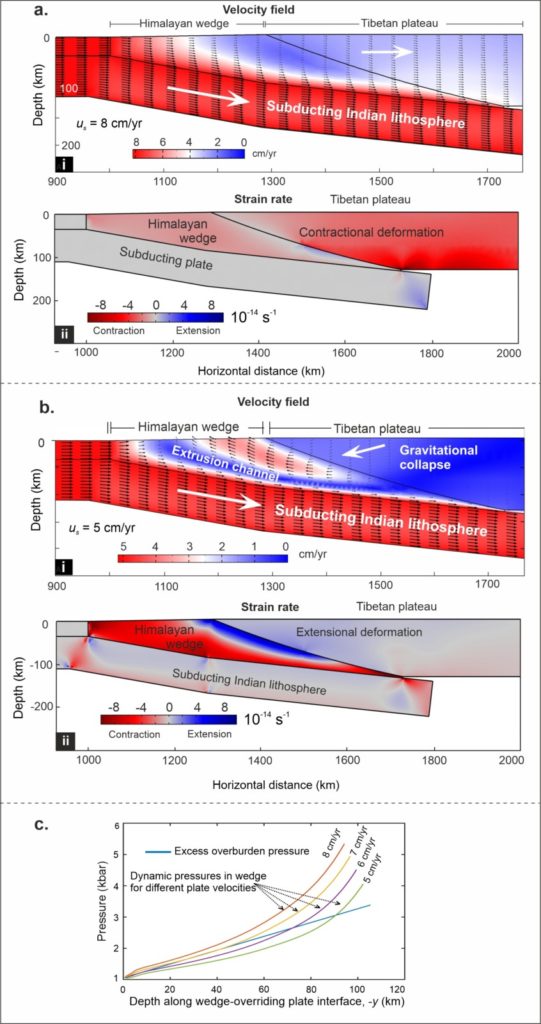
Figure 3. a) and b) show change in crustal flow pattern and corresponding strain rate in the Himalayan wedge and overriding Tibetan plateau, as subduction velocity drops from 8 to 5 cm/yr. Note that, when velocity drops to 5 cm/yr an upward extrusion channel starts forming in the wedge and overriding Tibetan plateau undergoes extensional deformation. c) Shows analysis of dynamics pressure in the wedge. For us = 5 cm/yr, PDy becomes significantly less than POb over a large part of the wedge, resulting in a fully developed large-scale extrusion zone within the wedge. Source: Maiti and Mandal, 2021
Geological processes causing drop in dynamic pressure
From analytical and numerical model results of lubrication dynamics, we find that a critical drop in wedge viscosity (µ) and/or plate velocity (us) can cause drop in dynamic pressure below the overburden pressure, which in turn causes extrusion of buyoant rocks from the wedge/subduction channel and triggers gravitational collapse of the overriding plate (Fig.3; Maiti et al., 2020; Maiti & Mandal, 2021). A number of geological factors can reduce viscosity of wedge/subduction channel rocks. These include volatile release from subducting plate, presence of partial melts, and strain weakening. In many continental as well as oceanic HP and UHP terranes, eclogites are found to be associated with serpentinite matrix. Serpentinitization associated with volatile release from the subducting plate can be a potential viscosity-reducing mechanism and also act as a buoyancy enhancing agent. Moreover, high pressure -temperature experiments indicate that dehydration melting can also dramatically change the viscosity in subduction channel, where partial melting only in a few percent (~7 %) reduces the viscosity of crustal rocks by about 90% (Rosenberg & Handy, 2005). The possibility of such melt -induced viscosity drop and their possible role in exhumation is suggested from extensive migmatization in many continental UHP terranes, such as Western Gneiss Region in Norway, Woodlark Basin, Dabie Sulu region, Kokchetav Massif, Greenland Caledonide (Maiti & Mandal, 2020 and references therin).
Subduction velocity drop can be another critical factor in reducing dynamic pressure as suggested by lubrication theory. Geological processes that can cause significant subduction velocity drop include removal of load through delamination of lower crust or decoupling/breakoff of oceanic lithosphere from the lighter continental lithosphere during continental collision (von Blackenburg & Davies, 1995; Agard et al., 2009). In a number of HP and UHP terranes, such as European Alps (von Blackenburg & Davies, 1995), Timor and Seram region of eastern most Java trench (Ernst et al., 1997), western gneiss complex in Norwegian Caledonides (Brueckner and Cuthbert, 2013) slab breakoff event is found to be coeval with deep-crustal exhumation timing. Recently, Maiti and Mandal (2021) showed that a critical drop in India-Asia convergence velocity played an important role in initiation of ductile extrusion of higher Himalayan crystalline and a coeval gravitational collapse of the overriding Tibetan plateau (Fig. 3).
References. Agard, P., Yamato, P., Jolivet, L., Burov, E. (2009). Exhumation of oceanic blueschists and eclogites in subduction zones: timing and mechanisms. Earth-Science Rev. 92, 53–79. doi:10.1016/j.earscirev.2008.11.002 Ernst, W.G., Maruyama, S., Wallis, S. (1997). Buoyancy-driven, rapid exhumation of ultrahigh-pressure metamorphosed continental crust. Proc. Natl. Acad. Sci. 94, 9532–9537. https://doi.org/10.1073/pnas.94.18.9532. Behr, W.M. & Becker, T.W., (2018). Sediment control on subduction plate speeds, Earth planet. Sci. Lett., 502, 166–173 von Blackenburg, F., and Davies, H.J. (1995). Slab breakoff: a model for syncollisional magmatism. Tectonics 14, 120–131. Brueckner, H.K., and Cuthbert, S.J. (2013). Extension, disruption, and translation of an orogenic wedge by exhumation of large ultrahigh-pressure terranes: examples from the Norwegian Caledonides. Lithosphere 5, 277–289. doi:10.1130/l256.1. Chen, G., Cheng, Q., Peters, S.E., Spencer, C.J. & Zhao, M. (2022). Feedback between surface and deep processes: insight from time series analysis of sedimentary record, Earth planet. Sci. Lett., 579, doi:10.1016/j.epsl.2021.117352 Hamrock, B. J. (1991). Fundamentals of fluid film lubrication, NASA Ref. Publ., 1255, 670,doi:10.1201/9780203021187. Maiti, G., and Mandal, N. (2020). How far does a subduction wedge follow lubrication dynamics? Phys. Earth Planet. Interiors 298, 106346. doi:10.1016/ j.pepi.2019.106346. Maiti, G., and Mandal, N. (2021). Early Miocene Exhumation of High-Pressure Rocks in the Himalaya: A Response to Reduced India-Asia Convergence Velocity. Front. Earth Sci. 9:632806. doi: 10.3389/feart.2021.632806. Maiti, G., Mandal, N., & Misra, S. (2020). Insights into the dynamics of an orogenic wedge from lubrication theory: Implications for the Himalayan tectonics. Tectonophysics, 776, 228335. https://doi.org/10.1016/j.tecto.2020.228335. Rosenberg, C.L., and Handy, M.R. (2005). Experimental deformation of partially melted granite revisited: implications for the continental crust. J. Metamorph. Geol. 23, 19–28. doi:10.1111/j.1525-1314.2005.00555.x. Sobolev, S.V., and Brown, M. (2019). Surface erosion events controlled the evolution of plate tectonics on earth, Nature, 570(7759), 52–57




