The Earth, with its towering mountains, shifting tectonic plates, and dynamic geological processes, has always been a subject of fascination and inquiry for scientists. Amidst the vast array of scientific disciplines, one relatively small yet impactful field, known as experimental rock deformation, plays a crucial role in unraveling the mysteries hidden beneath the Earth’s surface. Though the number of experimentalists is modest, the implications of their work extend far beyond the laboratory, influencing a myriad of scientific applications. This discipline revolves around comprehending mechanical and chemical processes involving deformation across a vast spectrum of temperatures, pressures, and timescales. In this week’s blog post, Subhajit, a specialist in rock deformation experimentation, will explore the importance, scientific principles, and various methods of rock deformation experiments. The blog ends with his introduction to the latest advancements in this field, highlighting their implications in enhancing our understanding of the long-term rheological behavior of Earth’s crust.

Subhajit Ghosh is a rock deformation experimentalist. Presently, he is working as a post-doc at Woods Hole Oceanographic Institution (WHOI) and exploring the strength of the oceanic crust, specifically focusing on plagioclase and pyroxene paleo-piezometers.
From the surface of the Earth to its profound depths and even to other planets, scientists, guided by the principles of materials science, delve into the mysteries of minerals, rocks and ice. For instance, a field geologist measures recrystallised grain sizes through microscopic study, deriving insights to determine paleo stress states. Meanwhile, a geodynamicist seeks realistic mathematical equations (flow laws) to understand long-term flow behaviour of Earth’s crust and mantle through numerical modelling. However, the field of experimental rock deformation isn’t confined to labs and theories; it has real-world applications. Picture a seismologist looking for precursor signs to predict earthquakes or a hydrogeologist assessing the integrity of an aquifer or an engineer monitoring pressure changes associated with waste disposal. The applications are diverse and touch on numerous aspects of our lives, from earthquake risk assessment to extracting energy safely to urban planning for rising sea levels.
In the quest to constrain properties of geological or planetary materials or rocks, information from dominant mineral phases become essential. For instance, quartz and feldspar rheology are important to model the (mid and lower) crustal, while olivine rheology is important to model the mantle processes. Experimentalists adopt two approaches for subsequent laboratory deformation: 1) creating synthetic rock samples in the lab (Ghosh et al., 2021), or 2) collecting natural rock samples from the field. Afterwards, the data collection process involves recording stress (force), and strain (displacement) data, under varying confining pressures, temperatures and hydrous conditions. The results are then fitted into an equation involving the strain rate (˚ε), a dimensionless constant (A), the activation energy for creep (Q), the gas constant (R), absolute temperature (T), differential stress (σ), grain size (d), the water fugacity term with an exponent (r), stress exponent (n), and grain size exponent (p):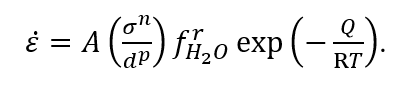 Once such a equation (also known as flow law) is established, the lab results can be extraprolated to the natural conditions to model or predict the mechanical behavior of the geological materials. Moreover, the flow law parameters are good indicators of grain scale deformation mechanisms. Theoretical models of the creep have shown different values of n and p for different creep mechanisms. For example, n = 1 and p = 2 or 3 indicate lattice diffusion (Nabarro-Herring) creep or grain boundary diffusion (Coble) creep (Nabbaro, 1948; Herring, 1950; Coble, 1963), respectively. On the other hand, n ≥ 3 and p = 0 generally correspond to the dislocation creep process. Nonetheless, by identifying grain-scale deformation processes through careful microstructural characterization and quantifying their dependencies on time, stresses, temperatures and pressures, scientists bridge the gap from the laboratory scale to understanding Earth at large.
Once such a equation (also known as flow law) is established, the lab results can be extraprolated to the natural conditions to model or predict the mechanical behavior of the geological materials. Moreover, the flow law parameters are good indicators of grain scale deformation mechanisms. Theoretical models of the creep have shown different values of n and p for different creep mechanisms. For example, n = 1 and p = 2 or 3 indicate lattice diffusion (Nabarro-Herring) creep or grain boundary diffusion (Coble) creep (Nabbaro, 1948; Herring, 1950; Coble, 1963), respectively. On the other hand, n ≥ 3 and p = 0 generally correspond to the dislocation creep process. Nonetheless, by identifying grain-scale deformation processes through careful microstructural characterization and quantifying their dependencies on time, stresses, temperatures and pressures, scientists bridge the gap from the laboratory scale to understanding Earth at large.
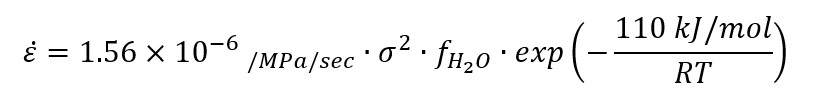 Interestingly, these results deviate from the expected predictions of climb-accommodated dislocation creep models with n ≈ 3-5 (e.g., Hirth et al., 2001). The microstructural analysis suggests that the bulk sample strain in those experiments is achieved by crystal plasticity (Nègre et al., 2021), i.e., dislocation glide with minor recovery by recrystallisation and sub-grain rotation, accompanied by grain boundary migration (GBM) (Ghosh et al., 2022). In addition to dynamic recrystallization, micro-cracking helps to nucleate new grains (see figures in Nègre et al., 2021; Pongrac et al., 2022).
Interestingly, these results deviate from the expected predictions of climb-accommodated dislocation creep models with n ≈ 3-5 (e.g., Hirth et al., 2001). The microstructural analysis suggests that the bulk sample strain in those experiments is achieved by crystal plasticity (Nègre et al., 2021), i.e., dislocation glide with minor recovery by recrystallisation and sub-grain rotation, accompanied by grain boundary migration (GBM) (Ghosh et al., 2022). In addition to dynamic recrystallization, micro-cracking helps to nucleate new grains (see figures in Nègre et al., 2021; Pongrac et al., 2022).

[The figures (Cathodoluminescence (CL) image and EBSD orientation map) are taken from Nègre et al. (2021). The recrystallized grains and subgrains are clearly visible in the EBSD map. The CL image shows lighter luminescent materials along the grain boundary regions of larger grains, highlighting recrystallized areas. Some of these new grains contain a CL-dark (original luminescence) fragments, preserving their angular shape, revealing their origin due to cracking (circles on the maps). These cracked grains then grew (indicating the activity of GBM) during the experimental time-scale with a lighter CL luminescence. The undulatory grain boundary indicating GBM can also be recognized with a lighter CL luminescence (boxes on the maps). This information is missing in the EBSD map.]
In essence, experimental rock deformation serves as an invaluable tool for unraveling the mysteries of our planet’s geological processes. As technology advances and our understanding deepens, experimental rock deformation will continue to serve as a beacon, illuminating the pathways to understanding the Earth’s inner workings.
References:
https://structuredatabase.wordpress.com/deformation-apparatus/ https://eos.org/opinions/laboratory-sharing-to-improve-rock-deformation-research OpenAI. ChatGPT (3.5). Retrieved from https://openai.com/chatgpt Coble, R.L., 1963. A model for boundary diffusion controlled creep in polycrystalline materials. J Appl Phys 34, 1679–1682. Griggs, D. J. Hydrolytic weakening of quartz and other silicates. Geophys. J. Int. 14(1-4), 19 – 31, doi:10.1111/j.1365-246X.1967.tb06218.x (1967). Green, H. W., and Borch, R. S. A New Molten Salt Cell for Precision Stress Measurements at High Pressure. Eur. J. Mineral. 1(2), 213 – 219, doi:10.1127/ejm/1/2/0213 (1989). Ghosh, S., Koizumi, S., Hiraga, T., 2021. Diffusion Creep of Diopside. J Geophys Res Solid Earth 126. https://doi.org/10.1029/2020JB019855 Ghosh, S., Stünitz, H., Raimbourg, H., Précigout, J., 2022. Quartz rheology constrained from constant-load experiments: Consequences for the strength of the continental crust. Earth Planet Sci Lett 117814. https://doi.org/10.1016/j.epsl.2022.117814 Ghosh, S., Mandal, N., Roy, S., Bose, S., 2023. Tectono-metamorphic transitions in the higher Himalayan sequence: A clue for Main Central Thrust (MCT) localization in Darjeeling-Sikkim Himalaya. Journal of Structural Geology, 167 (2023) 104783. https://doi.org/10.1016/j.jsg.2022.104783 Herring, C., 1950. Diffusional viscosity of a polycrystalline solid. J Appl Phys 21, 437–445. Hirth, G., Teyssier, C., Dunlap, W.J., 2001. An evaluation of quartzite flow laws based on comparisons between experimentally and naturally deformed rocks. International Journal of Earth Sciences 90, 77–87. https://doi.org/10.1007/s005310000152 Nabbarro, F.R.N., 1948. Deformation of crystals by motion of single ions, in: Report on a Conference on the Strength of Solids. The Physical Society. Nègre, L., Stünitz, H., Raimbourg, H., Lee, A., Précigout, J., Pongrac, P., Jeřábek, P., 2021. Effect of pressure on the deformation of quartz aggregates in the presence of H2O. J Struct Geol 148. https://doi.org/10.1016/j.jsg.2021.104351 Pongrac, P., Jeřábek, P., Stünitz, H., Raimbourg, H., Heilbronner, R., Racek, M., Nègre, L., 2022. Mechanical properties and recrystallization of quartz in presence of H2O: Combination of cracking, subgrain rotation and dissolution-precipitation processes. J Struct Geol 160. https://doi.org/10.1016/j.jsg.2022.104630 Précigout, J., Stünitz, H., Pinquier, Y., Champallier, R., Schubnel, A., 2018. High-pressure, high-temperature deformation experiment using the new generation griggs-type apparatus. Journal of Visualized Experiments 2018. https://doi.org/10.3791/56841 Scholz, C., 1998. Earthquakes and friction laws. Nature 391, 37–42. Tullis, T. E., et al. (2013), Advancing experimental rock deformation research: Scientific, personnel, and technical needs, white paper, 85 pp., Div. of Earth Sci., Natl. Sci. Found., http://espm.wustl.edu/files/2016/11/Tullis-et-al-2012-Experimental-Rock-Deformation-23yyaqp.pdf.