rheology

Exploring rheology of Earth’s materials: The marvels of high-temperature high-pressure deformation experiments

Subhajit Ghosh and edited by Giridas Maiti May 1, 2024

[Mylonitization in quartz rich rocks from Himalayan shear zone, from Ghosh et al., 2023]

The Earth, with its towering mountains, shifting tectonic plates, and dynamic geological processes, has always been a subject of fascination and inquiry for scientists. Amidst the vast array of scientific disciplines, one relatively small yet impactful field, known as experimental rock deformation, plays a crucial role in unraveling the mysteries hidden beneath the Earth’s surface. Though th ...[Read More]

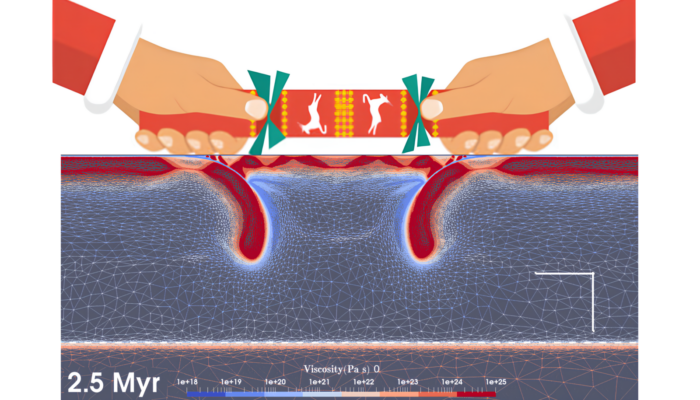
Dual inward dipping subduction: A Christmas Cracker Model

edited by Zhibin Lei September 27, 2023

A recent research finds that dual inward dipping subduction framework, after considering thermal dependent deformation mechanisms, can pull apart the middle overriding plate (Lei and Davies, 2023), just like pulling Christmas crackers from both ends! Dual inward dipping subduction (DIDS) occurs when the overriding plate is decoupled with two subducting slabs dipping towards each other. DIDS is fou ...[Read More]

Geodynamics 101 – Viscous anisotropy

Ágnes Király March 16, 2023

We are living in an anisotropic world. From rock-building crystals, ice, and trees growing in your garden to your favourite slice of cake many materials or objects has some anisotropic behaviour. What does this mean? Anisotropy (non-isotropy) implies that a material property depends on the direction of the measurement. In geodynamics we often talk about seismic anisotropy, originating from microsc ...[Read More]

The Sassy Scientist – Rock-‘N’-Roll

The Sassy Scientist June 12, 2020

Aïda rummages around within the lavish ball pit of rock samples as often as not, but is left unsure which rock type should be her number one: What is your favourite rock? Dear Aïda, I’ll be honest with you. Yeah, I’m surprised too… I don’t occupy myself that often with constructing countdown lists of rock types, and simply consider all rocks as equally and most important. O ...[Read More]