Rayleigh-Taylor instability in geodynamics

Flow against gravity is a common feature in the geodynamic phenomenon. In this week’s Geodynamics 101, Dip Ghosh from Jadavpur University Geodynamics Lab will explain the fundamentals of Rayleigh-Taylor instability: A key to understanding the anti-gravity flow.

It has long been realized that most of the geodynamic processes can be described in terms of slow viscous flow. Thus, like many other fields of earth and planetary sciences, geodynamics too owes a lot to fluid mechanics. In fact, two of the three basic equations of numerical geodynamics happen to be the fundamental equations of fluid mechanics, i.e., the continuity equation and the Navier-Stokes equation. Despite their inherent non-linearity and complexity, these equations may lead to stationary solutions for a specific set of parameters. Beyond this, the system cannot sustain itself against a small mode of perturbation due to its inherent instability (Chandrasekhar, 1961). One such instability of particular interest in geodynamics is Rayleigh-Taylor instability due to its ubiquitous occurrence in the dynamic Earth.

What is Rayleigh-Taylor instability?

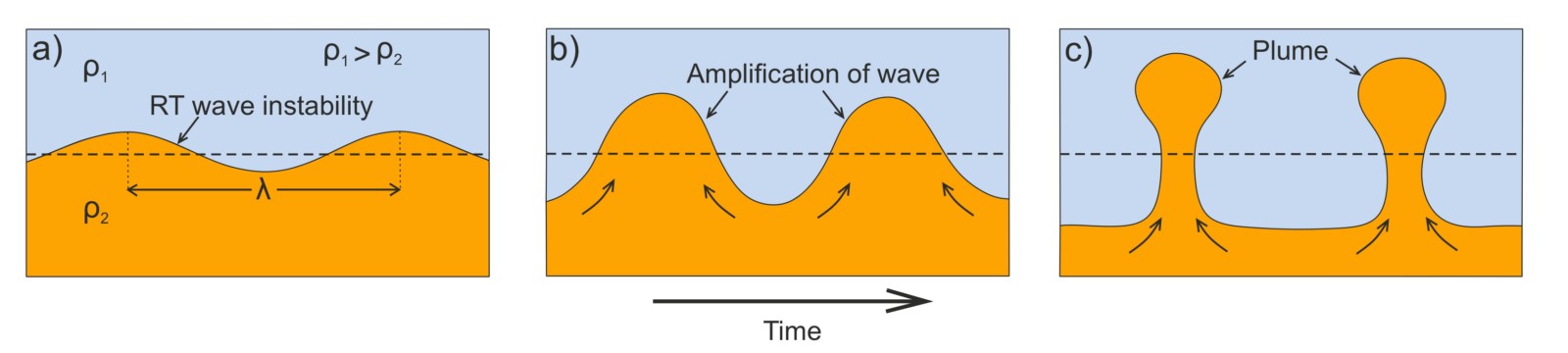
Figure 1. A cartoon presentation of Rayleigh-Taylor instability at the interface between two fluid layers of contrasting densities (ρ), leading to plume formation. λ: wavelength of the instability.

Inversion in density stratification develops gravitational instability at the interface between two fluids of contrasting densities, where the relatively low-density fluid pushes the overlying denser fluid (Taylor, 1950). This kind of instability termed Rayleigh–Taylor (RT) instability leads to the fingering of low-density fluids into the denser overburden (Fig. 1). If the interface between the underlying and the overburden is slightly distorted, a horizontal pressure gradient is created. And thus, a flow field will form, eventually amplifying the distorted interface to produce fully grown instabilities with finite amplitude.

The phenomenology of RT instability can be subdivided into 4 stages (Sharp, 1984). During the first stage, the growth of the interface would be exponential (Fig. 1a) and we can analyze it using linear dynamical equations i.e., the governing equations can be linearized. During stage 2, the instability development is strongly influenced by three-dimensional effects and we need to incorporate non-linearities to adequately describe the behaviour of the interface (Fig. 1b). The 3^rd stage is characterized by the development of mature “plumes” due to further nonlinear interaction of the unstable modes with other non-linear modes (Fig. 1c). The shape of the plume depends on the physical properties of the system such as viscosity ratio, density ratio and surface tension, or even the boundary condition of the system. During the final stage, turbulent mixing occurs and the whole structure breaks down.

In geodynamics, we can neglect inertial and surface tensional forces due to slow viscous nature of the flow dynamics. As a result, Reynold’s number for geodynamic processes is very low (Re ~ 0.1-1) and RT instabilities rarely show any turbulent mixing. The theory of RT instability has been extensively used to model several geodynamic processes. Some important ones are as follows:

1. Origin and growth of mantle plumes
2. Salt dynamics
3. Formation of intraplate orogeny
4. Core formation

To provide a general idea of RT instability in geodynamics, I’ll discuss some of these processes.

RT instability and mantle plumes

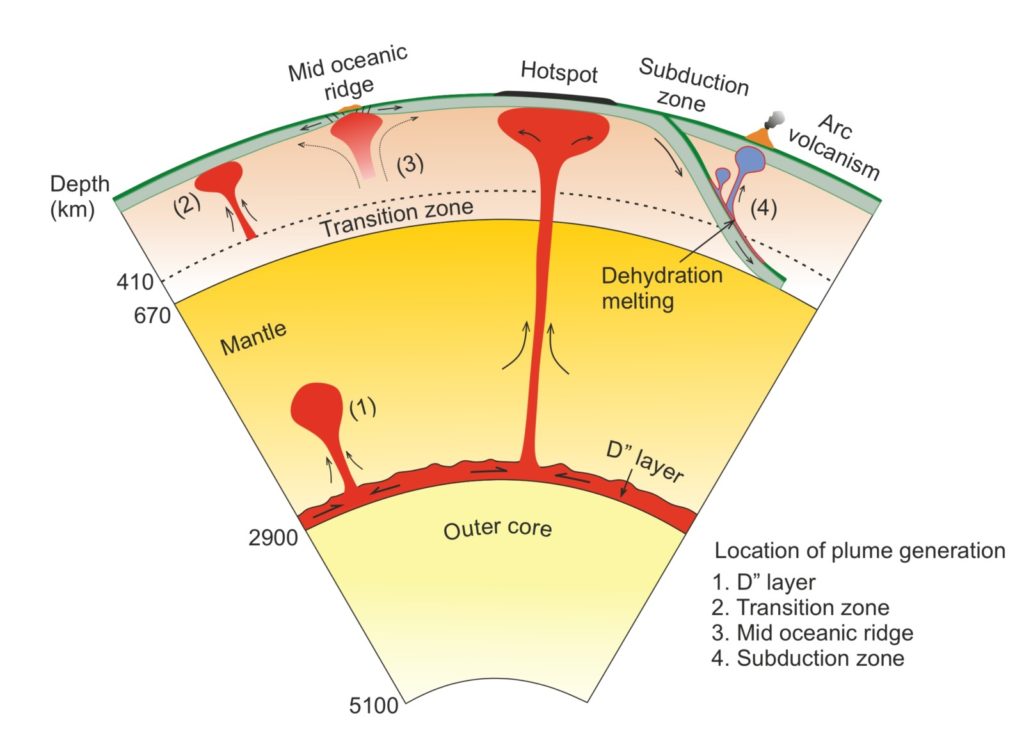
Figure 2. Prime geodynamic locations for plume generation inside the Earth.

Plumes can originate at different geodynamic locations within Earth’s mantle (Fig. 2), such as D” layer (core-mantle boundary) (Korenaga, 2005), transition zone (Cserepes and Yuen, 2000), and subduction wedge (Gerya and Yuen, 2003). The mantle plumes generated in D” layer are driven either by thermal or thermochemical forcing. It is shown via numerical studies that there is a marked difference in the structure and surface manifestation between the two. While classical thermal plume models indicate a large plume head with a narrow tail which corresponds to kilometer-scale surface uplift and a subsequent eruption of a large igneous province (LIP) (Farnetani and Richards, 1994), the thermomechanical low buoyancy plumes (LBPs) show much less prominent head and a much thicker tail which results in less pronounced surface uplift (~400 m) characteristic of typical LIP (Fig. 3b-e). These LBPs cross the density barrier present within the mantle either via mantle subadiabaticity or via high excess temperature (~550 K) within the plume (Dannberg and Sobolev, 2015) (Fig. 3a).

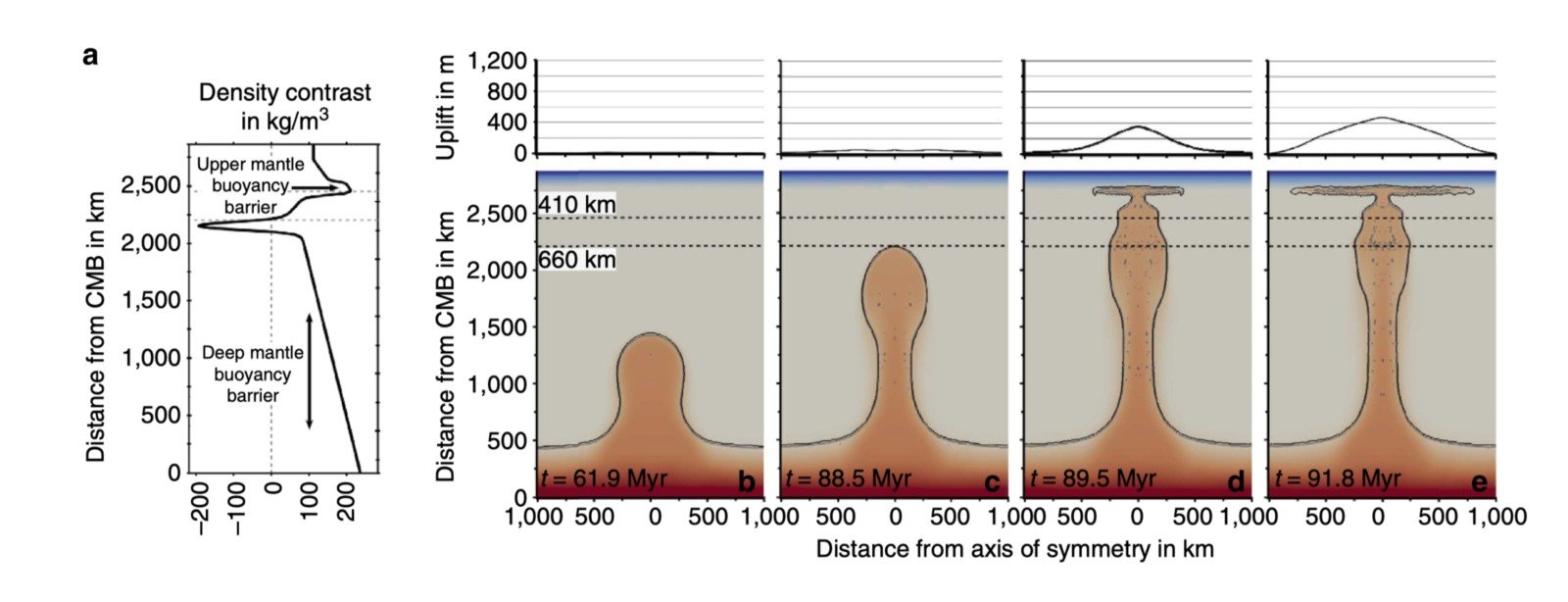
Figure 3. Evolution of LBPs in an adiabatic mantle along with corresponding surface upliftment as obtained from numerical experiments. Figure from Dannberg and Sobolev, 2015

Subduction plumes

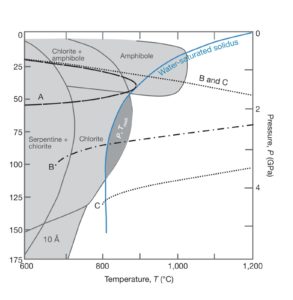
Figure 4. Phase diagram for hydrous peridotite. Figure obtained from Grove et. al., 2012.

Figure 5. Different patterns of cold plumes in the subduction zone as obtained from CFD simulations. Figure from Zhu et. al., 2009.

Subduction zones develop a specific geodynamic setting for RT instability to produce plumes in a relatively cold environment (Fig. 4). These ‘cold plumes’ are predicted to originate owing to compositional buoyancy attributed to partial melting due to fluids released by chlorite decomposition. Chlorite is stable above the H₂O-saturated solidus between 2 and 3.6 GPa and 800 to 820°C which corresponds to a depth of 50-150 km depending upon slab-dip. Since a fertile peridotite can stabilize up-to 7% chlorite, which in itself contains ~13 wt% H₂O; up-to 2 wt% bulk H₂O releases during chlorite decomposition (Grove et al., 2012). The structural water released from chlorite is enough to trigger the melting of the overlying mantle wedge. This melt, being less dense than the overlying mantle wedge forms RT instabilities and subsequent diapiric structures. Zhu et al., (2009) have shown from 3-D numerical simulations that slab dehydration sets in small-scale convection and cold plumes in the mantle wedge. Their simulations produce different types of plume patterns depending upon the viscosity of melt zones (Fig. 5). Recently it is shown that the different subduction plume patterns are a result of the interplay between two dominating mechanisms: 1) RT instabilities and 2) slab-dip parallel material advection (Ghosh et al., 2020). It was found that the inclination of the subducting slab is a major factor as they not only affect the thermal structure of the subduction zone, but they are also key to determining the dominant mechanism controlling the subduction plume dynamics. These patterns are extremely helpful as they provide insights into the final plume structure which, in turn, determines the distribution of volcanoes at the surface.

Salt tectonics and RT instability

Salt domes are another example of RT instability where the less dense evaporite beds intrude the overlying denser sedimentary rock strata. Initially, a layer of salt is deposited by evaporation of seawater in a restricted basin where there is an imbalance between basin inflow and outflow. Subsequent sedimentation buries this layer under other heavier clastics. With time, the density of the sediment layer increases due to compaction whereas, at greater depth, the density of the salt layer further decreases owing to an increased geothermal gradient. This creates an ideal condition for RT instability where salt layer starts to move upward by thermally activated creep processes and replace the overburden sedimentary strata. It is considered that syn-depositional salt movement is the key to allow further upward movement of the salt diapirs (Fig. 6).

Figure 6. Various stages of growth of salt diapirs as found in CFD simulation. Figure fromFernandez and Kaus, 2015.

Fernandez and Kaus, (2015) have shown that sedimentation rate and initial salt layer thickness are two major parameters that determine the ultimate 3-D geometry of the overall salt dome structure. They showed, via numerical modeling investigations that lower sedimentation rates result in more elongated salt exposures, whereas higher sedimentation rates result in more finger-like salt diapirs. For higher salt layer thickness, they have found that the spacing of the diapirs is more compared to that for low thickness. The salt also tends to flow much earlier for higher salt layer thickness.

Salt domes are important in petroleum geology because the deformation of the rocks above salt domes results in the formation of impermeable traps for the upward migrating oil and gas. Many oil and gas fields are associated with salt tectonics.

RT instability and intraplate orogeny

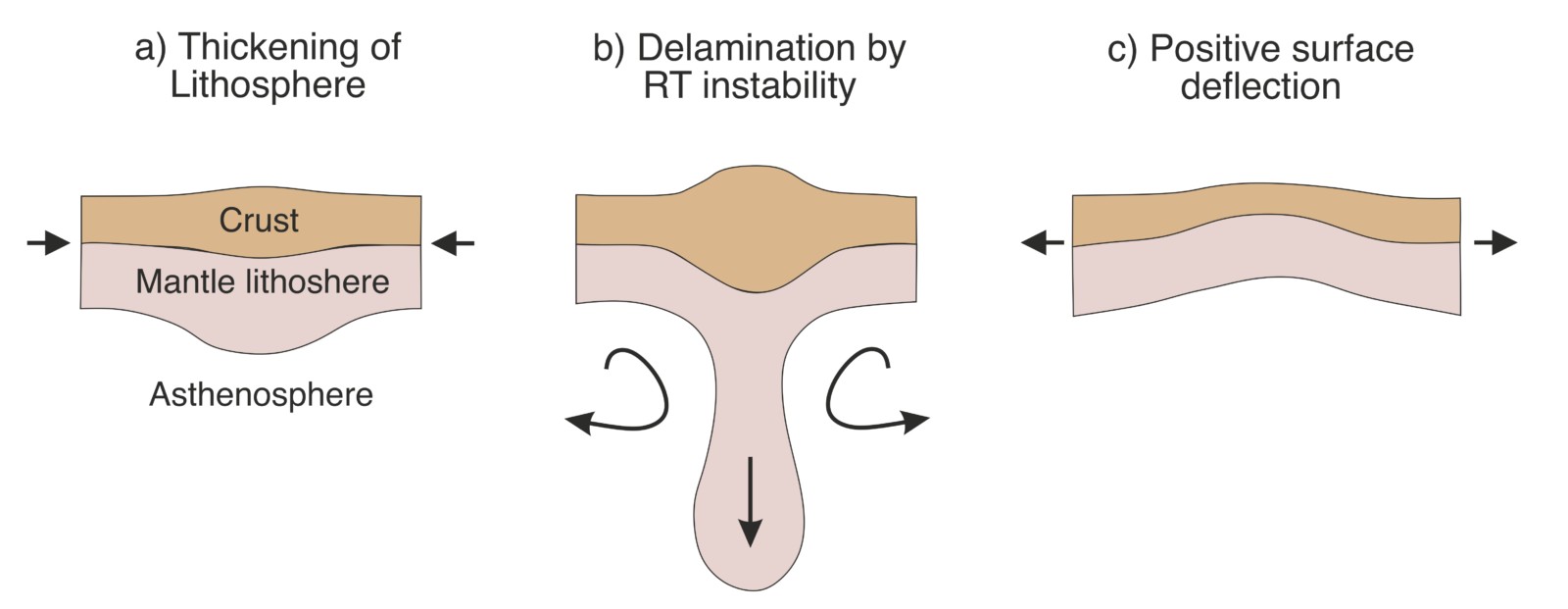
Figure 7. Cartoon diagram showing a mechanism of initiation of RT instabilities and corresponding orogeny in intra-continental settings. Figure modified from Gorczyk et al., 2012.

There are ample examples of large-scale orogenic upliftment events far from active tectonic margins throughout the geologic time. They are often attributed to delamination and subsequent RT instability within the sub-continental lithospheric mantle (SCLM) (Gorczyk et al., 2012; Gorczyk and Vogt, 2015). The general hypothesis states that the SCLMs underneath the old continents are very heterogeneous both compositionally and thermally (Neil and Houseman, 1999). Mechanical thickening of the crust due to far-field stress enables strain localization within the weak zones in SCLM (Fig. 7a). Due to this thickening of the crust, parts of SCLM reach the eclogite stability field and the resulting eclogitized crust now has a higher density than the underlying mantle. As a consequence, RT instability develops and the denser mantle lithosphere eventually gets delaminated into the deeper mantle (Fig. 7b, 8). Now that the crustal material is replaced by mantle material, and crust is now less dense, it can create intra-continental orogeny due to isostatic adjustments (Fig. 7c, 8).

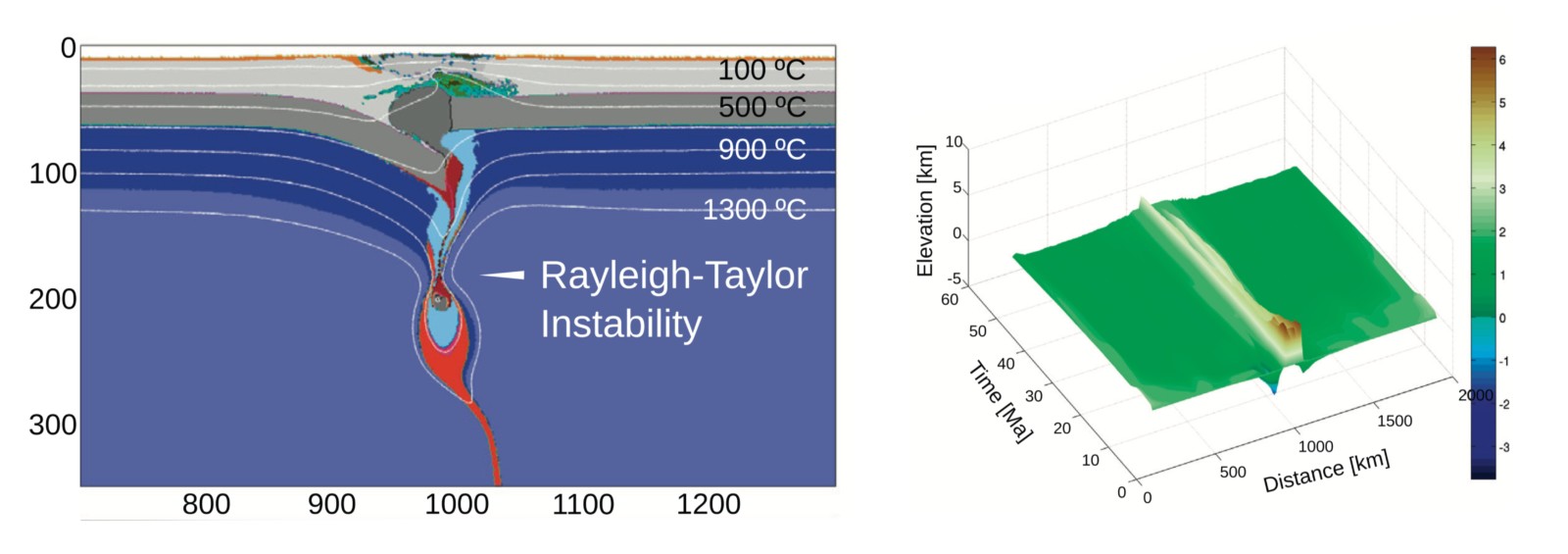
Figure 8. Numerical simulation showing the formation of gravitational instability and a corresponding increase in elevation. Figure modified from Gorczyk and Vogt, 2015.

We can use this concept to explain Archean oceanic crust dynamics and stagnant lid convection dynamics in other terrestrial planets (Mondal and Korenaga, 2018). Conrad and Molnar, (1997) proposed that gravitational instabilities and subsequent upliftment are the dominant mechanism for the present elevation of the Tibetan plateau.

Author’s note:  I think that a blog of this size cannot do justice to the immensity of the subject to its full potential. As a result, many parts of the subject could not get its attention as the other parts did. I hope that this blog and the references herein at least serves as a general introduction to one and all who wants to dive deeper into the subject.

References:

Chandrasekhar, S., 1961. Hydrodynamic and Hydromagnetic Stability.

Conrad, C.P., Molnar, P., 1997. The growth of Rayleigh-Taylor-type instabilities in the lithosphere for various rheological and density structures. Geophysical Journal International 129, 95–112. https://doi.org/10.1111/j.1365-246X.1997.tb00939.x

Cserepes, L., Yuen, D.A., 2000. On the possibility of a second kind of mantle plume. Earth and Planetary Science Letters 183, 61–71. https://doi.org/10.1016/S0012-821X(00)00265-X

Dannberg, J., Sobolev, S. V., 2015. Low-buoyancy thermochemical plumes resolve controversy of classical mantle plume concept. Nature Communications 6, 1–9. https://doi.org/10.1038/ncomms7960

Farnetani, C.G., Richards, M.A., 1994. Numerical investigations of the mantle plume initiation model for flood basalt events. Journal of Geophysical Research 99. https://doi.org/10.1029/94jb00649

Fernandez, N., Kaus, B.J.P., 2015. Pattern formation in 3-D numerical models of down-built diapirs initiated by a Rayleigh–Taylor instability. Geophysical Journal International 202, 1253–1270. https://doi.org/10.1093/gji/ggv219

Gerya, T., Yuen, D.A., 2003. Rayleigh - Taylor instabilities from hydration and melting propel “cold plumes” at subduction zones. Earth and Planetary Science Letters 212, 47–62. https://doi.org/10.1016/S0012-821X(03)00265-6

Ghosh, D., Maiti, G., Mandal, N., 2020. Slab-parallel advection versus Rayleigh-Taylor instabilities in melt-rich layers in subduction zones: A criticality analysis. Physics of the Earth and Planetary Interiors 307, 106560. https://doi.org/10.1016/j.pepi.2020.106560

Gorczyk, W., Hobbs, B., Gerya, T., 2012. Initiation of Rayleigh-Taylor instabilities in intra-cratonic settings. Tectonophysics 514–517, 146–155. https://doi.org/10.1016/j.tecto.2011.10.016

Gorczyk, W., Vogt, K., 2015. Tectonics and melting in intra-continental settings. Gondwana Research 27, 196–208. https://doi.org/10.1016/j.gr.2013.09.021

Grove, T., Till, C.B., Krawczynski, M.J., 2012. The Role of H2O in Subduction Zone Magmatism. Annual Review of Earth and Planetary Sciences 40, 413–439. https://doi.org/10.1146/annurev-earth-042711-105310

Korenaga, J., 2005. Firm mantle plumes and the nature of the core-mantle boundary region. Earth and Planetary Science Letters 232, 29–37. https://doi.org/10.1016/j.epsl.2005.01.016

Mondal, P., Korenaga, J., 2018. A propagator matrix method for the Rayleigh-Taylor instability of multiple layers: A case study on crustal delamination in the early Earth. Geophysical Journal International 212, 1890–1901. https://doi.org/10.1093/gji/ggx513

Neil, E.A., Houseman, G.A., 1999. Rayleigh-Taylor instability of the upper mantle and its role in intraplate orogeny. Geophysical Journal International 138, 89–107. https://doi.org/10.1046/j.1365-246X.1999.00841.x

Sharp, D.H., 1984. An overview of Rayleigh-Taylor instability. Physica D 12, 3–18.

Taylor, G., 1950. The Instability of Liquid Surfaces when Accelerated in a Direction Perpendicular to their Planes. II. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 202, 81–96. https://doi.org/10.1098/rspa.1950.0086

Zhu, G., Gerya, T., Yuen, D.A., Honda, S., Yoshida, T., Connolly, J.A.D., 2009. Three-dimensional dynamics of hydrous thermal-chemical plumes in oceanic subduction zones. Geochemistry, Geophysics, Geosystems 10, 1–20. https://doi.org/10.1029/2009GC002625