
As a result of Earth’s mantle convection, rocks in the earth’s interior flow and develop a crystallographic texture. These textures reveal the planet’s thermal and tectonic history and are responsible for the viscous anisotropy, which can be used to study the planet’s deeper recesses that are not visible through other means. This necessitates the use of models that can predict the fabric generated on the basis of physical experiments. In this blog post, I will be giving a brief introduction to D-Rex, a crystallographic preferred orientation simulation code that is commonly used in the community.
What is CPO, and how does it offer insights into deformation in Earth’s mantle?
When a material is deformed, or in simpler words, squished, it either breaks or flows depending on its internal properties and surrounding environment. As a result, when rocks and minerals are deformed in the hot, high-pressure environment of the Earth’s mantle, they tend to flow. While many complex processes occur as the minerals are gradually squished, it results in the the rock mass obtaining a preferred orientation that records the deformation event (Carter and Ave’Lallemant, 1970). While the scale of these processes is on the order of micrometres (typical grain sizes in the mantle), this Crystallographic Preferred Orientation, or CPO, has an impact on mantle dynamics that occur over hundreds to thousands of kilometres. Because direct analysis of mantle deformation is not possible, a lot of effort was put into developing models that can predict the expected CPO given a set of imposed conditions and its evolution. In the geodynamics community, D-Rex (Kaminski et al, 2004) is the most widely used of the many models available to simulate CPO evolution.
What is D-REX, how does it simulate CPO ?

Srivatsan is a Ph.D. candidate at the Ben Gurion University of the Negev in Israel. His current research focuses on the influence of the microstructural evolution of olivine on upper mantle dynamics .
D-Rex is a kinematic mean-field model that accounts for both plastic strain and dynamic recrystallization. The model is considered to be kinematic as the stresses are represented as a velocity field, and mean-field in the sense that each grain is treated as an inclusion within a homogeneous body whose material properties are the weighted average of all the grains in the system. The ability of the algorithm to predict CPO evolution with reasonable accuracy at low computational cost while accounting for both plastic deformation and dynamic recrystallization distinguishes D-Rex from other models.
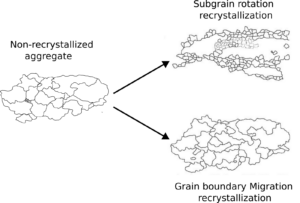
Figure 1: When a grain accumulates enough strain (left) , it undergoes recrystallization to form strain free grains either by subgrain rotation recrystallization (top right) or grain boundary migration recrystallization (bottom right). Modified from Stipp et al. (2002)
Given that dynamic recrystallization is an important feature of D-Rex, a quick review of some key concepts is in order. When grains are deformed, they accumulate strain and their internal strain energy increases. Recrystallization is a process that reduces internal strain energy by forming new strain-free grains (Urai et al, 1986). Recrystallization can occur in one of two ways. The first is subgrain rotation, which occurs when highly strained grains break up into smaller strain-free grains as a result of dislocation (linear crystalline defects) reorganisation into smaller substructures. The other is by grain boundary migration where highly strained grains are consumed by less strained grains due to differences in dislocation densities between neighbouring grains.
The model starts with n randomly oriented grains, their orientations defined by three euler angles, φ, θ, and ϕ. The grains have no dimensions, and their volume fraction, which is initially set to 1/n, determines their size. In the presence of an external velocity field, the system is then deformed. The grains begin to accumulate strain via dislocation creep or grain boundary sliding (GBS) depending on the volume fraction of the grain. The threshold separating dislocation and diffusion creep is defined as a fraction of the initial volume fraction.
How does olivine’s unique behavior challenge traditional models of mineral deformation?
An important assumption is that the mineral in question violates Von Mises’ criterion, which states that the mineral must have more than five independent slip systems for strain to be arbitrarily distributed between them. Olivine defies this rule by only having four independent slip systems. This means that only one slip system is active during a deformation event. While slip system activities are a large field of study in their own right, they are sensitive to temperature, water content, stress, and other factors. We can change which slip system is active in the model by varying the critical resolved shear stress (the minimum strain required for a slip plane to begin yielding) for each slip system in accordance with the conditions we want to model.
In D-Rex, recrystallization is controlled by two dimensionless input parameters λ* and M*. λ* refers to the nucleation efficiency, which essentially means the ability to “nucleate” new strain free grains. This value determines how much of the internal strain energy for the grain is recovered or reduced by subgrain rotation. Higher the value of λ*, lower is the amount of strain energy that is recovered by subgrain rotation. The remainder of the internal energy is recovered by grain boundary migration (GBM). The amount the grain changes its volume fraction depends on the value of M* and the difference between the internal strain energy of the grains and the mean strain energy of all n grains.
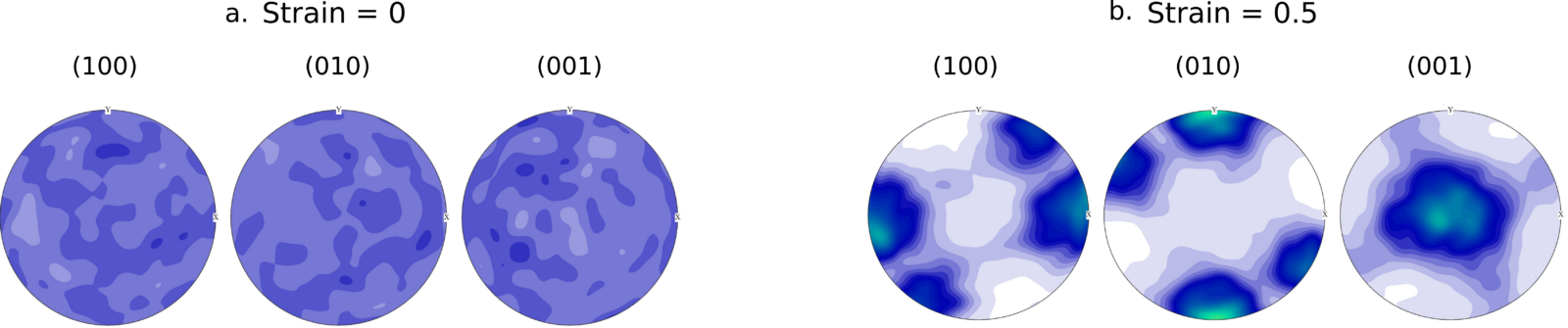
Figure 2: The CPO predicted by D-Rex at strains of a. 0 and b. 0.5, using values of λ* = 5 and M* = 125, recreating the results obtained in Kaminski et al (2004)
So in practice, the grains present in the aggregate are treated one of two ways by the algorithm. If the grain is bigger than the threshold, the grain will deform in the dislocation creep regime. In this regime, the crystallographic axes rotate, aligning the grain with the flow direction. The dislocation density increases and the strain energy increases. This implies that the grains in this group will shrink. The grains that deform in the GBS regime, the crystallographic axes are frozen and do not rotate. The dislocation density and strain energy is set to zero. This implies that the grains will start growing. It is also possible for grains to move between the two regimes over the course of the simulation.
To summarise, with a growing emphasis on studying anisotropy in the deep earth, the need to develop and apply better models of CPO estimation is critical. This post attempts to provide an introduction to one of the more commonly used packages, D-Rex. Despite its ability to accurately predict the fabric of a deforming aggregate, there is still work to be done to provide more insight into the influence of microstructural processes on the dynamics of the earth mantle.
Carter,N.L. & Ave'Lallemant H.G .(1970). High temperature flow of dunite and peridotite. Geological Society of America Bulletin , 81 (8).2181-2202. Kaminski , E., Ribe , N.M , Browaeys, J.T. (2004).D-Rex, a program for calculation of seismic anisotropy due to crystal lattice preferred orientation in the convective upper mantle. Geophysical Journal International, 158(2).744–752. Urai, J.L., Means, J.D., Lister, G.S. (1986). Dynamic Recrystallization of Minerals. Geophysical Monograph Series , 36.




