Geodynamics 101 – Viscous anisotropy

We are living in an anisotropic world. From rock-building crystals, ice, and trees growing in your garden to your favourite slice of cake many materials or objects has some anisotropic behaviour. What does this mean? Anisotropy (non-isotropy) implies that a material property depends on the direction of the measurement.

In geodynamics we often talk about seismic anisotropy, originating from microscopic or macroscopic layering, or crystallographic preferred orientation (CPO). Now here is the surprise: the same sources can create viscous anisotropy as well! So, in this blog post, let’s talk about the less famous of the two, the viscous anisotropy.

Anisotropic viscosity (AV) means that the material has different resistances to deformation depending on the direction of the stress applied to it.  Similarly to seismic anisotropy, viscous anisotropy can originate from extrinsic (e.g. layering) and intrinsic (e.g. crystallographic structure) anisotropy. In geodynamics, both kinds have their importance. Extrinsic viscous anisotropy can be relevant in the crust and the lithospheric mantle where rocks with different rheology are layered, or where the melt is forming (e.g. Lev and Hager, 2008; Perry-Houts and Karlstrom, 2019; de Montserrat et al., 2021). Intrinsic anisotropy originates from the crystallographic structures of rock-forming minerals. Indeed, most crystals are somewhat anisotropic. Some of the most studied examples are ice, calcite, and olivine (Martín et al., 2009; Hansen et al., 2012; Sly et al., 2020). As the main rock-forming mineral in the upper mantle is olivine, the following let’s focus on the anisotropic behaviour of this mineral.

Olivine has an orthorhombic crystalline structure. Some deformation mechanisms, especially dislocation creep, are highly sensitive to this structure. When deformation is achieved in an olivine grain by the propagation of linear defects (i.e. by dislocation creep) three slip systems can be used to achieve deformation. Of these three slip systems, two are very easy to activate while the third one is 1-2 orders of magnitude harder (Durham and Goetze, 1977). On large scale, this direction dependency is relevant when many olivine grains are aligned with each other (Hansen et al., 2016). We call this CPO – crystallographic preferred orientation. CPO develops when rocks undergo deformation, rotating each grain to align with the principal direction of deformation. It is important to note, that CPO, and therefore also seismic anisotropy are dependent on the history of strain (i.e. deformation) on the sample and not the velocity field. Hence, interpreting seismic anisotropy as the mantle flow direction is not always correct.

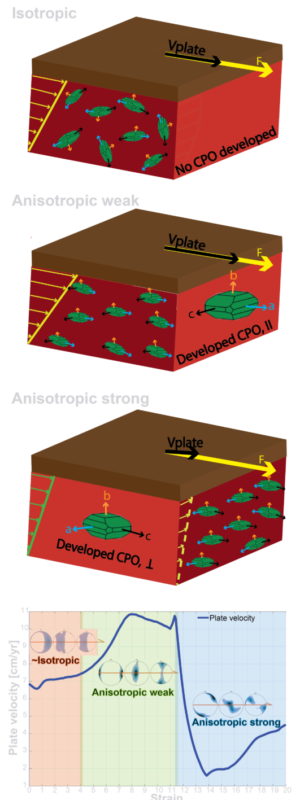
Simple model demonstrating anisotropic viscosity in the asthenosphere (source: Kiraly et al., 2020; anima-nfr.com)

CPO evolution depends on deformation history, and the deformation is dependent on the rheology, while the (anisotropic) rheology is dependent on the CPO, thus, there is a feedback effect between CPO and anisotropic viscosity. We can demonstrate this with a simple model. Let’s imagine that we have a rigid plate on the top of the anisotropic asthenosphere made out of olivine grains. We pull this plate with constant force (Figure 1). The asthenosphere initially has olivine grains that are randomly oriented with a uniform distribution (representing isotropy). As the asthenosphere deforms it becomes weaker as CPO develops parallel to the deformation and the plate’s movement on top. However, if we then pull the force perpendicular to the CPO (i.e. perpendicular to the weak direction of the olivine crystals), the asthenosphere will become anisotropically strong, reducing dramatically the plate velocity (Figure 1). Because of the increased viscosity, we will have reduced strain rates, and hence reduced amount of deformation. This results in a slow change in the CPO, which also means that the reduced plate velocity can last for a long time (Király et al., 2020).

The example above shows that anisotropic viscosity related to a strong CPO can significantly affect strain rates in the mantle. Now the question is, how, when, and where does anisotropic viscosity have a significant role on geodynamic processes. To address this question, one has to model together the development of anisotropic fabric and its effect on rheology. Modelling anisotropic viscosity related to olivine CPO involves i) the development of the texture due to deformation, which is parametrized based on laboratory experiments, ii) the calculation of the viscosity tensor based on the local CPO and the predicted stress or strain rate, and iii) using the full viscosity tensor (instead of a scalar viscosity) when solving the conservation equations. This can be computationally challenging.

One way to decrease computational costs is to assume that anisotropy has only 2 components; a shear and a normal viscosity, and use unit vectors – called directors – to represent the easy slip directions (Muhlhaus et al., 2003). In this case, the directors move and rotate with the velocity field in the model, and their orientation affects the viscosity. Using this method, Lev and Hager (2008, 2011) showed that anisotropic viscosity within the lithosphere can affect the grow-rate and the wavelength of lithospheric instabilities, while in a subduction zone, AV can channelize mantle flow in the mantle wedge, resulting also in an increased temperature above the slab.

Computational costs can also be reduced by investigating the role of AV in instantaneous models. For example, Liu et al., (2022), and (Mameri et al., 2021) both studied AV in lithospheric transform faults, finding that pre-existing textures can help focus deformation near previous faults and hence enhance the probability of their reactivation.

In Oslo, we are working on a project called ANIMA – Anisotropic viscosity in mantle dynamics, where our aim is to fully model the olivine CPO development and its viscous response feeding back to the solution and evaluate the role of AV for example in a subduction zone. We previously learnt that AV can affect the temperature above the slab. This might affect volcanism. A preliminary study by Wang et al. (in prep.) has found that CPO that develops in a subduction zone can be significantly modified when AV is considered.  Hence, we think the AV can not only affect the temperature field around slabs but also the mantle flow pattern, which in turn can have a role in subduction dynamics and geometry, as well as on the anisotropy pattern that we can expect to observe around subduction zones.

As a closing remark, we can conclude that anisotropic viscosity is present in many layers of Earth, and can be relevant from micro to macro scale processes. However, to fully understand when is this phenomenon really significant, we need some more work. Luckily, there is an increase in interest in this topic, with multiple research groups in tectonics and geodynamics aiming to tackle different aspects of AV.

References

Durham, W.B., and Goetze, C., 1977, Plastic flow of oriented single crystals of Olivine 1. Mechanical Data: Journal of Geophysical Research, v. 82, p. 5737–5753.

Hansen, L.N., Conrad, C.P., Boneh, Y., Skemer, P., Warren, J.M., and Kohlstedt, D.L., 2016, Viscous anisotropy of textured olivine aggregates: 2. Micromechanical model: Journal of Geophysical Research: Solid Earth, v. 121, p. 7137–7160, doi:10.1002/2016JB013240.

Hansen, L.N., Zimmerman, M.E., and Kohlstedt, D.L., 2012, Laboratory measurements of the viscous anisotropy of olivine aggregates: Nature, v. 492, p. 415–418, doi:10.1038/nature11671.

Király, Á., Conrad, C.P., and Hansen, L.N., 2020, Evolving Viscous Anisotropy in the Upper Mantle and Its Geodynamic Implications: Geochemistry, Geophysics, Geosystems, v. 21, p. e2020GC009159, doi:10.1029/2020GC009159.

Lev, E., and Hager, B.H., 2011, Anisotropic viscosity changes subduction zone thermal structure: Geochemistry, Geophysics, Geosystems, v. 12, doi:10.1029/2010GC003382.

Lev, E., and Hager, B.H., 2008, Rayleigh-Taylor instabilities with anisotropic lithospheric viscosity: Geophysical Journal International, v. 173, p. 806–814, doi:10.1111/j.1365-246X.2008.03731.x.

Liu, D., Puel, S., Becker, T.W., and Moresi, L.N., 2022, Analytical and numerical modeling of viscous anisotropy: A toolset to constrain the role of mechanical anisotropy for regional tectonics and fault loading:, https://eartharxiv.org/repository/view/3461/ (accessed March 2023).

Mameri, L., Tommasi, A., Signorelli, J., and Hassani, R., 2021, Olivine-induced viscous anisotropy in fossil strike-slip mantle shear zones and associated strain localization in the crust: Geophysical Journal International, v. 224, p. 608–625, doi:10.1093/gji/ggaa400.

Martín, C., Gudmundsson, G.H., Pritchard, H.D., and Gagliardini, O., 2009, On the effects of anisotropic rheology on ice flow, internal structure, and the age-depth relationship at ice divides: Journal of Geophysical Research: Earth Surface, v. 114, doi:10.1029/2008JF001204.

de Montserrat, A., Faccenda, M., and Pennacchioni, G., 2021, Extrinsic Anisotropy of Two-Phase Newtonian Aggregates: Fabric Characterization and Parameterization: Journal of Geophysical Research: Solid Earth, v. 126, p. e2021JB022232, doi:10.1029/2021JB022232.

Mühlhaus, H.-B., Čada, M., and Moresi, L., 2003, Anisotropic Convection Model for the Earth’s Mantle, in Sloot, P.M.A., Abramson, D., Bogdanov, A.V., Gorbachev, Y.E., Dongarra, J.J., and Zomaya, A.Y. eds., Computational Science — ICCS 2003, Berlin, Heidelberg, Springer Berlin Heidelberg, v. 2659, p. 788–797, doi:10.1007/3-540-44863-2_77.

Perry-Houts, J., and Karlstrom, L., 2019, Anisotropic viscosity and time-evolving lithospheric instabilities due to aligned igneous intrusions: Geophysical Journal International, v. 216, p. 794–802, doi:10.1093/gji/ggy466.

Sly, M.K., Thind, A.S., Mishra, R., Flores, K.M., and Skemer, P., 2020, Low-temperature rheology of calcite: Geophysical Journal International, v. 221, p. 129–141, doi:10.1093/gji/ggz577.