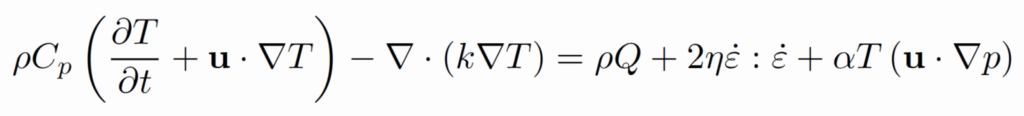
Earth’s structure and dynamics have evolved quite a lot since its formation, and so has mantle dynamics and convection patterns changed along with it. It turns out that phase transition in certain mantle minerals can be an important driver of this change. Today, Ranpeng Li from GEOMAR Helmholtz Centre for Ocean Research Kiel, Germany explains how coupling geodynamic models with thermodynamic principles can contribute towards a holistic understanding of the evolving mantle convection throughout the earth’s history.

Ranpeng is a PhD candidate at the GEOMAR Helmholtz Centre for Ocean Research Kiel. Her current project investigates how phase transitions shape mantle flow and convection styles. Her research interests also include advancing methods to couple thermodynamics with geodynamic models, as well as incorporating petrological and geochemical constraints into numerical simulations. She doesn’t like bugs – both inside and outside her code.
Earth’s mantle convects, cooling the planet and driving the tectonic plates that shape Earth’s surface. However, it is still an open question how the pattern of mantle convection has changed throughout Earth’s history. A key to answering this question may lie in the mineral assemblages in the mantle, which vary with depth due to changes in temperature and pressure. In this post, I introduce how transitions between different mineral phases can affect mantle flow and therefore the style of mantle convection. I also discuss our recent geodynamic study Li et al., 2025 [1], which suggests that mantle plumes could have been layered in Earth’s past due to a phase transition that occurs only in a hotter mantle.
Phase transition affect mantle flow
The dynamic effect of mineral phase transitions depends on their Clapeyron slope. The Clapeyron slope is the slope of the boundary between two mineral assemblages in pressure–temperature space. Endothermic transitions, which have a negative Clapeyron slope, occur at higher pressure when the temperature is lower. This can impede both downwelling and upwelling:
- A cold descending slab will cross the phase transition at a higher pressure (deeper depth) compared to the surrounding mantle. As a result, the slab will remain in the low-density phase while the surrounding mantle has already transitioned to a denser phase. This density difference produces a buoyancy force that hinders the slab from sinking.
- A hot rising plume transitions to a less dense phase at a lower pressure (shallower depth), making it denser than the surrounding mantle and subject to a negative buoyancy force, which hinders its ascent.
In today’s Earth, the ringwoodite ⇔ bridgmanite + ferropericlase transition at 660 km is the most important endothermic phase change. Together with the increase in viscosity between the upper and lower mantle, it is known to cause weak layering effects, such as impeding slabs (see Goes et al., 2017 [2], for a review). Phase transitions occur only within specific P–T ranges. When we examine the mantle’s phase diagram calculated by the thermodynamic software HeFESTo, as described in Stixrude and Lithgow-Bertelloni (2011) [3] (Figure 2), we see that the 660 transition does not extend into high temperatures. This means it may mainly affect descending slabs rather than plumes, and it may not significantly influence a hotter mantle, such as in Earth’s past.
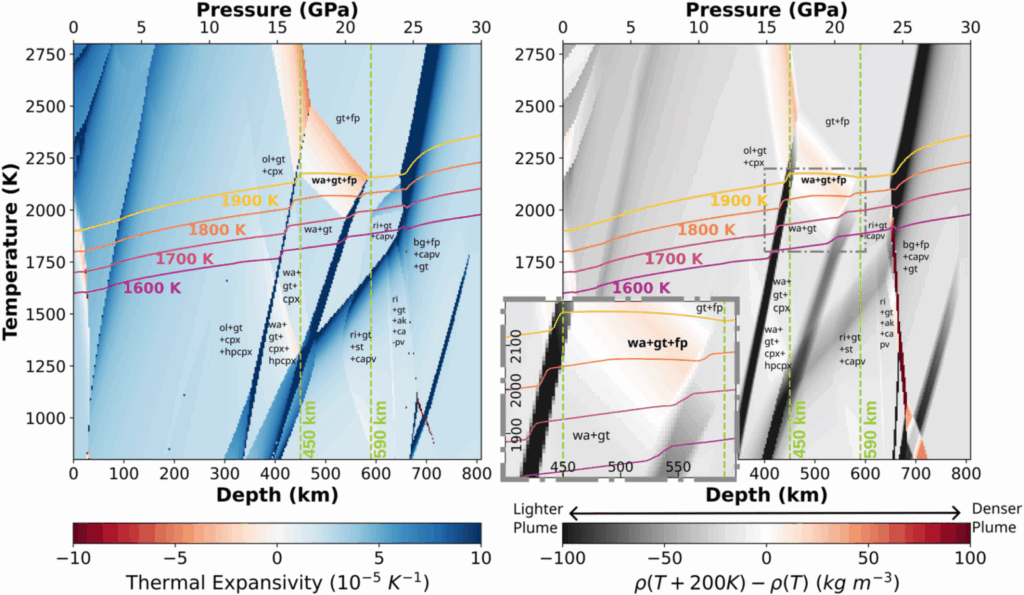
Figure 2: Material properties of pyrolite, a modeled bulk composition of Earth’s mantle, approximately 18% basalt and 82% harzburgite (Xu et al., 2008 [4]). Left: thermal expansivity plotted over pressure-temperature space; spikes indicate phase transitions. Some sharp transitions, like ringwoodite to bridgmanite + ferropericlase, appear only as small dots due to limited resolution. Right: density differences between two points at the same pressure but with a 200 K temperature difference, showing plume buoyancy relative to the mantle. Red areas mark endothermic phase transitions where plumes are denser and impeded. Solid colored lines show isentropes for various mantle potential temperatures. The inset highlights the wadsleyite ⇔ garnet (majorite) + ferropericlase transition region. This phase diagram is calculated by HeFESTo. For detailed mineral labeling, see Stixrude and Lithgow-Bertelloni (2011) [3], Figure 16.
However, when the mantle potential temperature is hotter than 1800 K (following the orange or yellow adiabat in Figure 2), the garnet (majorite) + ferropericlase assemblage (boxed by a dot-dashed line in the right panel) will occur and affect plumes. This suggests that, during Earth’s evolution, different phase transitions may have dominated the mantle at different cooling stages and induced different mantle convection patterns. Unlike the ringwoodite ⇔ bridgmanite + ferropericlase transition at 660 km, which is intensively studied, this wadsleyite phase transition has not been well explored. In the following section, I will introduce our recent work on modeling this effect with a new entropy method.
Modelling phase transitions with an entropy method
We approach this problem through numerical modeling with geodynamics code ASPECT [5], using an entropy method that captures the full effects of phase transitions (Dannberg et al., 2022 [6]). This method has two main advantages:
- Accurate phase relations: It uses a look-up table generated by thermodynamic software, which naturally incorporates complex phase relations through their physical property changes. Many studies simplify this with a “phase function” (manually defining a line and width where a phase transition occurs), which can oversimplify by assuming only one or two transitions and by assuming they extend across the full P-T range. By contrast, our method couples thermodynamics and geodynamics more realistically by using the calculated equation of state directly.
- Numerical stability while fully including latent heat: Although it is possible to use a look-up table in the traditional temperature-pressure formulation, solving the energy equation for entropy has numerical and thermodynamic advantages. When formulating energy equations in terms of temperature and pressure, material properties such as thermal expansivity and specific heat jump at a phase transition when latent heat is absorbed or released. These spikes in material properties create numerical instability when latent heat is included, especially for sharp phase transitions. The entropy formulation avoids this problem. As shown in the equation, thermal expansivity and specific heat do not appear. The entropy method therefore allows us to realistically model sharp phase transitions and their full dynamic effects on mantle processes.
Energy conservation for temperature:
Energy conservation for entropy: 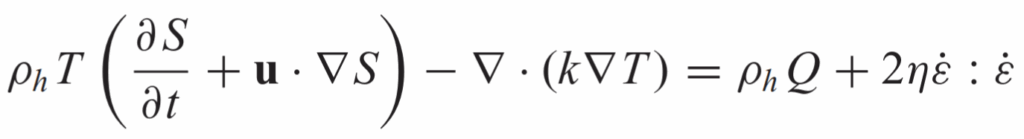
u is the velocity, p is the pressure, T is the temperature ρh is the density, g is the gravity vector, Cp is the specific heat capacity of the material, k is the thermal conductivity, ε̇ is the strain rate, Q is the intrinsic specific heat production,and α is the thermal expansion coefficient. To include latent heat, we consider α and Cp to be effective properties.
Importantly, we still have temperature values because they can be looked up from entropy-pressure tables, and the entropy-to-temperature conversion is unique. If you want to learn more about why we use entropy, you can find further details in Bob’s and Juliane’s post.
wadsleyite to garnet (majorite) + ferropericlase stalls plume in Earth’s past
In Figure 3, you can find snapshots of three different models. These models run forward in time, include plastic deformation to form plate-like subduction, but start with different core-mantle boundary temperatures and different mantle temperatures. The top panel starts with an isentropic value of 2535.08 J/kg/K, corresponding to a mantle potential temperature of 1600 K—similar to today’s Earth. The bottom panel starts with an isentropic value of 2687.748 J/kg/K (1800 K), representing the hotter mantle in the past. Petrological studies estimate mantle cooling rates by studying the composition of igneous rock. For example, Herzberg et al. (2010) [7] use non-arc basalt to infer a mantle cooling rate of up to ~100 K/Gyr. Therefore, this hotter model can represent Earth roughly 2 billion years ago.
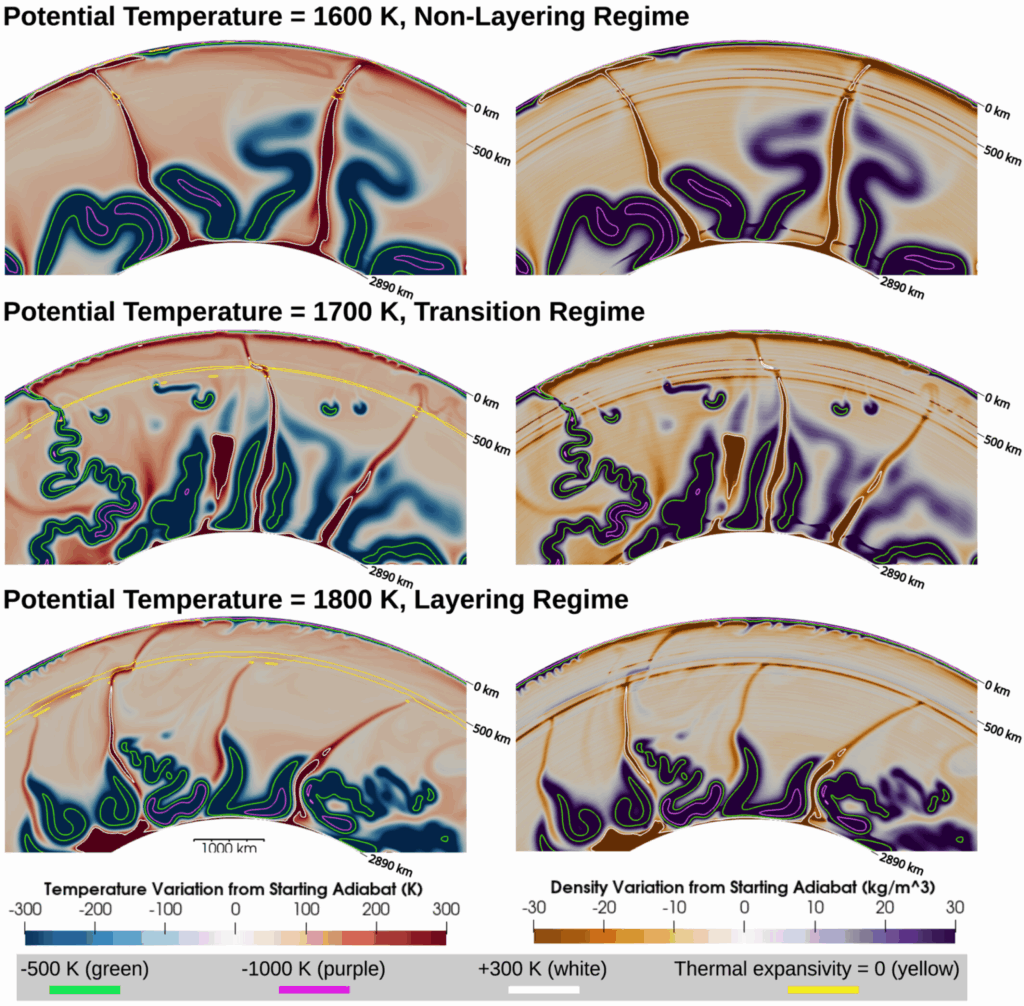
Figure 3: Snapshots of three models that have different dominated phase transitions, resulting in distinct convection styles. Yellow lines mark transitions from positive to negative effective thermal expansivity, showing the regions of phase transitions with negative Clapeyron slope. Click here to see videos of full model evolution: Top panel video, Middle panel video, Bottom panel video.
When we compare them, we see that in the 1800 K model, plumes are strongly impeded at transition zone depths. This is due to the wadsleyite ⇔ garnet (majorite) + ferropericlase phase transition discussed earlier. In models hot enough for this phase transition to occur, we observe a wide variety of stalled plume morphologies (see Figure 4).
The wadsleyite ⇔ garnet (majorite) + ferropericlase transition can trap hot material, leading to elevated temperatures at depths of 500-650 km in a mantle hotter than today’s. These results imply that mantle convection may have been partially layered early in Earth’s history. We quantify the degree of this layering effect and find that it can reduce a plume’s vertical mass transport between the lower and upper mantle by almost hundred percent. While it does not really impede slabs and therefore does not cause fully layered convection, the strong impedance of plumes may still influence Earth’s cooling path and how Earth’s deep interior is returned to the surface through mantle upwellings. In addition, many secondary plumes rise from this hot layer, which can also affect volcanism at the surface and plume-induced tectonic movement.
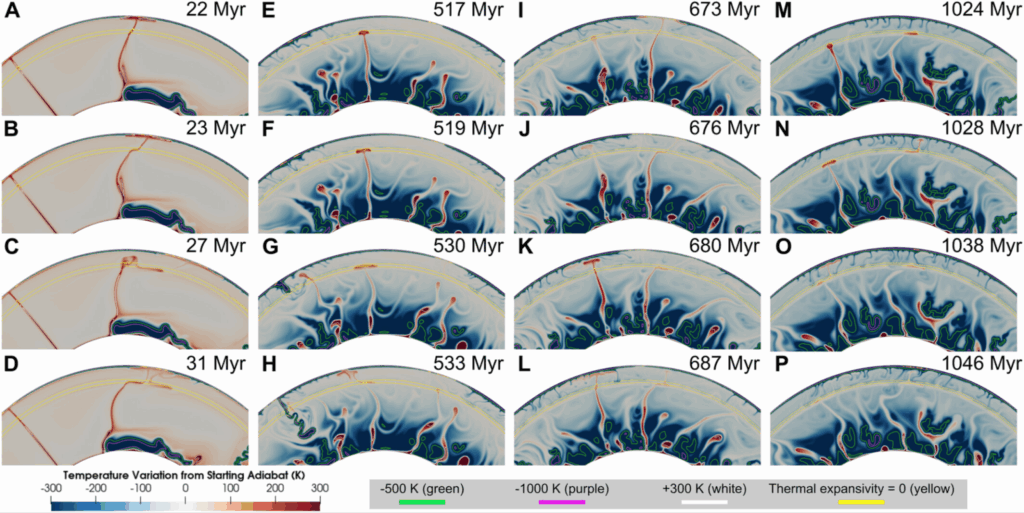
Figure 4: Plume morphology in a long-term model that gradually cools from 1900 K to today’s mantle temperature. Tilted plumes are more strongly impacted by the wa ⇔ gt + fp transition, causing them to stall. Their stagnant heads spread horizontally at ~500 km depth and later spawn one or more secondary plumes from this hot layer.
Conclusion
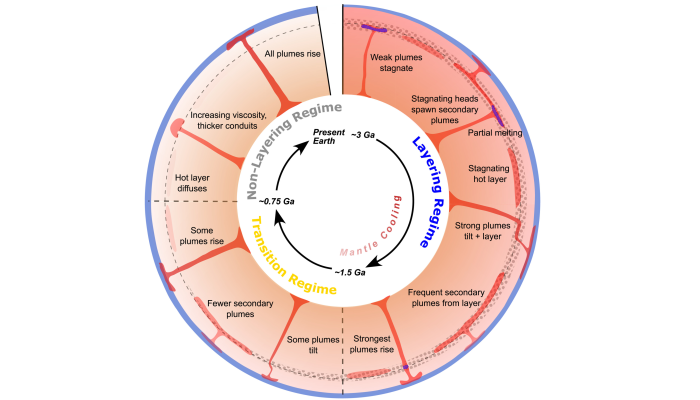
At the end, I would like to show a figure summarizing the possible stages Earth may have undergone (figure 1). The wadsleyite ⇔ garnet (majorite) + ferropericlase transition may have caused strong plume layering until Earth cooled below ~1750 K. This may have been followed by a transitional regime, during which the effect persisted but gradually weakened. Beyond Earth’s mantle in the past, this phase transition may still play a significant role on hotter planets—such as Venus, where more details can be found in Madeline’s post. Back on Earth, though the mantle today may be too cool for this phase transition to occur, its long-lasting influence on Earth’s history remains an interesting topic for further exploration (Li et al., 2025 [1]).
References: [1] Li, R., Dannberg, J., Gassmöller, R., Lithgow-Bertelloni, C., & Stixrude, L. (2025). How phase transitions impact changes in mantle convection style throughout Earth's history: From stalled plumes to surface dynamics. Geochemistry, Geophysics, Geosystems, 26, e2024GC011600. https://doi.org/10.1029/2024GC011600 [2] Goes, S., Agrusta, R., van Hunen, J., & Garel, F. (2017). Subduction-transition zone interaction: A review. Geosphere, 13(3), 644–664. https://doi.org/10.1130/ges01476.1 [3] Stixrude, L., & Lithgow-Bertelloni, C. (2011). Thermodynamics of mantle minerals-II. Phase equilibria. Geophysical Journal International, 184(3), 1180–1213. https://doi.org/10.1111/j.1365-246x.2010.04890.x [4] Xu, W., Lithgow-Bertelloni, C., Stixrude, L., & Ritsema, J. (2008). The effect of bulk composition and temperature on mantle seismic structure. Earth and Planetary Science Letters, 275(1–2), 70–79. https://doi.org/10.1016/j.epsl.2008.08.012 [5] Heister, T., Dannberg, J., Gassmöller, R., & Bangerth, W. (2017). High accuracy mantle convection simulation through modern numerical methods. II: Realistic models and problems. Geophysical Journal International, 210(2), 833–851. https://doi.org/10.1093/gji/ggx195 [6] Dannberg, J., Gassmöller, R., Li, R., Lithgow-Bertelloni, C., & Stixrude, L. (2022). An entropy method for geodynamic modelling of phase transitions: Capturing sharp and broad transitions in a multiphase assemblage. Geophysical Journal International, 231(3), 1833–1849. https://doi.org/10.1093/gji/ggac293 [7] Herzberg, C., Condie, K., & Korenaga, J. (2010). Thermal history of the Earth and its petrological expression. Earth and Planetary Science Letters, 292(1–2), 79–88. https://doi.org/10.1016/j.epsl.2010.01.022