
Assistant Professor Juliane Dannberg, University of Florida.
In January of this year, Bob Myhill wrote about the coupling of geodynamics and thermodynamics, and why this coupling is so valuable. This blog post, Juliane Dannberg follows up on this topic, looking at it from the geodynamics perspective. In other words, discussing the question: Where does it make a difference in geodynamic models if we include realistic thermodynamic models or not?
In geodynamics, our equations are usually formulated in terms of temperature and pressure (rather than entropy and density). This is how they can be written (assuming that we do not take into account inertia):
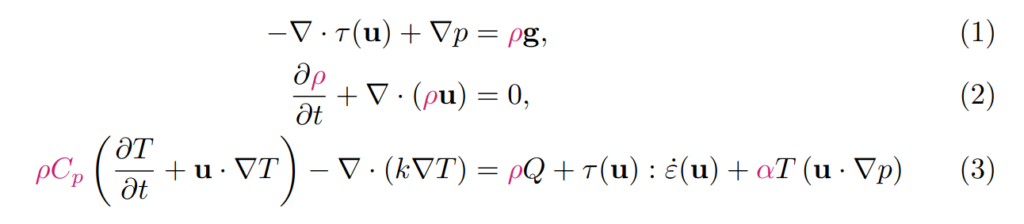
τ is the deviatoric stress, u is the velocity, p is pressure, ρ is density, g is gravitational acceleration, t is time, Cp is the specific heat capacity, T is temperature, k is thermal conductivity, Q is the radiogenic heat production rate, ε is the deviatoric strain rate, and α is the thermal expansivity.
Since thermodynamics allows us to compute the stable mineral assemblage under given conditions, it provides a way of computing material properties such as density, thermal expansivity, heat capacity and compressibility in the mantle. These material properties are highlighted in the equations above, and they can be taken from a thermodynamic dataset. As Bob Myhill explained in his post, there are several thermodynamic programs (such as PerpleX, ENKI and BurnMan) that can process these datasets and output material properties as a function of entropy and density (or temperature and pressure, as would be required by the equations above). This is often done in the form of a look-up table for a specific chemical composition. A simpler alternative that many geodynamic models use is to assume that some of these properties are constant or can be parameterized. For example, many codes rely on a reference profile for the density, and/or assume that properties such as the thermal expansivity or specific heat are constant. Such approximations are appropriate for many applications, but below I will discuss key differences between models with simplified material properties, and models that instead rely on a thermodynamic dataset.
Pressure and temperature-dependence of material properties
It is obvious that the density is a key property for mantle dynamics, since it determines the buoyancy forces within a model. Consequently, geodynamic models usually consider temperature- and composition-dependent density as well as density changes at major phase transitions, depending on the application. However, properties like thermal expansivity, heat capacity and compressibility are often assumed to be constant (or zero, for the compressibility in incompressible models). This is done despite several studies having shown that using a pressure- and temperature dependent thermal expansivity causes a major change in the convection style. For example, hot plumes become stronger, and the descent of cold downwellings is inhibited (Schmeling et al., 2002, Tosi et al., 2013). In particular the temperature-dependence of thermal expansion is so strong that models including only the effects of depth-dependence may underestimate surface heat flow and plate velocities by as much as 20% and 50% (Ghias and Jarvis, 2008). Compressibility is similarly important, leading to a volume decrease of approximately 50% from the surface to the core-mantle boundary. Cold downwellings contract and hot upwellings expand while moving through the mantle.
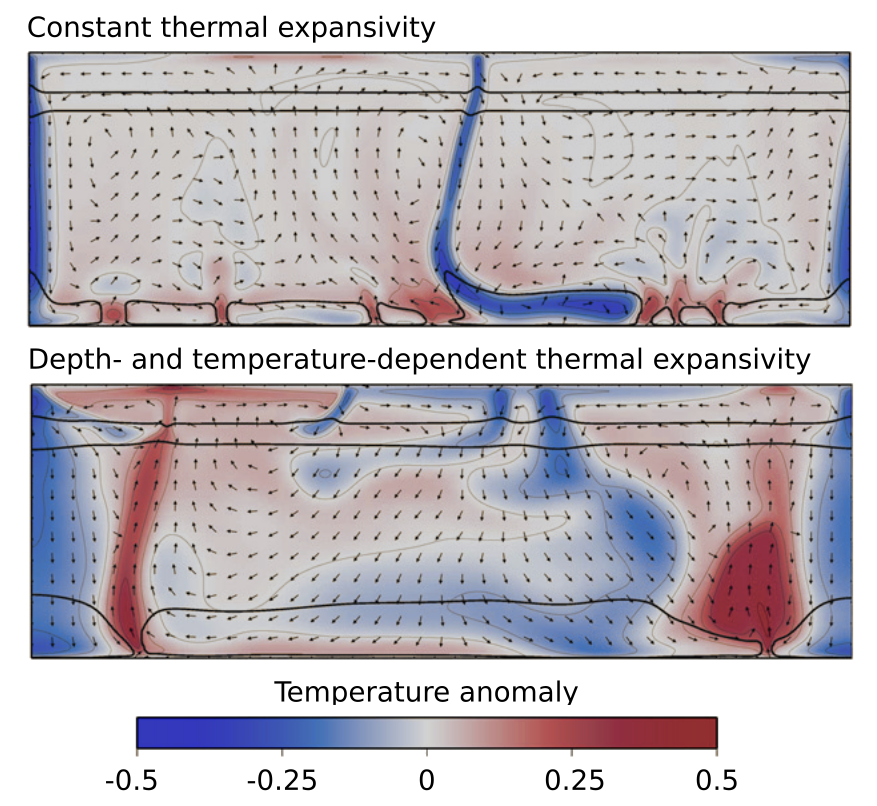
Convection model from Tosi et al., 2013, featuring a model with constant thermal expansivity (top) and pressure- and temperature-dependent thermal expansivity (bottom). Cold downwellings are inhibited, and plumes are stronger in the bottom panel. (Image modified from Tosi et al., 2013, https://doi.org/10.1016/j.pepi.2013.02.004)
These types of effects, at least in terms of the pressure-dependence, are relatively simple to include in geodynamic models. They can often be approximated by parameterizing the material properties, for example as a function of depth, or as a function of both depth/pressure and temperature. At least in global convection simulations, these parameterizations yield similar thermal and thermochemical structures as simulations that use free energy minimization to compute mineral assemblages and the resulting thermodynamic properties (Nakagawa et al., 2009). However, there are a number of applications where these simple parameterizations or the introduction of a depth-dependent reference profile are not enough to capture dynamic effects. Below, I will illustrate these effects using three different examples.
Case 1: Dynamic effects of compressibility: thermal expansion and contraction in boundary layers
When models use a reference profile for density in the mass conservation equation, the volume of material can only change if it moves up or down. This accurately reflects volume changes along a mantle adiabat, but does not include expansion or contraction due to conductive heating or cooling. Take the example of newly generated oceanic lithosphere at a mid-ocean ridge: Over time, as the plate cools down, it becomes denser and contracts. This contraction can build up stresses in the plate, and contribute to deformation at faults. The image below shows a simplified example of this problem: What happens at the interface between old (cold) crust, and recently formed crust that is hot and rapidly cooling down? In this example, old and young crust are separated by a weak fault zone. As the hot crust in the hanging wall (left part of the model) cools, it becomes denser and contracts, leading to downward motion of the material at the surface. The old crust in the footwall (right part of the model) does not deform, since it has already cooled down. This difference in contraction causes deformation along the weak fault zone separating the old and young material, and causes a change in topography across the fault (in this example from Gassmöller et al, 2020, the model generates a topography of ∼229 m over 5 Myr). The corresponding deviatoric stresses can be seen in the top right panel. Models that use a reference profile do not predict this deformation or stress build-up, and do not develop topography across the fault (bottom right panel).
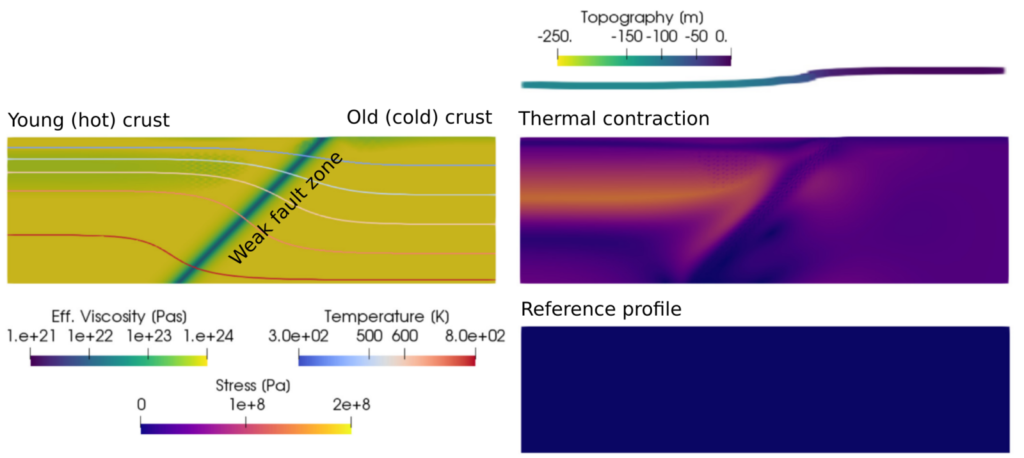
Crustal-scale model from Gassmöller et al, 2020, illustrating the effects of thermal contraction. The left panel shows the viscosity (background) and temperature (contours), the right panel shows the deviatoric stress.
Case 2: Volume change at phase transitions
Mineral phase transitions can have an important influence on mantle convection. Depending on their properties, they can accelerate or stall upwellings and downwellings on their way through the mantle, and even induce layered convection (e.g. Christensen & Yuen, 1985; Peltier & Solheim, 1992). They also might be important for why some slabs stagnate in the transition zone. Again, we have the choice of parameterizing phase transitions or getting their properties from a thermodynamic dataset. Many models parameterize major mantle phase transitions using the approach of a phase function that is 0 above and 1 below the transition, and represents the amount of material that has undergone the transition (Christensen & Yuen, 1985). This approach has the advantage that it is easy to implement, and allows it to vary individual parameters of each transition (such as its density jump or its Clapeyron slope) independently. However, it limits the number and complexity of phase transitions that can be implemented. For example, many mineral phase transitions in the mantle only exist in a narrow temperature–pressure range and their properties vary with temperature and pressure. On the other hand, taking the material properties from a thermodynamic dataset (e.g. Nakagawa et al., 2009) automatically includes all of the relevant mineral phase transitions and their complexity. If the density everywhere in the equations is taken from the thermodynamic model (rather than relying on a parameterization or a reference profile), geodynamic models can take into account the effect of phase transitions on both buoyancy and volume changes.
This means that phase transitions could have very different effects on slabs compared to plumes. For example, at low temperatures, such as in subducted slabs, the ringwoodite to bridgmanite + ferropericlase transition has a negative Clapeyron slope, inhibiting cold downwellings. But at high temperatures, such as in hot plumes, or earlier in Earth’s history, ringwoodite is no longer stable, and the transition to bridgmanite instead has a positive Clapeyron slope, accelerating the motion of hot material. The figure below shows the density difference of both plumes and slabs compared to the average mantle, highlighting the different effect of phase transitions on plumes and slabs.
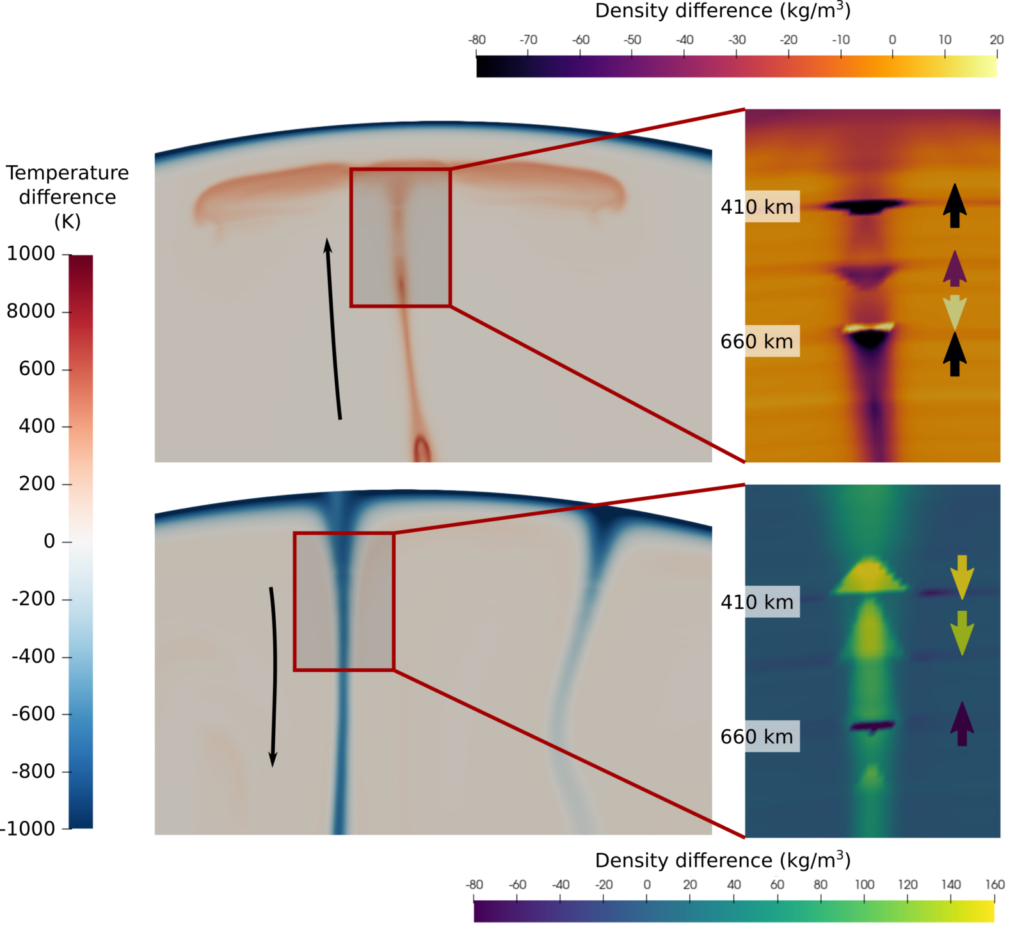
Snapshots of a simplified convection model (run by Ranpeng Li), using a thermodynamic dataset (Stixrude and Lithgow-Bertelloni, 2011, material properties computed with HeFesTo). Panels on the left show temperature, and panels on the right show the density difference between a hot upwelling (top) and a cold downwelling (bottom) and the background mantle. The buoyancy effect of phase transitions is indicated by the arrows: The phase transition interface is distorted by the hot and cold temperatures according to each transition’s Clapeyron slope, causing an accelerating effect for transitions with a positive Clapeyron slope (upwards force for plumes, downwards force for slabs) such as at 410 km depth, and a decelerating effect for transitions with a negative Clapeyron slope (downwards force for plumes, upwards force for slabs) such as at 660 km depth.
Case 3: Latent heat of phase transitions
While latent heat is commonly considered less important than the buoyancy effect of phase transitions due to the change of the transition depth with temperature, it still has several important effects. Latent heat release or consumption causes temperatures changes on the order of 100 K or less at major mantle phase transitions along a mantle adiabat. This means that, for example, the transition zone is hotter than it would be in a model that does not consider latent heat. This change in temperature due to latent heat can have an impact on the viscosity, on the speed of reactions (such as in a metastable olivine wedge), and it can further distort the phase transition interface. For example, during shallow low-angle subduction, latent heat effects can result in a substantial increase of the flat slab length by 300–400 km (van Hunen at al., 2001). But these effect are not only important for mantle dynamics, but also for the comparison of models to seismic observations.
When considering latent heat, we arrive at the problem that Bob Myhill pointed out in his post: The reactions associated with phase transitions can lead to very narrow spikes in material properties such as the thermal expansivity, specific heat and compressibility. To accurately model latent heat effects, these spikes have to be resolved in the geodynamic model. However, as Bob points out, if we solve our equations for temperature and pressure, material properties such as thermal expansivity and heat capacity are both discontinuous and may vary by orders of magnitude, or may even be infinite. This is not only a problem for accuracy, but may simply cause the solver to fail to converge to a solution. Bob showed that the way to avoid all discontinuities in material properties was to calculate properties as a function of entropy and density. But solving the conservation equations for these variables would require big changes to any geodynamic modeling software. As long as our geodynamic simulation involves only a single bulk composition, and our phase diagram does not contain any univariant points (or they are not important for the particular problem we want to model), we may also be able to get away with using pressure and entropy (instead of pressure and temperature). In this case, phase transitions that were univariant lines in pressure–temperature space now have a finite width (so that material properties are not infinite any more). In addition, we do not need to compute temperature changes associated with latent heat release or consumption at the transitions, because entropy stays constant along an adiabat.
This allows us to include very thin phase transitions in a geodynamic model without additional numerical challenges. One example is the ringwoodite to bridgmanite + ferropericlase reaction, which is thought to occur over less than a kilometer in depth. Modeling phase transitions with a realistic thickness is important to accurately reflect their effect on dynamics. Simulations show that the thinner a phase transition compared to the length scale of flow, the bigger its impact (e.g. Peltier & Solheim, 1992; Tackley, 1995). For example, in a model with just one phase transition with a negative Clapeyron slope, the thickness of the transition can be the deciding factor on the style of convection: one convection cell, episodic overturns, or layered convection.
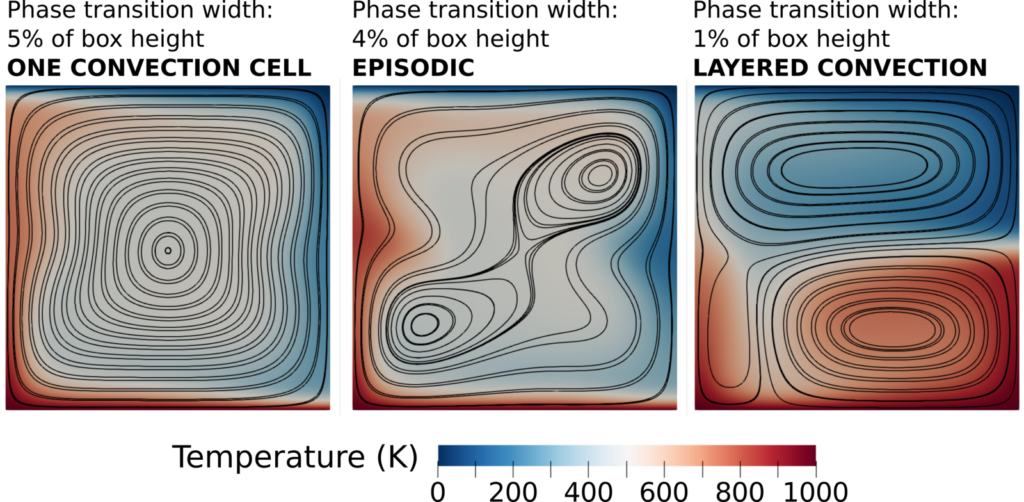
Model setup of Christensen & Yuen (1985). The three panels show three different models with the same setup with a phase transition with a negative Clapeyron slope at mid depth, except that the width of the phase transition decreases from the left to the right panel. This results in a change in convective regime.
With the examples above, I hope I have been able to convince you that it is important to make use of the information that thermodynamics can provide, and that it can make a substantial difference in the predictions of geodynamic models. A lot of progress is being made in coupling geodynamic and thermodynamic models, and I am looking forward to seeing more of these models in the future.
References: Christensen, U. R., & Yuen, D. A. (1985). Layered convection induced by phase transitions. Journal of Geophysical Research: Solid Earth, 90(B12), 10291-10300. Peltier, W. R., & Solheim, L. P. (1992). Mantle phase transitions and layered chaotic convection. Geophysical Research Letters, 19(3), 321-324. Tackley, P. J. (1995). On the penetration of an endothermic phase transition by upwellings and downwellings. Journal of Geophysical Research: Solid Earth, 100(B8), 15477-15488. van Hunen, J., van den Berg, A. P., & Vlaar, N. J. (2001). Latent heat effects of the major mantle phase transitions on low-angle subduction. Earth and Planetary Science Letters, 190(3-4), 125-135. Schmeling, H., Marquart, G., & Ruedas, T. (2003). Pressure-and temperature-dependent thermal expansivity and the effect on mantle convection and surface observables. Geophysical Journal International, 154(1), 224-229. Stixrude, L., & Lithgow-Bertelloni, C. (2011). Thermodynamics of mantle minerals-II. Phase equilibria. Geophysical Journal International, 184(3), 1180-1213. Ghias, S. R., & Jarvis, G. T. (2008). Mantle convection models with temperature‐and depth‐dependent thermal expansivity. Journal of Geophysical Research: Solid Earth, 113(B8). Nakagawa, T., Tackley, P. J., Deschamps, F., & Connolly, J. A. (2009). Incorporating self‐consistently calculated mineral physics into thermochemical mantle convection simulations in a 3‐D spherical shell and its influence on seismic anomalies in Earth's mantle. Geochemistry, Geophysics, Geosystems, 10(3). Tosi, N., Yuen, D. A., de Koker, N., & Wentzcovitch, R. M. (2013). Mantle dynamics with pressure-and temperature-dependent thermal expansivity and conductivity. Physics of the Earth and Planetary Interiors, 217, 48-58. Gassmöller, R., Dannberg, J., Bangerth, W., Heister, T., & Myhill, R. (2020). On formulations of compressible mantle convection. Geophysical Journal International, 221(2), 1264-1280.
