The Geodynamics 101 series serves to showcase the diversity of research topics and methods in the geodynamics community in an understandable manner. We welcome all researchers – PhD students to Professors – to introduce their area of expertise in a lighthearted, entertaining manner and touch upon some of the outstanding questions and problems related to their fields. This month Vojtěch Patočka from the Charles University in Prague, Czech Republic, discusses the rheology of the lithosphere and its food analogies. Do you want to talk about your research? Contact us!
It is becoming increasingly obvious that geodynamics and cooking are closely related, especially to the participants of a recent workshop in the Netherlands. Food analogies are helping students to get a physical grasp of continuum mechanics and to forget their lunches at university canteens. Here we take a basic look at a field where talking about fine cuisine has long been established: the rheology of the lithosphere. But first we step back a little.
Elastic solids deform when a force is applied and return to their original shape when the force is removed. Viscous fluids eventually take the shape of a container that is applied to them: they spontaneously flow to a state of zero shear stress. One can hardly imagine more different materials than these two, and yet the Earth’s mantle is sometimes modelled as an elastic shell and sometimes considered to be a viscous fluid.
You may be thinking:
Sure, it is a matter of what time scale is relevant for the process at hand
– just as J.C. Maxwell already thought: “Hence, a block of pitch may be so hard that you cannot make a dent in it by striking it with your knuckles; and yet it will in the course of time flatten itself by its weight, and glide downhill like a stream of water.” To visualise Maxwell’s dreams, the University of Queensland has been continuously running a pitch drop experiment for the past 90 years.
It is for the reason above that seismologists vibrate a Hookean Earth in their computers and geodynamicists play with viscous fluids. Are both of them right? Surprisingly, only the seismologists are. There is direct evidence that the outer parts of planetary mantles have an important elastic component even on geological time scales, which implies that treating the entire mantle as viscous is wrong. A textbook example can be found near the deepest part of the world’s oceans. Fig. 1, adopted from the bible by Turcotte & Schubert, shows how one can fit the bathymetric profile across the Mariana trench to the shape of a bent elastic plate. Note that the slab is subducting at the rate of a few centimeters per year, meaning that each segment of the slab is loaded for tens of millions of years before it disappears into the mantle and it still retains the elastic strain.
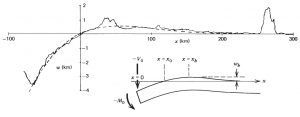
Figure 1: Comparison of a bathymetric profile across the Mariana trench (solid line) with the deflection of a thin elastic plate subject to end loading (dashed line). Distance xb–x0 is the half-width of the forebulge from which the thickness of the plate can be inferred. Adopted from section 3 of Turcotte & Schubert, 2002.
Flexure studies and effective elastic thickness
Other similar examples, referred to as flexure studies, are summarised nicely by Watts et al., 2013. They include deflections under seamounts that litter oceanic floors and also some much longer lasting structures, such as continental foreland basins with the Ganges basin representing a particularly popular case. The free parameter that plays first fiddle in flexure studies is the thickness of elastic plate that matches observation. What does the resulting value, known as the effective elastic thickness, actually tell us?
I will use a dirty trick of bad journalism and quote an innocent geology blog slightly out of context:
The Indian crust is cold and rigid. Clever folk can do the maths on the shape of the crust as it bends down. This confirms that the pattern matches the model for rigid, elastic deformation. It also allows us to calculate the plate’s flexural rigidity, which is a measure of its strength. This means quantifying the rheology of real bits of the earth, which is a very useful trick
The math referred to involves purely elastic deformation and the flexural rigidity in its definition depends only on Young’s modulus, thickness, and Poisson ratio of the plate. Are the clever folk trying to fool us into believing that the lithosphere is an elastic plate? From lab measurements and geology we know for sure that it is not. Brittle failures are an abundant feature in both the crust and upper mantle, and various solid state creep mechanisms must be active in the deeper parts of the lithosphere.
The best fit for the Indo-Australian plate subducted below the Ganges basin is obtained with an elastic plate of circa 90 km thickness and for the Pacific plate at the Mariana trench it is circa 30 km. In both cases the plates are actually much thicker. What the computed values of 90 and 30 km tell us, is how much of elastic energy is present within the plate over the process of subduction, despite the brittle failures and despite the ductile creep activated in response to shear stresses within the plate.
To move away from sinking slabs, think about the story of a seamount that popped out on an ocean floor. Imagine a fresh, unstressed segment of oceanic plate that gets suddenly loaded by the uninvited underwater volcano. Small intra-plate fractures may immediately form, depending on the size of the load, and ductile creep will begin to continuously deform the plate’s deeper parts. The elastic energy present in the material upon loading gets partially released, either immediately through cracking or gradually via ductile creep. Measuring effective (or equivalent) elastic thickness merely tells us the amount of elastic energy left at the time of measurement.
This is all well known to the authors of flexure studies. In fact, they often re-draw the Christmas trees (see Fig. 2) and provide constraints on rheological zonation of the Earth. Pioneers in the field are E.B. Burov and A.B. Watts, whose papers are often accidentaly googled by chefs searching for latest trends in the dessert industry due to the extensive use of the words jelly sandwich and crème brûlée ([4] and [5], for breakfast see also [6]). The main point of the discussion is to determine the brittle/ductile transition and the active creep mechanism in a realistic, compositionally stratified lithosphere. This is usually complicated by the fact that lithologies measured in lab experiments strongly depend on composition, water content and temperature – and these are not well constrained in the real Earth.
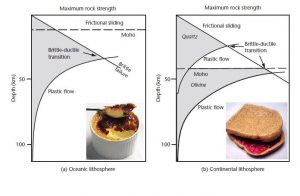
Figure 2: The total force per unit width necessary to break or viscously deform a lithospheric section at a given strain rate. Plots like these are known as the Christmas tree plots, here adopted from Basin Analysis by P.A. Allen and J.R. Allen (without the food).
A geodynamical paradox
It is a paradox that in geodynamical modeling we often use the constraints from flexure studies and at the same time forget about elasticity, without which there would be no such studies at all. Recall that the primary result of shape fitting, for instance of the one depicted in Fig. 1, is that some elastic support is present. As I warned above, one can only hardly distinguish between a purely elastic plate of a given thickness and some other, thicker elasto-brittle or visco-elastic plate when looking at its surface flexure. However, there must be elasticity involved in some form: purely viscous or visco-plastic plates would not form the observed forebulge. Forebulges are related to the way elastic rods and plates transfer bending moment throughout the medium.
The tendency to disregard elasticity may be related to the way we use the word ‘rigid’ in the context of plate tectonics. In physics, rigid means ‘not deforming’. For plate tectonics to work the plates do not have to be rigid. They may not flow apart on geological time scales (they must remain plates), but some relatively small reversible deformation is well compliant with the concept. So the main point is: Be the lithosphere a sandwich or a crème brûlée, it is also flexible, even on geological time scales.
Batman and gummy bears
If you are in numerical modelling then there is good news for you. In the past two decades, several Robins, including myself, have enhanced the Batman codes to account for elasticity. Maybe all you have to do is to switch on the right button. The implementation of visco-elasticity is usually based on a method developed by L. Moresi, who also, according to a previous Geodynamics 101 blog post, coined the hero terminology I just borrowed. Visco-elasticity works in quite a simple way, just like gummy bears. I am currently running an experiment with them. They quickly bend and squeeze when tortured, their resistance governed by their shear modulus, and recover when let go. At the same time they can flow, the resistance being controlled by their viscosity. Let’s put a book on top of one and see if we can find its nose after a week…
The elasticity button
Don’t be afraid to push the elasticity button, if your code has it. Usually it won’t do anything dramatic to your simulations, but exceptions exist [7]. In thermal convection models without plate tectonics there is not much feedback between the lid and the underlying mantle, and so only the build-up of dynamic topography is affected [8]. In subduction modeling your slabs may obtain different dipping angles. In continental extensions the total amount of extension will become more important than the divergence rate [9]. And in the simulation of continental shortening mentioned above [7], the elastic energy accumulated in the entire model gets partially released upon the onset of a shear zone. In such cases, i.e. when large scale elastic strains suddenly influence a much smaller region, one can expect some earthquakes to shake the conventional view of elasticity in geodynamical modeling. And if you still do not care about elasticity but yet you made it all the way here, then you deserve a bonus: the convergence of Stokes solvers is way better for visco-elastic rheologies than for the viscous ones – if you are numerically troubled by large viscosity contrasts of your model, elasticity is the way to go for you.
References (1) D.L. Turcotte and G. Schubert (2002), Geodynamics (2) A.B. Watts, S.J. Zhong, and J. Hunter (2013), The Behavior of the Lithosphere on Seismic to Geologic Timescales, doi: 10.1146/annurev-earth-042711-105457 (3) P.A. Allen and J.R. Allen (2005), Basin analysis : principles and applications (4) E.B. Burov and A.B. Watts (2006), The long-term strength of continental lithosphere: 'jelly sandwich' or 'creme brulée'?, doi: 10.1130/1052-5173(2006)016 (5) E.B. Burov (2009), Time to burn out creme brulee?, doi: 10.1016/j.tecto.2009.06.013 (6) E.H. Hartz, Y.Y. Podladchikov (2008), Toasting the jelly sandwich: The effect of shear heating on lithospheric geotherms and strength, doi: 10.1130/G24424A.1 (7) Y. Jaquet, T. Duretz, and S.M. Schmalholz (2016), Dramatic effect of elasticity on thermal softening and strain localization during lithospheric shortening, doi: 10.1093/gji/ggv464 (8) V. Patocka, O. Cadek, P.J. Tackley, and H. Cizkova (2017), Stress memory effect in viscoelastic stagnant lid convection, doi: 10.1093/gji/ggx102 (9) J.A. Olive, M.D. Behn, E. Mittelstaedt, G. Ito, and B.Z. Klein, The role of elasticity in simulating long-term tectonic extension, doi: 10.1093/gji/ggw044
