The Geodynamics 101 series serves to showcase the diversity of research topics and methods in the geodynamics community in an understandable manner. We welcome all researchers – PhD students to Professors – to introduce their area of expertise in a lighthearted, entertaining manner and touch upon some of the outstanding questions and problems related to their fields. This month we continue the conversation that was started at NetherMod 2017 by discussing how we initiate deformation in numerical models of the lithosphere and more importantly, does it matter how we start such models? Do you want to talk about your research? Contact us!
Geodynamic modelling often concerns itself with the study of localized deformation in the crust and lithosphere. The models generally start with an initial geometry, boundary conditions and a prescribed set of initial conditions that can be either thermal or mechanical. This initial setup is usually a standard representation of the lithosphere and asthenosphere, as inferred from geological and geophysical observations and laboratory rock experiments. The boundary conditions usually drive the deformation in the system. However, as a synthetic (computer) model is pristine at the start, the localization of deformation can take a long model time of up to millions of years, as numerical disturbances need to accumulate. Besides that, the deformation will likely localise near or at the boundary of the system because of the boundary conditions. In order to avoid this long starting phase, and to exert some control on the location of the initial deformation, several approaches are widely used to initiate and localize deformation. Examples of these are the S-point velocity discontinuity at the bottom of the system (e.g. Braun and Beaumont, 1995; Ellis et al., 1995; Willett, 1999; Beaumont et al., 2000; Buiter et al., 2006; Thieulot et al., 2008; Braun and Yamato, 2009) and the use of a weak seed. The latter are usually small zones that are weaker than the surrounding crust or lithosphere. As the lithosphere and crust are never homogeneous, using weak seeds in a model can be easily justified. They could represent regions of different material properties (e.g., heat production), inherited faults, inherited crustal thickness changes and/or plumes impacting the lithosphere. The popular NetherMod 2017 potatoes (yep, still referring back to that one. If you don’t know what this is about, check out this post) are an extreme case in which multiple weak seeds are used to reflect local geology. Traditionally, simpler, single weak seeds are used.
Here, I will give a brief (and by no means comprehensive) overview of the different weak seed methods used to initiate deformation in models of continental extension, and I will conclude with a discussion on how these different initial conditions affect the model evolution.
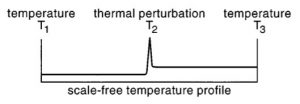
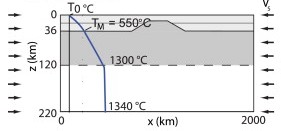
Modified figure from Burg & Podladchikov (1999): a thermal perturbation is used in the middle of their model to localise deformation there.
Seeding through thermal effects
The weak zone could be implemented as a temperature anomaly which could reflect a region in the crust of higher radiogenic heat production or a region in the lithosphere of locally reduced viscosity. They can be implemented by elevating the temperature or basal heat flux at the crust-lithosphere boundary or lithosphere-asthenosphere boundary with a certain amplitude over a finite region. Examples of studies using thermal weak seeds are Burg and Podladchikov (1999), Frederiksen and Braun (2001), Hansen and Nielsen (2003), and Brune and Autin (2013).
Seeding by mechanical inhomogeneity
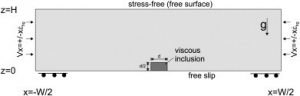
Modified figure from Kaus (2009): Model setup with a rectangular, viscous inclusion in the middle of the domain to initiate and localise deformation. Dimensions of the weak zone were varied, but maintained the aspect ratio 2:1.
A weak seed could be composed of a material with a lower rheological strength than its surroundings. There are multiple ways of achieving this, but often used methods include:
• A weak seed with a lower viscosity (e.g., Gray and Pysklywec, 2010; Gray and Pysklywec, 2012b; Gray and Pysklywec, 2012a; Kaus, 2009, and Mishin, 2011)
• A weak seed with a different angle of internal friction (e.g., Pysklywec et al., 2002; Kaus and Podlachikov, 2006; Thieulot, 2011; Gray and Pysklywec, 2013; Chenin and Beaumont, 2013)
• A weak seed with a different density (e.g., Tirel et al., 2008)
• A weak seed consisting of a different material (e.g., Pysklywec et al., 2000; Huismans and Beaumont, 2007)
• A weak seed with more accumulated strain than its surroundings (e.g., Lavier et al., 2000; Huismans et al., 2005; Warren et al., 2008a; Warren et al., 2008b; Petrunin and Sobolev, 2008; Beaumont et al., 2009; Allken et al., 2011; Kneller et al., 2013; Allken et al., 2013)
Apart from these different ways of making a seed weak, you can also find weak seeds of many different shapes and sizes in the literature. Most commonly, you will find
• Square weak seeds (e.g., Gray and Pysklywec, 2013)
• Rectangular weak seeds (e.g., Huismans et al., 2005) with different aspect ratios
• Fault-shaped weak seeds (e.g., Currie et al., 2007, and Currie and Beaumont, 2011)
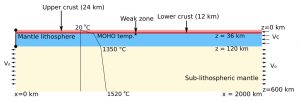
Modified from Gray & Pysklywec, 2013: Model setup with a square, frictionally weak zone of dimensions 10×10 km.
Seeding through geometrical discontinuity
Another method to create a zone of different rheological strength is by varying the thickness of the crust or lithosphere. A thickened lithosphere could represent a remnant of a previous mountain building phase, whereas a thinned lithosphere would represent a remnant of a previous rifting phase. Studies using this method of weakening include Gac et al. (2014) and Burg and Schmalholz (2008).
Influence of weak seeds on the model evolution
As mentioned at NetherMod 2017, you would ideally either have a generic model for which you should determine the influence of different initial weak seeds to check how robust your model is, or you would have a region-specific model for which you find the optimal initial conditions to get your desired model output. Only few studies have investigated the former in detail. Dyksterhuis et al. (2013) found that a single weak seed typically produces symmetric narrow rifts; multiple seeds produce a wide rift; and an initial fault-shaped weak zone produces an asymmetric rift.
It also raises the question about whether or not there are differences between similar codes when the same initiation method is used.
To shine a very preliminary light on this problem, I ran some models of continental extension using the SULEC and ELEFANT codes with different initial conditions. As both codes are based on the same physics, and have similar implementation, they should show a high degree of similarity when using the same deformation initiation method. The results show that different initiation methods indeed result in different results, particularly with respect to the timing of the deformation (see figure below). Besides that, SULEC tends to show more asymmetric behaviour than ELEFANT. For a more complete overview of the results and the model setup, please look here (my old (first!) poster for GeoMod 2014).

Models of continental extension after 10 Myr of extension for SULEC (top) and ELEFANT (bottom) for different initial, frictionally weak, weak seeds with aspect ratios of 6×6 elements, 12×3 elements, and 3×12 elements (i.e., the weak seed consists of the same amount of elements in each model).
In conclusion, I hope to add to the discussion of ‘how we start our models’ with this post by affirming that the model evolution is affected by our choice of weak seed (if only by the amount of waiting until deformation starts) and its effect can differ slightly between codes, even if the codes are very similar. Taking into account the vast variability of methods to initiate deformation, one really should be careful when assessing model results.
References Allken, V., Huismans, R., Fossen, H., and Thieulot, C. (2013). 3D numerical modelling of graben interaction and linkage: a case study of the Canyonlands grabens, Utah. Basin Research. Allken, V., Huismans, R., and Thieulot, C. (2011). Three-dimensional numerical modeling of upper crustal extensional systems. Journal of Geophysical Research, page doi:10.1029/2011JB008319. Beaumont, C., Jamieson, R., Butler, J., and Warren, C. (2009). Crustal structure: A key constraint on the mechanism of ultra-high-pressure rock exhumation. EPSL, 287:116-129. Beaumont, C., Munoz, J., Hamilton, J., and Fullsack, P. (2000). Factors controlling the alpine evolution of the central pyrenees inferred from a comparison of observations and geodynamical models. Journal of Geophysical Research, 105:8121-8145. Braun, J. and Beaumont, C. (1995). Three-dimensional numerical experiments of strain partitioning at oblique plate boundaries: Implications for contrasting tectonic styles in the southern Coast Ranges, California, and central South Island, New Zealand. Journal of Geophysical Research, 100(B9):18,059-18,074. Braun, J. and Yamato, P. (2009). Structural evolution of a three-dimensional, finite-width crustal wedge.Tectonophysics, 484:181-192. Brune, S. and Autin, J. (2013). The rift to break-up evolution of the Gulf of Aden: Insights from 3D numerical lithospheric-scale modelling. Tectonophysics, 607(0):65-79. The Gulf of Aden rifted margins system: Special Issue dedicated to the YOCMAL project (Young Conjugate Margins Laboratory in the Gulf of Aden). Buiter, S., Babeyko, A., Ellis, S., Gerya, T., Kaus, B., Kellner, A., Schreurs, G., and Yamada, Y. (2006). The numerical sandbox: comparison of model results for a shortening and an extension experiment. Analogue and Numerical Modelling of Crustal-Scale Processes. Geological Society, London. Special Publications, 253:29-64. Burg, J.-P. and Podladchikov, Y. (1999). Lithospheric scale folding: numerical modelling and application to the Himalayan syntaxes. International Journal of Earth Sciences, 88(2):190-200. Burg, J.-P. and Schmalholz, S. (2008). Viscous heating allows thrusting to overcome crustal-scale buckling: Numerical investigation with application to the Himalayan syntaxes. Earth and Planetary Science Letters, 274(1):189-203. Chenin, P. and Beaumont, C. (2013). Influence of offset weak zones on the development of rift basins: Activation and abandonment during continental extension and breakup. JGR, 118:1-23. Currie, C. and Beaumont, C. (2011). Are diamond-bearing Cretaceous kimberlites related to low-angle subduction beneath western North America. EPSL, 303:59-70. Currie, C., Beaumont, C., and Huismans, R. (2007). The fate of subducted sediments: a case for backarc intrusion and underplating. Geology, 35(12):1111-1114. Dyksterhuis, S., Rey, P., Mueller, R., and Moresi, L. (2013). Effects of initial weakness on rift architecture. Geological Society, London, Special Publications, 282:443-455. Ellis, S., Fullsack, P., and Beaumont, C. (1995). Oblique convergence of the crust driven by basal forcing: implications for length-scales of deformation and strain partitioning in orogens. Geophys. J. Int., 120:24-44. Frederiksen, S. and Braun, J. (2001). Numerical modelling of strain localisation during extension of the continental lithosphere. Earth and Planetary Science Letters, 188(1):241-251. Gac, S., Huismans, R. S., Simon, N. S., Faleide, J. I., and Podladchikov, Y. Y. (2014). Effects of lithosphere buckling on subsidence and hydrocarbon maturation: A case-study from the ultra-deep East Barents Sea basin. Earth and Planetary Science Letters, 407:123-133. Gray, R. and Pysklywec, R. N. (2010). Geodynamic models of archean continental collision and the formation of mantle lithosphere keels. Geophysical Research Letters, 37(19). Gray, R. and Pysklywec, R. (2012a). Geodynamic models of mature continental collision: Evolution of an orogen from lithospheric subduction to continental retreat/delamination. JGR, 117(B03408). Gray, R. and Pysklywec, R. N. (2012b). Influence of sediment deposition on deep lithospheric tectonics. Geophysical Research Letters, 39(11). Gray, R. and Pysklywec, R. (2013). Influence of viscosity pressure dependence on deep lithospheric tectonics during continental collision. JGR, 118. Hansen, D. and Nielsen, S. (2003). Why rifts invert in compression. Tectonophysics, 373(1):5-24. Huismans, R. and Beaumont, C. (2007). Roles of lithospheric strain softening and heterogeneity in determining the geometry of rifts and continental margins. Geological Society, London, Special Publications, 282(1):111-138. Huismans, R., Buiter, S., and Beaumont, C. (2005). Effect of plastic-viscous layering and strain softening on mode selection during lithospheric extension. Journal of Geophysical Research, 110:B02406. Kaus, B. (2009). Factors that control the angle of shear bands in geodynamic numerical models of brittle deformation. Tectonophysics, 484(1), 36-47. Kaus, B. and Podlachikov, Y. (2006). Initiation of localized shear zones in viscoelastoplastic rocks. Journal of Geophysical Research: Solid Earth 111.B4. Kneller, E. A., Albertz, M., Karner, G. D., , and Johnson, C. A. (2013). Testing inverse kinematic models of paleocrustal thickness in extensional systems with high- resolution forward thermo-mechanical models. Lavier, L., Buck, W., and Poliakov, A. (2000). Factors controlling normal fault offset in an ideal brittle layer. 105(B10):23,431--23,442. Mishin, Y. (2011). Adaptive multiresolution methods for problems of computational geodynamics. PhD thesis, ETH Zurich. Petrunin, A. and Sobolev, S. (2008). Three-dimensional numerical models of the evolution of pull-apart basins. Physics of the Earth and Planetary Interiors, 171:387-399. Pysklywec, R., Beaumont, C., and Fullsack, P. (2000). Modeling the behavior of continental mantle lithosphere during plate convergence. Geology, 28(7):655-658. Pysklywec, R., Beaumont, C., and Fullsack, P. (2002). Lithospheric deformation during the early stages of continental collision: Numerical experiments and comparison with South Island, New Zealand. JGR, 107(B72133). Thieulot, C., Fullsack, P., and Braun, J. (2008). Adaptive octree-based finite element analysis of two- and three-dimensional indentation problems. Journal of Geophysical Research, 113:B12207. Thieulot, C. (2011). FANTOM: two-and three-dimensional numerical modelling of creeping flows for the solution of geological problems. Physics of the Earth and Planetary Interiors, 188(1):47-68. Tirel, C., Brun, J.-P., and Burov, E. (2008). Dynamics and structural development of metamorphic core complexes. Journal of Geophysical Research: Solid Earth (1978-2012), 113(B4). Warren, C., Beaumont, C., and Jamieson, R. (2008a). Formation and exhumation of ultra-highpressure rocks during continental collision: Role of detachment in the subduction channel. Gcubed. Warren, C., Beaumont, C., and Jamieson, R. (2008b). Modelling tectonic styles and ultra-high pressure (UHP) rock exhumation during the transition from oceanic subduction to continental collision. EPSL, 267:129-145. Willett, S. D. (1999). Rheological dependence of extension in wedge models of convergent orogens. Tectonophysics, 305:419--435.