Building the Earth in a sandbox The Main Ethiopian Rift stretches for hundreds of kilometers through Ethiopia, a massive fracture where Africa is slowly tearing apart to birth a new ocean. However, the processes driving this continental breakup remain hidden deep beneath layers of volcanic rock and millions of years of geological history. Today, in a laboratory in the heart of the be ...[Read More]
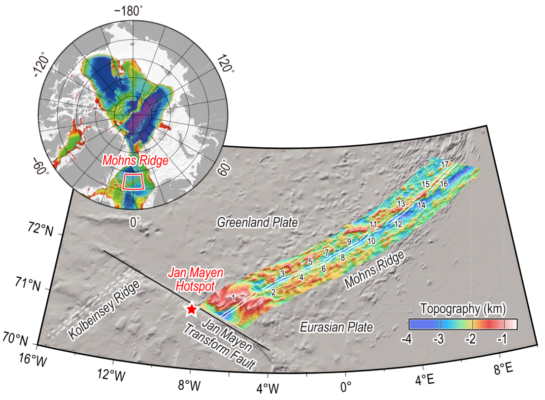
Mid-ocean ridges (MOR) and hotspots are two types of magmatic activity occurring in the ocean. The MORs are typically associated with another tectonic feature—oceanic transform faults. While numerous studies have focused on the interactions within MORs, hotspots, and transform faults, there has been limited research on cases where a hotspot and a transform fault are located at the same end ...[Read More]
This week inaugurates a new series of posts: Geekology, fusion of geek and geology. In this section, we will try to unravel tips and tricks of programming applied to geodynamics, from new innovative libraries to good programming practices, interviews with geologists who code and more! To kick off the series, this week’s article is written in collaboration with Baptiste Bordet, doctoral resea ...[Read More]
This week we have the second part of Junjie Dong’s insightful blog on modeling the early Earth. Following the discussion (“Modeling the Early Earth: Idealization and its Aims I”) about the major early Earth questions and challenges in modeling early Earth, Junjie now explores the imprtance of modeling as a scientific endeavor. He presents how one could more effectively model the ...[Read More]
