All models are wrong, but some are useful – we all have heard this quote. But it raises several questions (including but not limited to) – What would a model of the entire world look like? Can you couple geodynamical models with climate and biological evolution models? Would these models be useful? In this week’s blog post, Timothy Gray, a PhD student from ETH Zürich is looking for answers to these questions, and sharing his experiences about doing a PhD in the field of Biogeodynamics.
Timothy Gray is a PhD student in the Geophysical Fluid Dynamics group at ETH Zürich. His research focuses on global scale mantle numerical modelling, and the effects of different tectonic styles on surface topography and bathymetry.
The mantle makes up around 84% of the Earth’s interior, and its dynamics are relatively well understood considering that we’ve never been there and can only infer what’s down there from geophysical data and surface rock records. Mantle convection models, such as ASPECT (Kronbichler et al. 2012) or StagYY (Tackley, 2008) can model the evolution of planets from their formation to the present day and beyond – does this satisfy us yet?
Well, no. There’s much more to the Earth than the mantle, what about the atmosphere? This problem is less well understood, as climate processes work on many different spatial and time scales that are inherently difficult to model. Nevertheless, it is possible to make models to describe the climate of a planet as a function of atmospheric composition, continent distribution, and a number of other factors. Still, we might not yet be satisfied with this, as we have not incorporated a key system of Earth – life.
A recent development in the field of biology is the use of landscape ecology models – the use of models to predict the distribution of species as a function of their habitat. Conceptually, these models are somewhat like a much more advanced version of a cellular automata – cell based models are known for their ability to generate complex structures from a set of seemingly simple rules. Adding landscape ecology into the mix now gives us a much more complete model of the Earth, but how do we go about doing this?
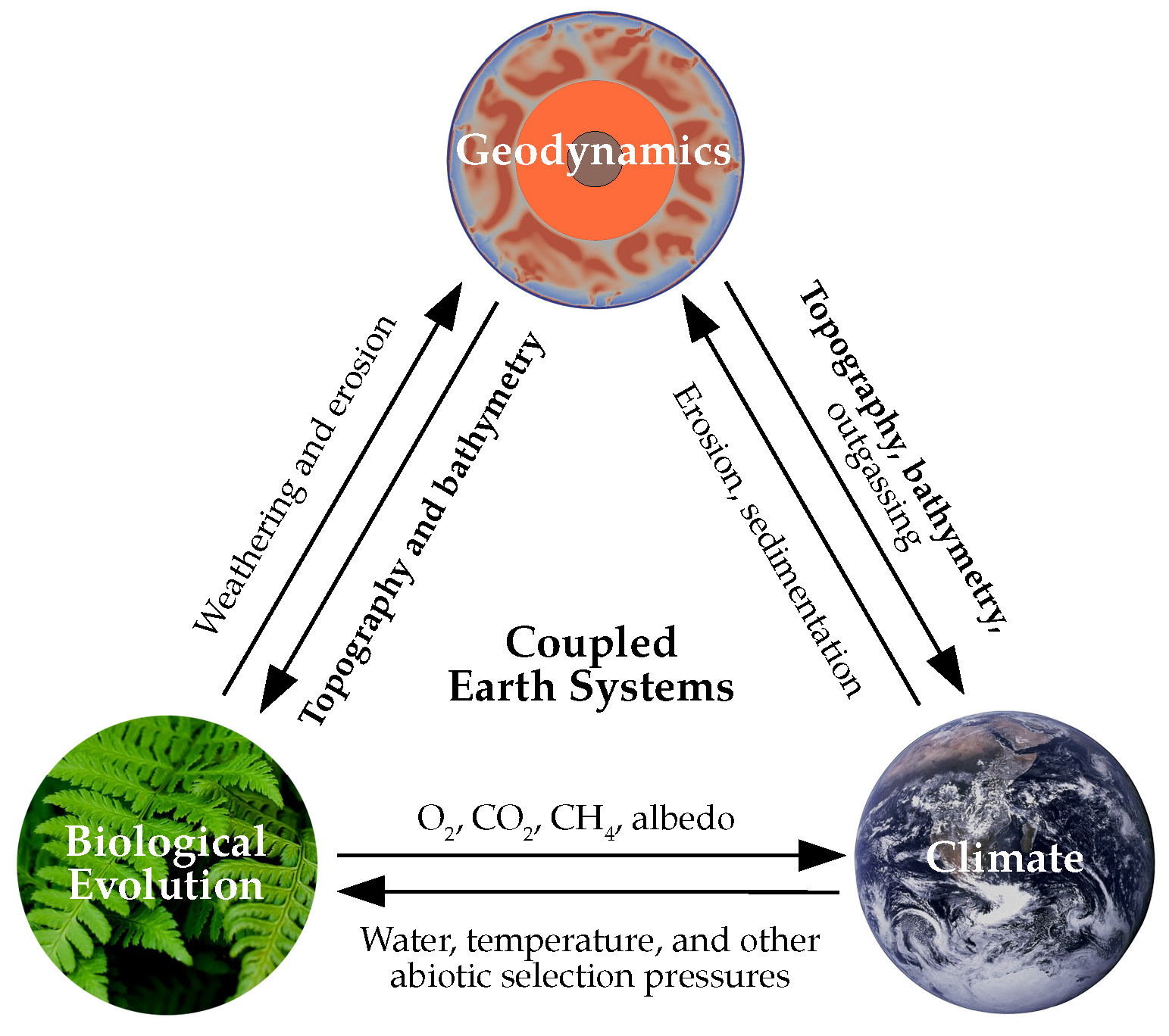
These three fields, geodynamics, climate, and biological evolution (Figure 1), all involve long time scales that are broadly compatible with one another. The Wilson cycle operates on the order of hundreds of millions of years, biological evolution on the order of millions. While we can’t reasonably model climate over millions of years directly (after all, it’s still difficult to model the weather next week), snapshots can be taken at various times and a kind of “average” climate can be inferred. There are a number of couplings between these fields that can be considered, and these are a topic of interest in the Biogeodynamics project at ETH, under the supervision of principal investigator Taras Gerya.
Figure 1 – Three coupled Earth systems – geodynamics, climate, and biological evolution.
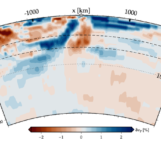
The most critical of these couplings, arguably, is the impact of topography and bathymetry, and their evolution over time. Earth’s climate today is largely a function of the configuration of continents and oceans. Imagine that the Earth had the same topographic evolution as Venus (Figure 2) – clearly the planet would have a radically different set of climatic zones due to the different configuration of land and ocean, and life (if it could exist at all) would evolve in a dramatically different fashion. The evolution of these systems over time would also be affected – a number of features of Earth’s climate and life are themselves direct consequences of reconfiguration of the surface over time, which would not be present on a stagnant planet.
Figure 2 – Earth with Venus’s topography. Credit: NASA.
https://www.nasa.gov/centers-and-facilities/giss/nasa-climate-modeling-suggests-venus-may-have-been-habitable/
The conclusion from this is that in order to successfully couple geodynamical models with climate and biological evolution, it is essential to accurately track the evolution of the surface over time.
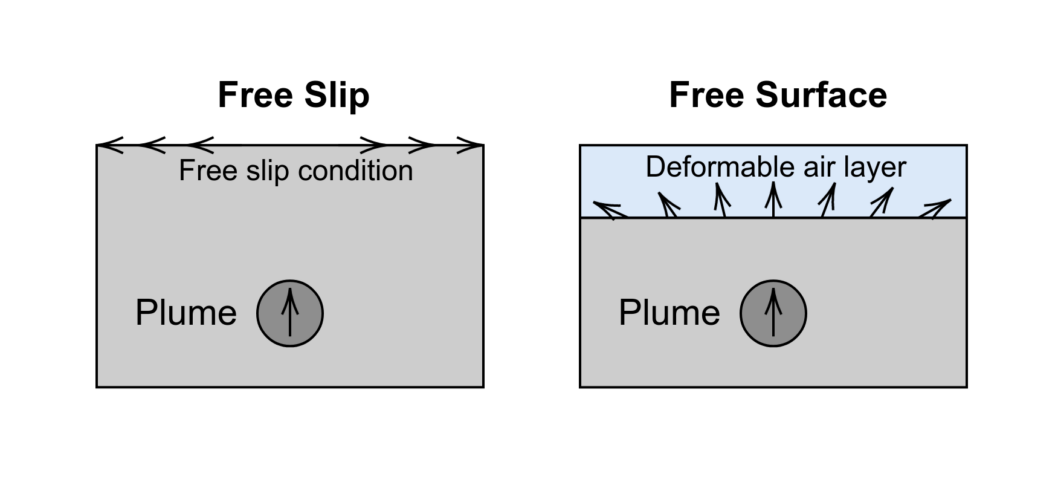
This brings us to my own research. I look at geodynamic models, in particular the code StagYY (Tackley, 2008), and investigate ways to model free surfaces (Figure 3). A free surface is a surface that is able to deform freely in response to stresses, as opposed to a more commonly used free slip condition where the location of the surface is fixed at the top of the model, and topography has to be inferred from the stress state. A free surface is the most natural top boundary condition for the top surface of a geodynamic model, and can enable some physics that is not possible with a free slip condition, but is unfortunately more difficult to implement (Crameri et al., 2012).
Figure 3 – The free surface boundary condition enables realistic surface deformation
Without getting into too many technical details (feel free to contact me if you are into those!), I have implemented a new discretisation method for the governing equations of mantle convection that produces the correct free surface condition at the surface through the use of cellwise rock volume fractions (Larionov et al. 2017). The rock volume fractions may be produced in one of several ways; I have implemented two such methods: a direct Lagrangian method, and the Volume of Fluid method (López & Hernández, 2022). The new method avoids the need for a low viscosity “sticky air” layer that is typically used in geodynamic models.
The result of this implementation of the free surface boundary condition is the ability to obtain more accurate and performant topographic evolution over long time periods in geodynamic models. This, along with other work being undertaken as part of the Biogeodynamics project, is helping us achieve our ultimate goal of coupling these fields. The future of modelling seems quite promising in this new, coupled direction – all models are wrong, but this one will be useful!
References:
Crameri, F., Schmeling, H., Golabek, G. J., Duretz, T., Orendt, R., Buiter, S. J. H., May, D. A., Kaus, B. J. P., Gerya, T. V., & Tackley, P. J. (2012). A comparison of numerical surface topography calculations in geodynamic modelling: An evaluation of the ‘sticky air’ method. Geophysical Journal International, 189(1), 38–54. https://doi.org/10.1111/j.1365-246X.2012.05388.x
Kronbichler, M., Heister, T., & Bangerth, W. (2012). High accuracy mantle convection simulation through modern numerical methods. Geophysical Journal International, 191(1), 12–29. https://doi.org/10.1111/j.1365-246X.2012.05609.x
Larionov, E., Batty, C., & Bridson, R. (2017). Variational stokes: A unified pressure-viscosity solver for accurate viscous liquids. ACM Transactions on Graphics, 36(4), 101:1–101:11. https://doi.org/10.1145/3072959.3073628
López, J., & Hernández, J. (2022). gVOF: An open-source package for unsplit geometric volume of fluid methods on arbitrary grids. Computer Physics Communications, 277, 108400. https://doi.org/10.1016/j.cpc.2022.108400
Tackley, P. J. (2008). Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid. Physics of the Earth and Planetary Interiors, 171(1), 7–18. https://doi.org/10.1016/j.pepi.2008.08.005
