The Asian continent has fascinated the world for at least 3,000 years with its music, food, and discoveries, as well as its breathtaking landscapes. Most of these incredible landscapes are formed by mountains that can be considered geologically “recent” (such as the Cenozoic formation of the Himalayas). However, there are also ancient terrains, pre-dating the Mesozoic, that pose intrig ...[Read More]
Building the Earth in a sandbox The Main Ethiopian Rift stretches for hundreds of kilometers through Ethiopia, a massive fracture where Africa is slowly tearing apart to birth a new ocean. However, the processes driving this continental breakup remain hidden deep beneath layers of volcanic rock and millions of years of geological history. Today, in a laboratory in the heart of the be ...[Read More]
In 2020, we found ourselves fully immersed in the world of virtual seminar series, a trend that has continued since then. By that time, the blog team made a compilation of seminar series of interest to the Geodynamics community. Four years have passed bringing both new additions and some that have become inactive. It’s now time for an update! Here is a non-exhaustive list of recorded seminar serie ...[Read More]
In this week’s blog post, one of our blog illustrators, Emily Hinshaw will take us on a journey to the faraway land of Alaska, which is well known for its rugged terrain, exciting wildlife, and being very remote. Despite these challenges, and many others, Emily loves this work and feels very lucky to be part of the research team which explores the geology and geodynamics of the region! Alaska is ...[Read More]
Dr. Anouk Beniest, an Assistant Professor in Tectonics at the Vrije Universiteit Amsterdamat, is an interdisciplinary earth scientist, bringing together geology, geophysics and geodynamics to help us understand complex geological problems. Her research revolves predominantly around plate tectonics, with a focus on extensional systems and she has kindly put together this blog post to convince you t ...[Read More]
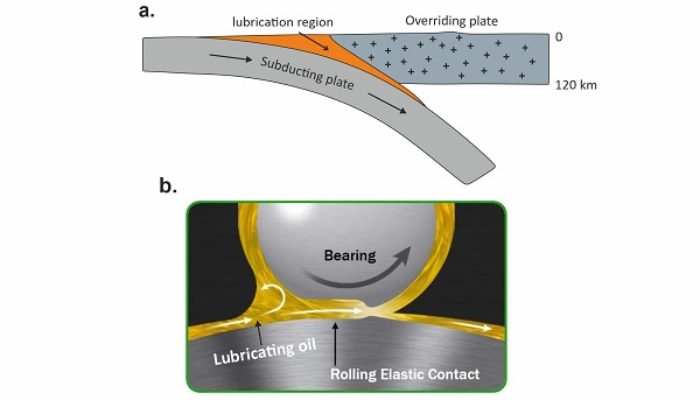
Plate interface lubrication is essential for stabilization and continuation of subduction process for million of years. The magnitude of plate interface lubrication determines transfer of stress between two converging plates, topography of mountain belts, transportation of volatiles to the mantle, and return flow of high to ultra-high pressure rocks to the earth’s surface. In this week’s blog, I ...[Read More]
Plume craton interaction is a fascinating geological phenomenon. The Indian plate, which has experienced several plume eruptions underneath it, is one of the best locations to study the effect of plume craton interaction. In this week’s news and view, I will provide an overview of the controversy and hypotheses related to the plume craton interaction within the Indian plate since the mid-Cre ...[Read More]
Science is all about discovering new things. But how do we make these discoveries, adding to the ever growing pantheon of knowledge? This week, we sit with one of our editors Antoniette Greta Grima, a Postdoctoral Fellow from the University of Texas at Austin, to understand what it takes to discover a new slab process. Thanks for sitting down with us this week! First things first, which subductio ...[Read More]
PhD students’ struggles are alike; each succeed in their own way[1] It was a Friday morning, and nearly 3 years had passed since I arrived at Sydney. This meant, I only had one month left to submit my thesis! No sooner had I entered my office than a feeling of anxiety had found me. I had no time to dig deep into my own thoughts to discover what was happening, although it was obvious. Instead, I re ...[Read More]
This weeks post is all about the importance of boundaries. Plate boundaries that is. Jean-Christophe Wrobel-Daveau and Graeme Nicoll tell us why we should care where plate boundaries are and how they evolve through time, when attempting to reconstruct past plate motions. Global plate tectonic models are an incredible way to synthesise geological knowledge to gain both direct and indirect insight i ...[Read More]