The central Mediterranean is a geodynamically complex region shaped by the interaction of multiple active subduction zones. In Italy, the central Apennines display a distinctive pattern of surface deformation that is proposed to be linked to a slab break-off beneath the area. In this week’s blog post, Maaike, a PhD student at ISTerre in Grenoble, …[Read More]
Every leadership transition marks the beginning of a new chapter, bringing fresh perspectives, new priorities and opportunities for growth. This year, the EGU Geodynamics Division warmly welcomes Professor Laetitia Le Pourhiet as its new president. A renowned researcher at the Institut Universitaire de France and Sorbonne Université, Prof. Le Pourhiet steps into the role with …[Read More]
Dear Geodynamics community, This is your trusted former Editor-in-Chief speaking. I have an important announcement! In very exciting news, the team behind the 101 Geodynamic modelling paper (which I am sure you have read and loved, right? No? Well, what are you waiting for?! Check it out here!) has reunited to write another very relevant …[Read More]
With the EGU General Assembly (GA) less than a month away, attendees should start planning their schedules to get the most out of the week. In today’s blog, Geodynamics (GD) Division Early Career Scientist (ECS) representative Garima Shukla highlights the GD Division’s networking events and provides an overview of key events at the GA. Networking …[Read More]
Hello fellow geodynamicists and geoscientists! Many exciting congresses and workshops are taking place this year. You might be going to some of them, so it’s definitely time to start planning your schedule. Don’t worry—we’ve got you covered! Here we collect events that might be of interest to you, with a focus on geodynamics and tectonics, …[Read More]
Subduction zones are dynamic regions where intense geological processes like earthquakes, volcanic eruptions, and the recycling of oceanic crust are constantly at play. A key factor that influences the behavior of these zones is *interface rheology*—the strength and viscosity of the boundary (the interface) between the subducting and overriding plates. Understanding this interface is crucial …[Read More]
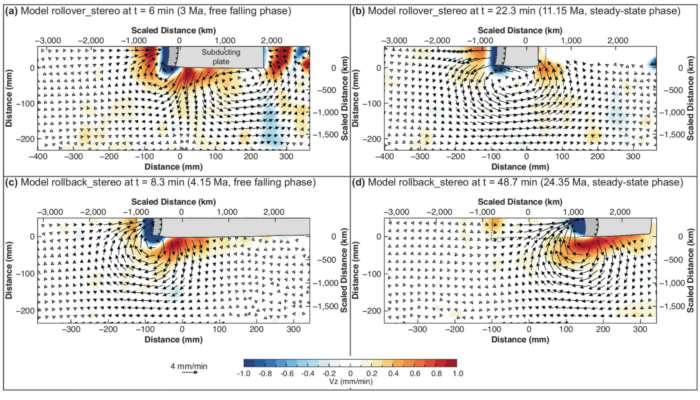
Geodynamic modelling helps us understand Earth’s internal processes by providing a framework to test hypotheses. Analogue modelling uses physical models governed by the laws of nature, with resolution down to Planck’s length. In contrast, numerical modelling employs mathematical methods to approximate solutions to the physical laws governing Earth’s processes. Each modelling approach comes with its …[Read More]
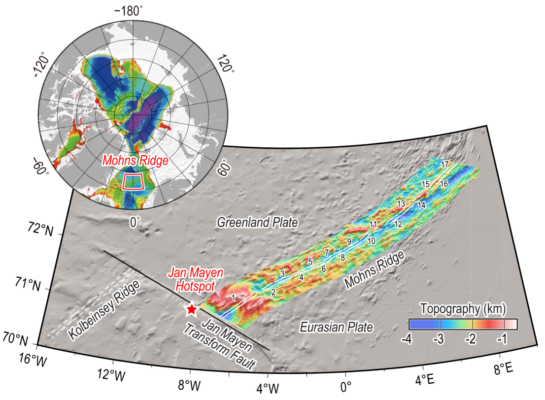
Mid-ocean ridges (MOR) and hotspots are two types of magmatic activity occurring in the ocean. The MORs are typically associated with another tectonic feature—oceanic transform faults. While numerous studies have focused on the interactions within MORs, hotspots, and transform faults, there has been limited research on cases where a hotspot and a transform fault …[Read More]
This week inaugurates a new series of posts: Geekology, fusion of geek and geology. In this section, we will try to unravel tips and tricks of programming applied to geodynamics, from new innovative libraries to good programming practices, interviews with geologists who code and more! To kick off the series, this week’s article is written …[Read More]
Ganymede, one of the Galilean moons of Jupiter and the largest in the Solar System, has caught the scientists’ attention due to its potential for hosting life. The JUICE mission, launched from the Guiana Space Centre in French Guiana on 14 April 2023, is on its way to orbit and conduct experiments on the Galilean …[Read More]
