Has the ocean temperature risen again? Are you tired of dressing like an onion to adapt to 15 degrees of change in a day? Here we have a cooling question. Peter asks: If you had infinite funding, what would you do? Dear Peter, If I had infinite funding, you’d find me setting up my new office at the bottom of the Mariana Trench – because if you’re going big, might as well go seven miles deep, ...[Read More]
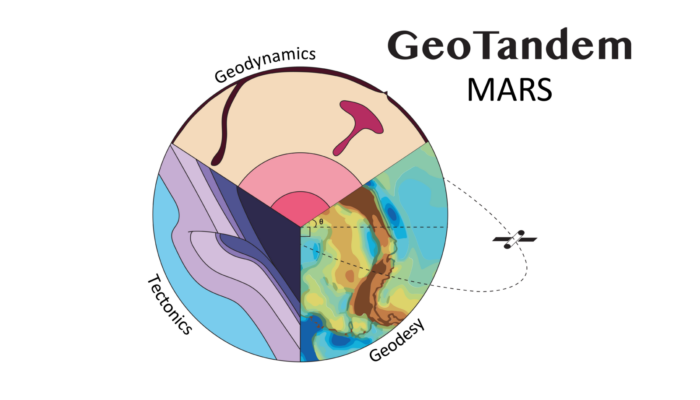
Geotandem: The Red Planet, often recognized as a dead planet, is not quite dead after all, at least geodynamically speaking
Welcome to the first of its kind, the Geotandem 01! A collaborative series between EGU divisions. Interdisciplinarity is intrinsic to Geosciences, so we want to showcase how researchers approach the same topics from different but also complementing perspectives. In each edition, we will bring you a high-interest topic for the community seen from the eyes of diverse disciplines. Today, the Tectonic ...[Read More]
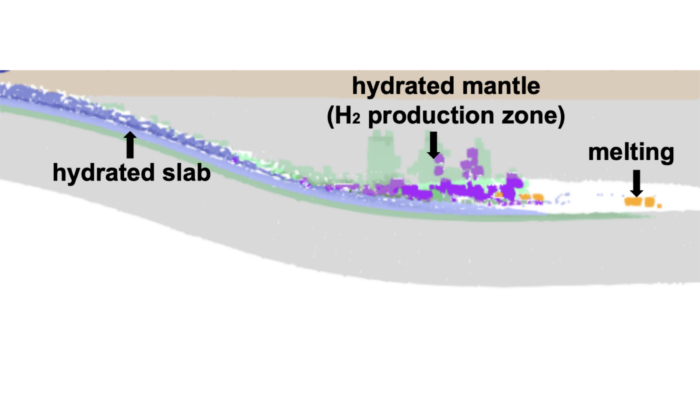
H2 production associated with mantle wedge hydration in subduction zones
Dihydrogen (H2) is a promising source of energy that may allow reducing carbon emissions in industry and transportation. Artificial production methods have been explored, natural sources of H2 (also called white dihydrogen) offer a more eco-friendly and cost-effective production process. In this week’s blog post, Alexis Gauthier, a PhD student from ISTeP, France, is discussing the H2 production pr ...[Read More]
Animating the past using numerical modeling
The human lifespan is too short compared to the geological time. To comprehend long-term phenomena, numerical modeling emerges as an imperative approach. But, there are several ways for visualizing the output of these models. Among these, animations stand out as a powerful tool, allowing us to watch the dynamic evolution of our planet over geological epochs like a movie. Our lives are too short co ...[Read More]