We are living in an anisotropic world. From rock-building crystals, ice, and trees growing in your garden to your favourite slice of cake many materials or objects has some anisotropic behaviour. What does this mean? Anisotropy (non-isotropy) implies that a material property depends on the direction of the measurement. In geodynamics we often talk about seismic anisotropy, originating from microsc ...[Read More]
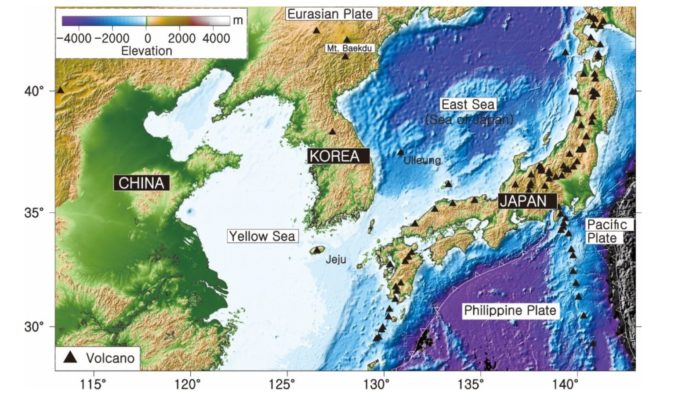
Northeast Asia may be one of the best natural laboratories to investigate both arc and intraplate volcanisms which have developed since the mid-Miocene. The arc volcanoes have occurred above the sinking young (Philippine) and old (Pacific) oceanic plates in Southwest and Northeast Japan subduction zones, respectively. The intraplate volcanoes across the Korean Peninsula and China have occurred abo ...[Read More]
Would you like to participate in the development of a completely new research field? Here is the opportunity – Biogeodynamics! Biogeodynamics is an emerging field with exciting research opportunities. In this blog post professors Taras Gerya, Loïc Pellissier, and Robert Stern talk about what is Bio-Geo-Dynamics, how this field is developing, and what are the challenges and opportunities ahead. A n ...[Read More]
The Tibetan Plateau is the most extensive elevated surface on the Earth, stretching ~1,000 km north to south and 3,200 km east to west, with a mean elevation of greater than 4.5 km and located north of the Indian subcontinent. The formation of this Plateau has profoundly influenced the variations and evolution of Asian climate, strengthening of the South-Asian Monsoon, development of the large Asi ...[Read More]
