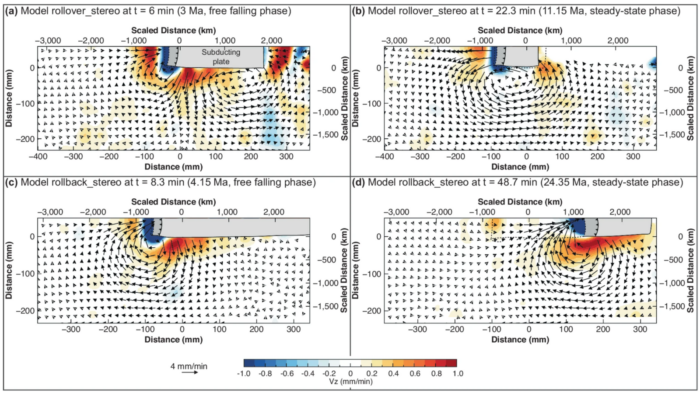
Geodynamic modelling helps us understand Earth’s internal processes by providing a framework to test hypotheses. Analogue modelling uses physical models governed by the laws of nature, with resolution down to Planck’s length. In contrast, numerical modelling employs mathematical methods to approximate solutions to the physical laws governing Earth’s processes. Each modelling approach comes with its own strengths and limitations, and making a choice between them is not always clear. To better understand this, I had the pleasure of speaking to Wouter Schellart about geodynamic modelling techniques and the rationale behind the use of both analogue and numerical modelling.

Wouter Schellart (https://orcid.org/0000-0002-9802-0143) is a Full Professor of Geodynamics and Tectonics in the Department of Earth Sciences at Vrije Universiteit Amsterdam. Currently in charge of the Kuenen-Escher Geodynamics Laboratory (KEG Lab) and leading the Geodynamics and Tectonics research group, his work primarily focuses on geodynamics and tectonics, using both analogue and numerical modelling techniques.
What are the pros and cons of analogue and numerical modelling?
- Investigating the progressive evolution of a particular geological or geodynamic process, providing a complete evolutionary picture of the process being investigated. In nature, many geological and geodynamic process occur over millions of years, such that their evolution is not directly observable.
- The particular geological or geodynamic process can be investigated in a controlled environment of the experimental laboratory or the virtual computer space.
- Geodynamic simulations allow the modeller to systematically investigate and quantify the influence of a particular physical parameter on a particular geodynamic process.
- Model results can be directly applied to the natural system to provide insight into the system in case the model is properly scaled.
- Last, but not least, running models, either in the lab or on a computer, can be great fun and exciting, for example when complicated processes unfold themselves live in front of your own eyes or when spectacular structures present themselves to you during a model run.
- Analogue models are actual physical experiments, so the physics is inherent to the system. In numerical models, physical processes are approximated with equations and numerical schemes.
- Analogue models are always four-dimensional (4D = 3D space + time), as experiments are always performed in three-dimensional space.
- Analogue models generally include a true free surface, as in most experimental set-ups the top surface is exposed to air.
- Parametric investigations are generally easy and straightforward to perform in numerical models. For example, investigating the influence of change in viscosity of a particular domain in your model on the geodynamic evolution only requires the modeller to change the viscosity value in the input file and run the model again.
- Extracting quantitative information from the numerical model, such as the velocity field, strain field or stress field, is straightforward and can generally be done at any location within the model domain.
- Numerical models are generally more flexible and allow more processes, set-ups or boundary conditions to be included or implemented than is possible in analogue models, although this is obviously code-dependent. For example, numerical models allow for the implementation of Cartesian, cylindrical and spherical geometry, while analogue models only allow for Cartesian geometry (and inverted cylindrical geometry for models performed in a centrifuge). Another obvious example is that numerical models allow for the implementation of metamorphic reactions and phase changes, while analogue models do not.
- Parametric investigations can be difficult in a number of cases. For those modelling investigations that involve changes in kinematics, such as the obliquity angle during rifting and the rate of convergence in accretionary wedge experiments, or geometry, such as the thickness of a particular strong or weak layer in the model, the parametric testing is straightforward. If the parametric study involves changes in material properties of a particular layer in the model, then complications can arise. For example, changing the viscosity of a particular layer in a model also changes the density of that layer, although generally by a small amount. In the ideal parametric investigation, only one parameter is changed at a time, not two or more.
- It is difficult to extract stress values directly from analogue experiments. It has been done in a number of cases, but the spatial distribution of stress measurements was generally limited to one or a few locations.
- As already stated above, in numerical models, physical processes are approximated with equations and numerical schemes.
- Large-scale numerical 4D modelling requires major computational resources.
In which cases is analogue modelling preferable to numerical modelling?
The modelling approaches are highly complementary and each has its own pros and cons
What are the major research themes and specific modelling cases currently being investigated by your research group?
Why are these approaches (analogue and numerical modelling) best suited for the specific cases you mentioned?
(…) geodynamic models are ideally suited to test the physical/dynamic viability of a particular conceptual model, idea or theory.
In your opinion, what does the future hold for analogue and numerical modelling, and how will they be used?
References Strak, V., Xue, K. & Schellart, W.P. Mantle upwelling induced by slab rollover subduction could explain widespread intraplate volcanism in Tibet. Commun Earth Environ 5, 510 (2024). https://doi.org/10.1038/s43247-024-01581-7