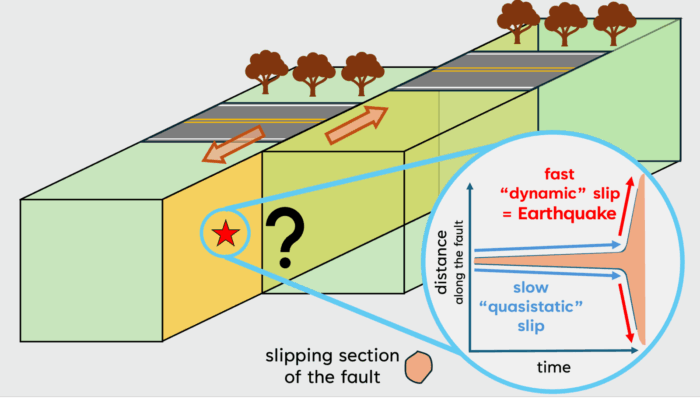
How do earthquakes start? Earthquakes occur when a block of rock rapidly slides past another along an interface or a discontinuity in the medium and release energy in the form of seismic waves. Turns out, the surface of the earth is riddled with a lot of these discontinuities, which we call “faults”. If we plot the locations of earthquakes on a world map (Figure 1a), we will see that they highlight the major plate boundary faults around the world (Figure 1b). You may have heard of the San Andreas fault in California or the megathrust beneath Japan, part of which ruptured during the magnitude 9.1 Tohoku earthquake in 2011, causing a massive tsunami. Even the highest mountains in the world have a tumultuous history (literally!) as their origin is related to the collision of two tectonic plates, one thrust over the other. The beauty of the Himalayas comes at the expense of devastating earthquakes. So, one thing we know is: earthquakes happen when faults slip. But how does this rapid slip start?
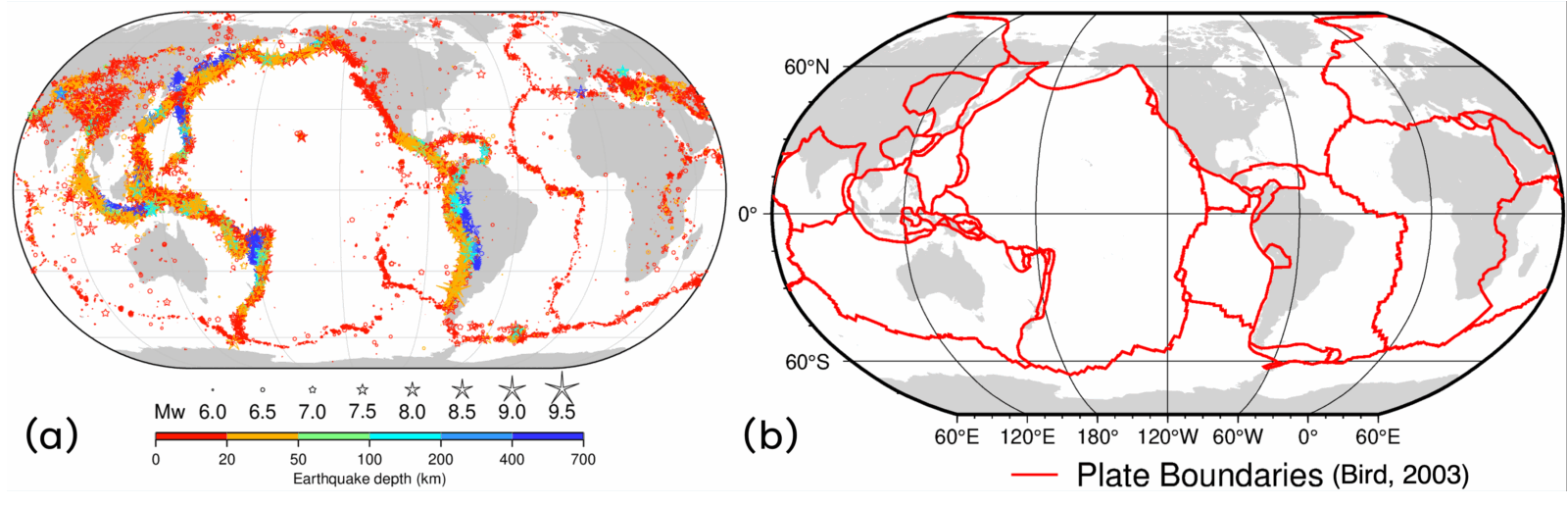
Figure 1. (a) Earthquakes around the world from 1904-2020 recorded in the ISC-GEM catalog (International Seismological Centre (2025)). (b) Major plate boundaries around the world (after Bird, 2003).
Fracture mechanics to the rescue!
Let’s start by thinking of an earthquake as slip along a frictional interface, in other words, a fracture. A good thing about that is: there is a whole field dedicated to studying discontinuities in materials. Fracture mechanics is all about how cracks initiate and grow. We can make things even simpler if we assume the medium is linear elastic, i.e. strain is linearly proportional to stress. By considering a crack as a slit-like discontinuity, we can determine the stress around the crack tip. One can then formulate criteria that govern crack growth based on the near-tip stress field. How earthquakes nucleate and propagate are important questions that earthquake scientists have attempted to answer under the framework of linear elastic fracture mechanics. Now, to move forward, we will need to understand how the frictional interfaces behave under stress.
Frictional laws: a little resistance goes a long way?
What controls the frictional resistance on an interface?
Let us go back to the classic spring and slider model, where we have a slider block attached to a spring, resting on a frictional interface, for instance, sandpaper. When we start pulling the spring, the motion of the block is resisted by the friction along the interface between the block and the sandpaper. As we pull with more and more force, we eventually overcome the frictional resistance and the block slides. This is a simplified analog of how slip happens along a fault. The fault is being stressed under tectonic loading and at some point, it slides (Figure 2). We can guess that the friction on the interface will be influenced by the material on either side, how smooth/rough the interface is, and whether there are any lubricants present (Bayart et al., 2016). For example: if we oil the interface, we can overcome the frictional resistance more easily.
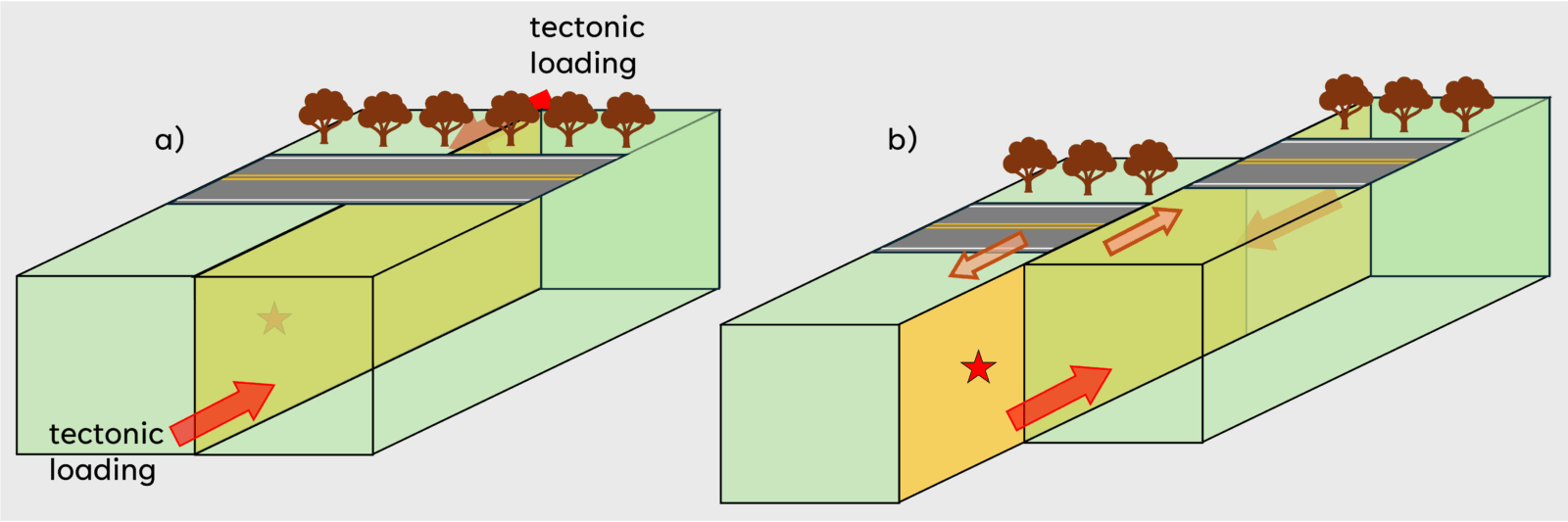
Figure 2. (a) A fault (planar surface in yellow) accumulates stress under tectonic loading (red arrows). (b) Once the stress exceeds the frictional strength, slip occurs. Smaller light brown arrows represent sense of slip.
What happens to the friction on an interface as it starts sliding?
A commonly used frictional law that tries to explain the frictional behavior along interfaces is the linear slip-weakening law. Once the shear stress on the interface exceeds its frictional strength, the interface begins sliding. The amount of stress on the interface decreases linearly as a function of slip until it reaches the residual stress after it slips a characteristic length scale (Ida, 1972; Palmer & Rice, 1973). This length scale is called the slip-weakening distance (L) (Figure 3). Under the slip-weakening law, the frictional strength decreases with slip. When the interface slips more than the slip-weakening distance, strength is reduced to the residual strength. This law, however, is not sufficient to explain the full behavior of natural faults.
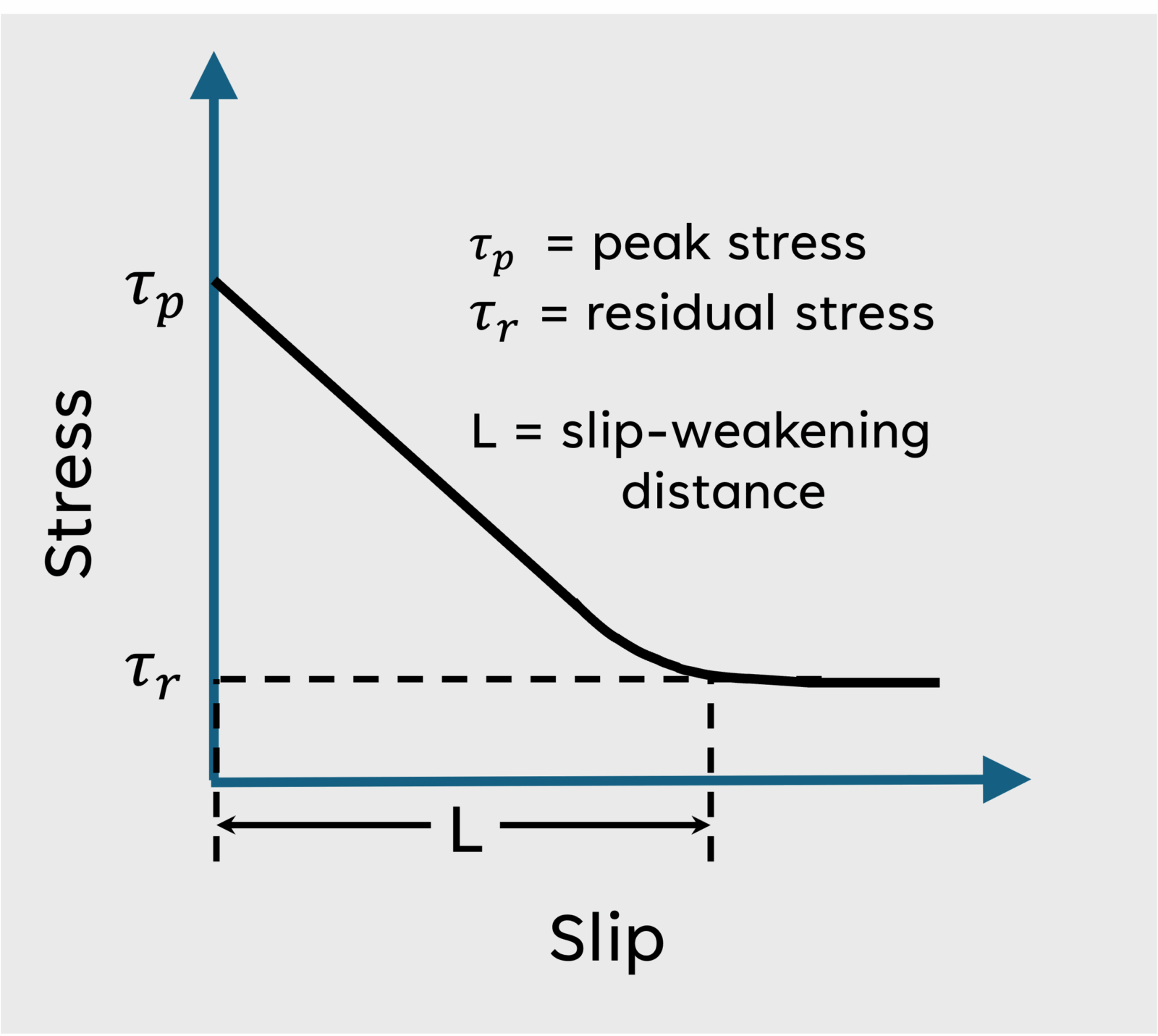
Figure 3. For the slip-weakening friction law, stress decreases from peak to residual over the slip-weakening distance (L) (figure adapted after Uenishi and Rice, 2003).
Rate- and state- friction law is a popular frictional law, which adds in more complexity than the slip-weakening law. It was formulated on the basis of velocity jump experiments in the laboratory, i.e. how the friction on the interface changes as the sliding velocity is changed (Dieterich, 1979; Ruina, 1983). As the name suggests, the friction coefficient depends both on the slip rate as well as the state of the fault (Dieterich, 1972, 1992; Ruina, 1983). The state can be thought of as the average time since contacts on the interface were formed (Dieterich, 1979). If the dynamic friction coefficient decreases with increase in velocity, the interface is velocity-weakening and otherwise velocity-strengthening (Figure 4). A velocity-strengthening system can slide stably (slowly without generating earthquakes) whereas a velocity-weakening system can transition from stable to unstable sliding, i.e. earthquake!
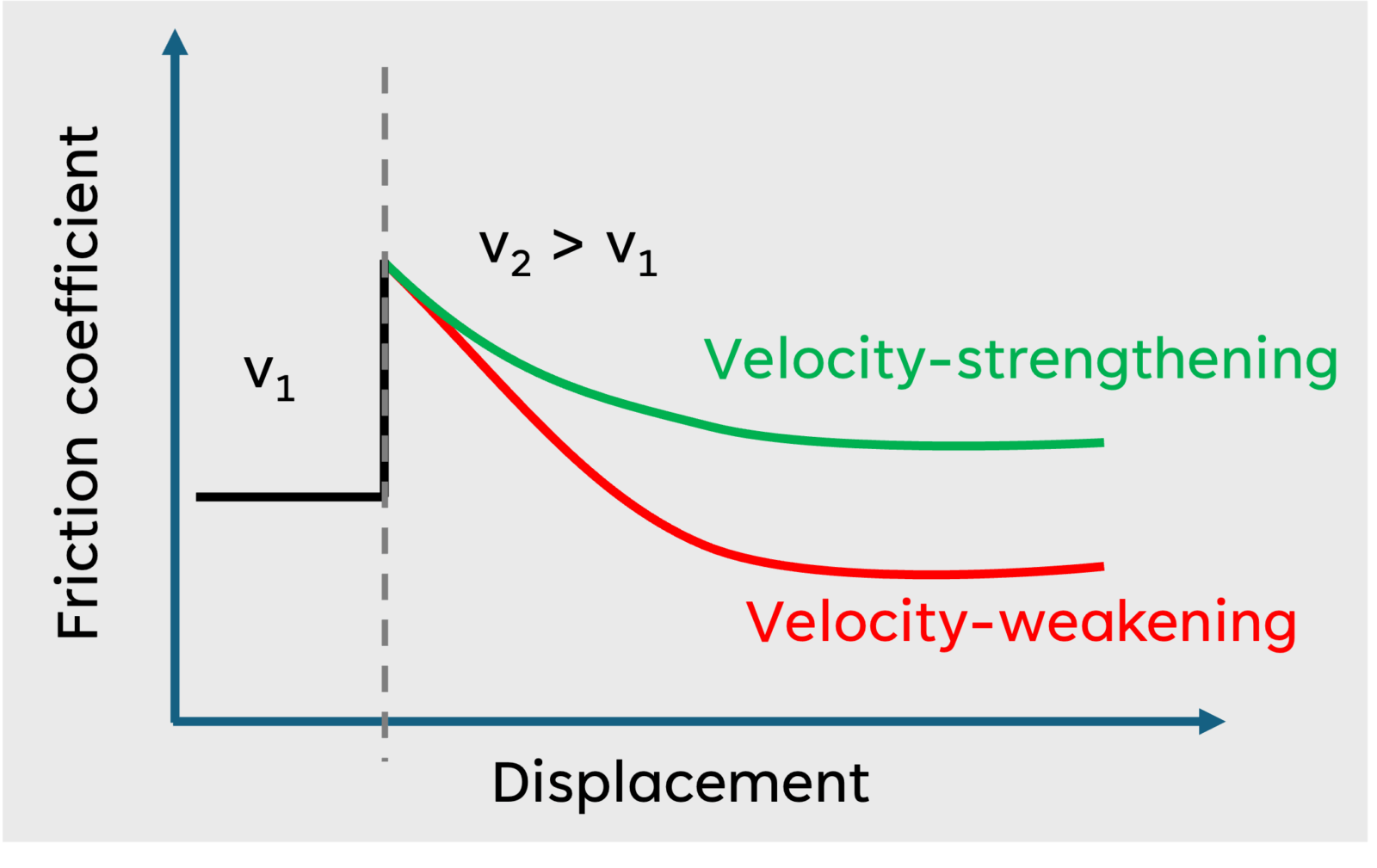
Figure 4. Velocity-strengthening and velocity-weakening behavior (figure adapted after Chen at al., 2024).
Critical nucleation length (h*)
A simple framework for rupture nucleation is that slip on an interface grows quasi-statically (without the generation of seismic waves) until a critical length scale for the slipping patch is reached. After that, the slip accelerates and grows dynamically into an earthquake. This critical length scale that marks the transition from slow, aseismic slip to fast, seismic slip is known as the critical nucleation length (h*). The nucleation phase of a fast rupture has been observed in several lab studies (Gvirtzman & Fineberg, 2021; Latour et al., 2013; McLaskey, 2019; Yamashita et al., 2021) and measurements of the nucleation length have been made. The critical nucleation length is influenced by the frictional properties of the interface, elastic properties of the material, and the effective normal stress (Rice et al., 2001; Rubin & Ampuero, 2005; Uenishi & Rice, 2003).
Under the slip-weakening friction law, estimates of the nucleation length has been determined by assuming that the nucleation happens before residual stress is reached on a homogeneous fault (Uenishi & Rice, 2003).
Under equilibrium, the stress on the fault is balanced by its frictional strength. By perturbing the velocity on the fault, we can determine the critical length scale that defines the transition to rapid, unstable sliding in the rate- and-state framework (Rubin & Ampuero, 2005).
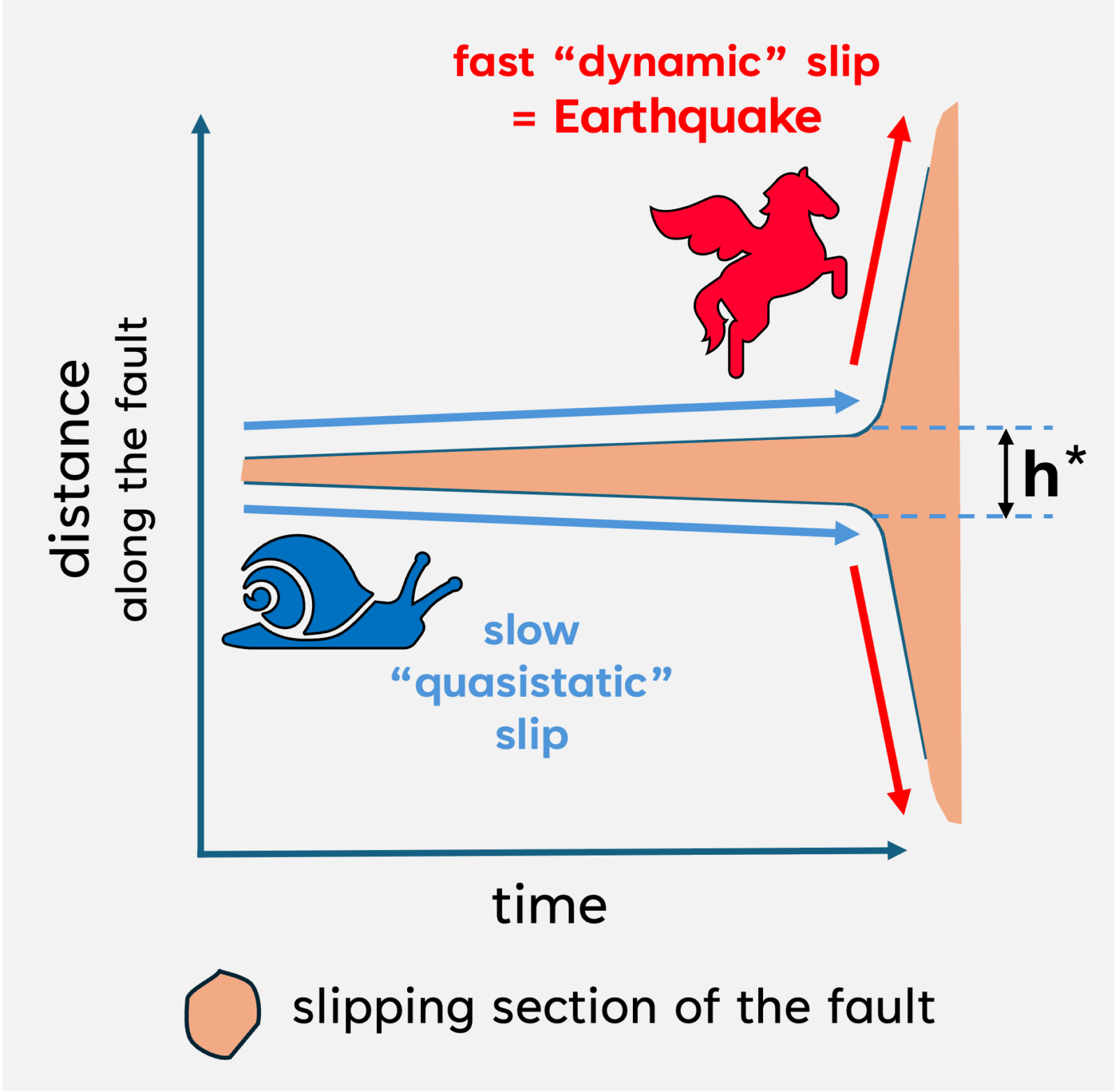
Figure 5. Slip grows quasi-statically on the fault (represented by blue arrows) before accelerating and transitioning into a dynamic rupture (red arrows). h* is the critical nucleation length.
Earthquake!! (the earth’s nervous breakdown?)
We have simplified the rupture nucleation scenario by assuming a fault with homogeneous frictional properties. For heterogeneous faults, the length scale of the asperities (frictional heterogeneities) can further influence nucleation. Multiple asperities can fail at once to initiate a rupture in addition to rupture growing from a single asperity on the fault (Lebihain et al., 2021). The presence of pressurized fluids along the fault will change the effective normal stress and therefore the nucleation length (e.g., Garagash & Germanovich, 2012). There are so many sources of complexities in nature. But the bottom line is – the earth can only hold so much, it cannot always stop itself from sliding (sigh!).
References Bayart, E., Svetlizky, I., & Fineberg, J. (2016). Slippery but Tough: The Rapid Fracture of Lubricated Frictional Interfaces. Physical Review Letters, 116(19), 194301. https://doi.org/10.1103/PhysRevLett.116.194301 Bird, P. (2003). An updated digital model of plate boundaries. Geochemistry, Geophysics, Geosystems, 4(3). https://doi.org/10.1029/2001GC000252 Chen, T.-W., Affinito, R., Marone, C., Fisher, D., Smye, A., & Hashimoto, Y. (2024). Frictional Properties and Healing Behavior of Tectonic Mélanges: Implications for the Evolution of Subduction Fault Zones. Journal of Geophysical Research: Solid Earth, 129(6), e2023JB028472. https://doi.org/10.1029/2023JB028472 Dieterich, J. H. (1972). Time-dependent friction in rocks. Journal of Geophysical Research (1896-1977), 77(20), 3690–3697. https://doi.org/10.1029/JB077i020p03690 Dieterich, J. H. (1979). Modeling of rock friction: 1. Experimental results and constitutive equations. Journal of Geophysical Research: Solid Earth, 84(B5), 2161–2168. https://doi.org/10.1029/JB084iB05p02161 Dieterich, J. H. (1992). Earthquake nucleation on faults with rate-and state-dependent strength. Tectonophysics, 211(1), 115–134. https://doi.org/10.1016/0040-1951(92)90055-B Garagash, D. I., & Germanovich, L. N. (2012). Nucleation and arrest of dynamic slip on a pressurized fault. Journal of Geophysical Research: Solid Earth, 117(B10), 2012JB009209. https://doi.org/10.1029/2012JB009209 Gvirtzman, S., & Fineberg, J. (2021). Nucleation fronts ignite the interface rupture that initiates frictional motion. Nature Physics, 17(9), 1037–1042. https://doi.org/10.1038/s41567-021-01299-9 Ida, Y. (1972). Cohesive force across the tip of a longitudinal-shear crack and Griffith’s specific surface energy. Journal of Geophysical Research (1896-1977), 77(20), 3796–3805. https://doi.org/10.1029/JB077i020p03796 International Seismological Centre (2025), ISC-GEM Earthquake Catalogue, https://doi.org/10.31905/d808b825 Latour, S., Schubnel, A., Nielsen, S., Madariaga, R., & Vinciguerra, S. (2013). Characterization of nucleation during laboratory earthquakes. Geophysical Research Letters, 40(19), 5064–5069. https://doi.org/10.1002/grl.50974 Lebihain, M., Roch, T., Violay, M., & Molinari, J.-F. (2021). Earthquake Nucleation Along Faults With Heterogeneous Weakening Rate. Geophysical Research Letters, 48(21), e2021GL094901. https://doi.org/10.1029/2021GL094901 McLaskey, G. C. (2019). Earthquake Initiation From Laboratory Observations and Implications for Foreshocks. Journal of Geophysical Research: Solid Earth, 124(12), 12882–12904. https://doi.org/10.1029/2019JB018363 Palmer, A. C., & Rice, J. R. (1973). The growth of slip surfaces in the progressive failure of over-consolidated clay. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 332(1591), 527–548. https://doi.org/10.1098/rspa.1973.0040 Rice, J. R., Lapusta, N., & Ranjith, K. (2001). Rate and state dependent friction and the stability of sliding between elastically deformable solids. Journal of the Mechanics and Physics of Solids, 49(9), 1865–1898. https://doi.org/10.1016/S0022-5096(01)00042-4 Rubin, A. M., & Ampuero, J.-P. (2005). Earthquake nucleation on (aging) rate and state faults. Journal of Geophysical Research: Solid Earth, 110(B11). https://doi.org/10.1029/2005JB003686 Ruina, A. (1983). Slip instability and state variable friction laws. Journal of Geophysical Research: Solid Earth, 88(B12), 10359–10370. https://doi.org/10.1029/JB088iB12p10359 Uenishi, K., & Rice, J. R. (2003). Universal nucleation length for slip-weakening rupture instability under nonuniform fault loading. Journal of Geophysical Research: Solid Earth, 108(B1). https://doi.org/10.1029/2001JB001681 Yamashita, F., Fukuyama, E., Xu, S., Kawakata, H., Mizoguchi, K., & Takizawa, S. (2021). Two end-member earthquake preparations illuminated by foreshock activity on a meter-scale laboratory fault. Nature Communications, 12(1), Article 1. https://doi.org/10.1038/s41467-021-24625-4
