
The crisis unfolding these days in Grindavík, Iceland reminds us of how important it is to forecast volcanic activity. Predicting the outcomes of volcanic unrest, or a magmatic intrusion making its way towards the surface, essentially amounts to three questions. Will there be an eruption? How much time before it starts? Where exactly will the eruption occur? Answering any of these questions is a daunting challenge. In this week’s post, I will focus on the last one.
Understanding magma pathways in the Earth’s crust

Dr. Lorenzo Mantiloni recently graduated from the GFZ and the University of Potsdam in Germany. His research interests include modelling of stress and magma pathways in the Earth’s crust and volcanic hazard assessment, as well as the dynamics and stability of magma reservoirs. He is currently a post-doctoral researcher at the University of Exeter in England. You can reach him by e-mail at l.mantiloni@exeter.ac.uk.
The locations where magma breaks through the Earth’s surface are known as eruptive vents. Forecasting where the next vent will form might sound easy for volcanoes with an open conduit or that regularly erupt from the summit, like Etna and Stromboli (Italy). Things get more complicated when the volcanic system has no central edifice, but rather a scattered distribution of past vents, like the Campi Flegrei caldera in Italy or the Auckland Volcanic Field in New Zealand. Even open-conduit volcanoes often experience flank eruptions, where magma travels long distances away from the centre of the edifice before breaching the surface. It is then essential to understand how magma propagates through the Earth’s crust and what drives it.
Most of magma transport in the Earth’s crust is accomplished by dykes: sheet-like intrusions with width and breadth much larger than their thickness. Dykes open their own pathways and can travel long distances in the crust in a few days or even hours, but often stop before reaching the surface. When they don’t, they can feed fissure eruptions, like the ones at Fagradalsfjall, Iceland in the last two years. Dykes account for most of crustal accretion at continental rifts and mid-ocean ridges, and contribute substantially to the building of volcanic edifices. Therefore, they play a significant role in shaping our planet – just more locally and on shorter timescales than most of geodynamic processes.
Dykes are commonly modelled as magma-filled tensile fractures: cracks that displace perpendicularly to their own surface. A long-spanning literature has established that if certain conditions are met, the stress concentration at the tip of the crack will overcome the host rock’s resistance to tensile fracturing, and the crack will advance. Such conditions arise from the competition between the crack’s internal pressure and the external load on the crack’s surface. As a result, dykes tend to open perpendicularly to the direction of the least-compressive principal stress axis. In fact, the simplest model of a dyke pathways is a streamline following the stress field in the host rock. However, dyke models have pushed way beyond that in the last decades (check out Rivalta et al., 2015 [1] for a nice review), accounting for mechanical layering in the host rock, magma buoyancy and viscous flow and describing either a dyke’s trajectory or its shape and velocity (to this day it is hard to do both). Nonetheless, until recently, most models were limited to 2D.
Reliable models of dyke pathways could be the key to forecasting where the next eruptive vents will open in a volcano. This idea was first explored by Rivalta et al. (2019) [2]. Combining a 2D model of stress and dyke pathways with a statistical framework, they used the distribution of past vents at the Campi Flegrei caldera to constrain the local stresses so that dykes starting from a known magma chamber would reach the locations of known vents. Then, based on the retrieved stresses, they ran more dyke simulations to estimate the probability of future vent opening with the distance from the caldera centre. Despite the simplicity of the models, it was a promising concept and called for further development. And that’s where my adventure as a fresh, unsuspecting PhD student at GFZ Potsdam (Section 2.1) began.
Modelling dyke pathways with SAM
The task at hand was clear. First, develop 3D models of dyke pathways and crustal stress that were both realistic and as fast and simple as possible. Next, integrate those tools into a probabilistic framework to constrain the state of stress and forecast future vent locations in existing calderas and, more generally, volcanoes. Back then, there was nothing of the sort around.
As a first step, I worked on numerical stress models. The state of stress in volcanoes results from the interplay of numerous processes, acting over very different space and time scales. I focused on those having the largest contributions: regional stresses due to tectonic activity and, more locally, the gravitational loading due to topography.
Fast forward one year, and a fully-3D numerical model of dyke pathways was developed by Davis et al., 2020 [3] & 2021 [4]. Unfortunately, as remarkable as it is, it was neither fast nor simple enough for my purposes. So, I turned back to the old 2D-streamline approach to see if it could be upgraded to 3D; and after a few wrong turns, SAM (Simplified Analytical Model of dyke pathways) was born.
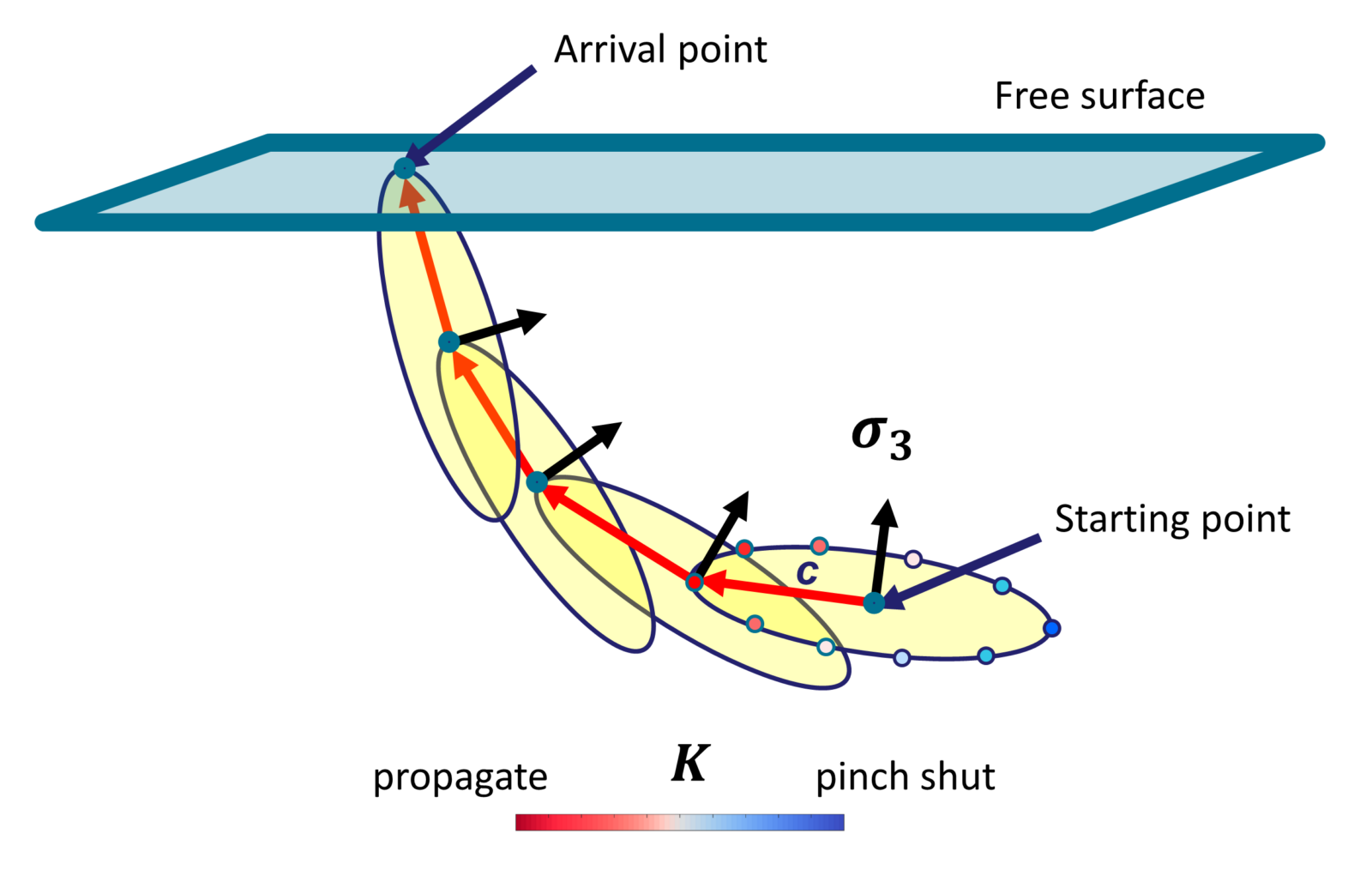
Figure 1: sketch of a SAM dyke. c: radius of the penny-shaped cracks. Black arrows: directions of least-compressive principal stress. Coloured dots represent the values of the stress intensity factor (K).
As the name says, SAM is a simple model, where the dyke is a penny-shaped crack with a fixed radius, forced to open perpendicularly to the direction of the least-compressive principal stress axis at its centre. The stress intensity factor (K), calculated along the crack’s tipline, determines the direction of propagation. K depends on the gradient of the magma buoyancy force and the external stress acting normally to the crack’s plane, and the point where it is largest becomes the centre of the next crack (Figure 1). Thus, a chain of points is produced, making up the dyke pathway. The most interesting feature of SAM is that, owing to its simplicity, it can also backtrack dyke trajectories from any point down through the crust. Finally, as the model is analytical, it is as fast as the stress model used to run it.
After much testing and benchmarking (Figure 2), I finally published SAM earlier this year (Mantiloni et al., 2023 [5]), and it is now available on GitHub. Nonetheless, the journey was far from over, as I had yet to devise the stress inversion and vent forecast framework. A few months in, the job is almost done, but that’s a story for another time.
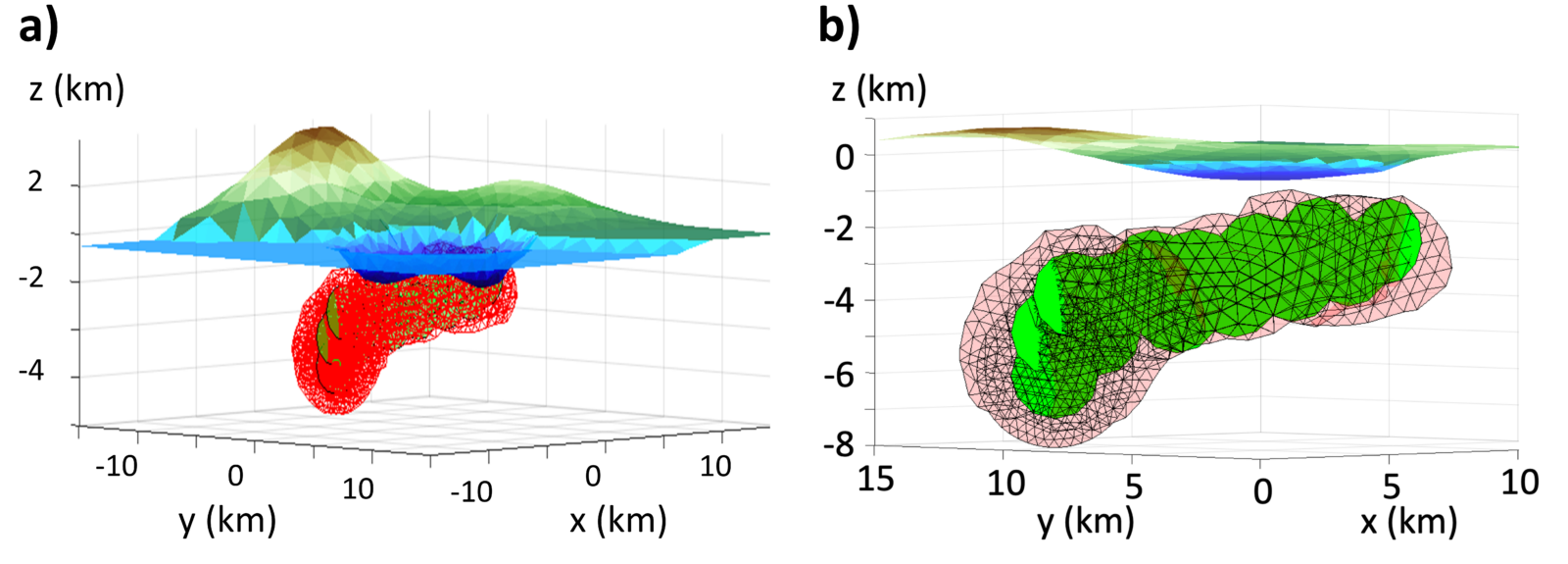
Figure 2: comparison between SAM (green cracks) and the numerical model by Davis et al. (2020) [3] (red triangles) in a synthetic scenario with a caldera lying on a coastline (a). Both dykes propagate laterally below a topographic high before stopping (b). Panel (b) is modified from Mantiloni et al. (2023) [5].
Limitations and perspectives
I finished my PhD last month, and now I have some time to mull over the frustrations and rewards that came with it. Two things have troubled me most. First, despite the complexity of the modelling, the setup of both SAM and the stress models remains relatively simple. For example, the models assume a linearly-elastic, homogeneous crust, which is obviously not the case for real rocks. They cannot say anything about a dyke’s velocity because they neglect the viscous flow of magma, whereas dyking is a dynamic process. Another limitation is the assumption that stress contributions of topographic features do not change with time, although there are many stress-altering factors out there – including dykes themselves. How dreadful! Secondly: SAM has only been tested on synthetic scenarios (Figure 3) and has yet to be (officially) tested on real data.
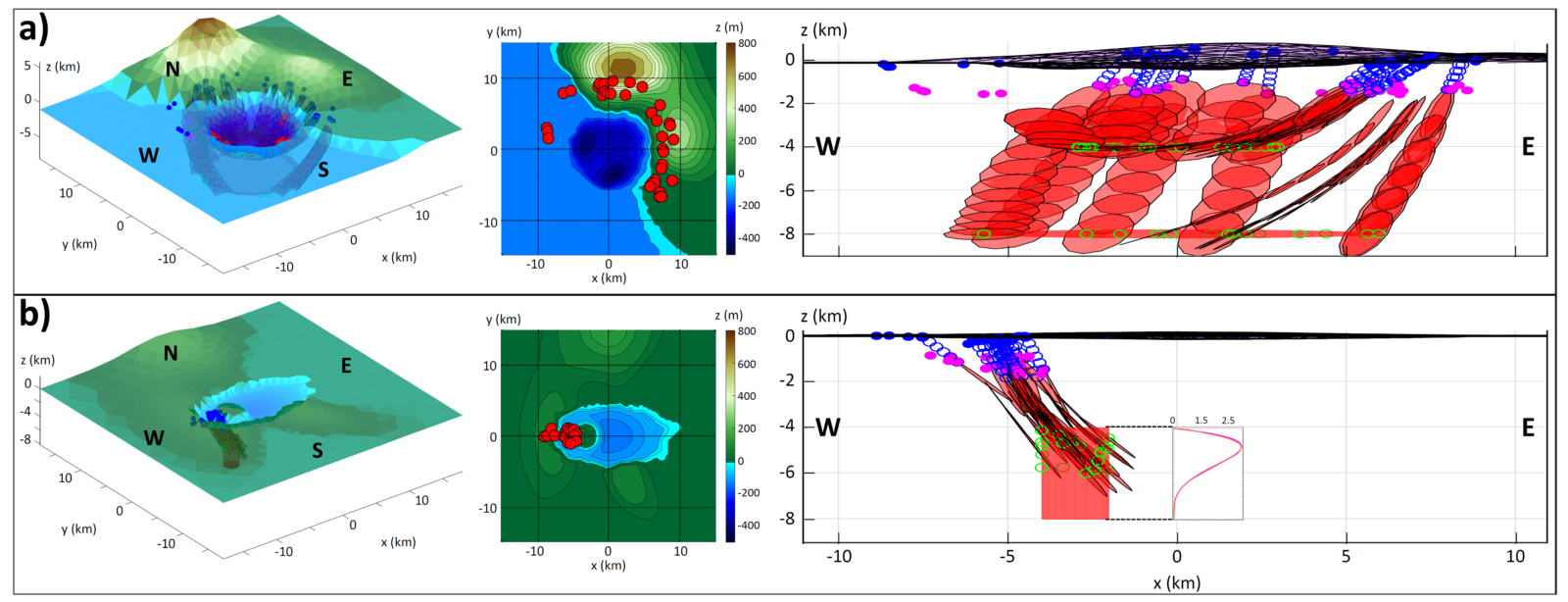
Figure 3: examples of SAM simulations in synthetic scenarios. The stress field is controlled by gravitational loading of topography and extensional tectonic stresses. (a): dykes depart from two sill-like reservoirs at different depths below the same caldera of Figure 2. (b): dykes depart from a vertically-elongated reservoir below an elliptic caldera with a resurgent dome. Modified from Mantiloni et al. (2023) [5].
On the dilemma of using “simple models” to explain complex natural processes
I was often faced with an existential question when immersed in my work as a geoscientist: how valid is my work to the real world when it mainly consists of manipulating theoretical models on a computer screen? My uncertainty on whether my research could have any practical applications in the future often let me wonder about the true extent of my contributions.
Coping with this dilemma took me a while, and missing the chance of connecting with other people during the pandemic years did not help. The first step in overcoming it was to accept the plain truth: nature is complex, models are not (as much). “Model” is a double-edged word: our only way to understand a natural process, share our understanding with others and make predictions about it, and, at the same time, an approximation of reality that can easily mislead us. If the model is sound and its parameters are accurately constrained, its predictions will also be accurate. Then, models need to be simple, because fewer parameters may be constrained with scarce data and are also easier to interpret physically. Of course, this entails some compromise: a model cannot be too simple, especially if we expect it to make complex predictions.
Simplicity demands assumptions …
… made by choosing what to include and what to leave out of a model. This requires determining what factors have the largest control on a process by forward modelling, and then focusing on those. Such was my approach to model the stress in volcanoes. The same applies when it comes to model dyke pathways, but in my case this was not all. SAM needed to operate fast, as it was designed for statistical applications, which involve running hundreds of thousands of simulations and extensive testing. Therefore, sophisticated numerical models were unsuitable, no matter how simple their setup was. From then on, I built SAM by only focusing on its required features. SAM should predict the arrival point of a dyke for a given starting point and stress field: then, knowing the dyke’s velocity was not necessary, and I could drop out the calculation of the viscous flow. Rocks in nature are heterogeneous, but constraining rock heterogeneity in my statistical framework would have been a nigh impossible task (again, there are too many free parameters). Thus, I made the assumption that the medium is homogeneous and let my stress inversion framework retrieve an “effective stress model” of the crust that may account for the neglected heterogeneities. The aim was not so much to reproduce the pathway of a specific dyke observed in the field, but rather to constrain the large-scale behaviour of dykes at different volcanoes.
My models would have been useless if they did not reproduce the patterns commonly observed in nature. Hence, the need to test them, possibly with real case studies. Instead, I opted for synthetic tests as a first step, since building a fast and efficient method to forecast magma pathways with SAM required a deep understanding of its limitations and sensitivity. The use of synthetic scenarios gave me full control over the variables, so that I could benchmark SAM with previous models. Furthermore, SAM is grounded on the same physics that has informed past dyke models in 2D, which have been widely applied to nature, and compares well with them.
Conclusion: Build your own pathway
When the pandemic receded and we could move around again, I realized that I wasn’t the only one struggling with the dilemma of simplicity. Since volcanoes are complex natural systems, assumptions have to be made and factors neglected, and yet many people out there are working on amazing models that can improve our understanding of volcanic activity. SAM strives for simplicity because it aspires to evolve into a practical forecasting tool for magma pathways that, if successfully tested in real cases, would have massive potential for future applications in risk and hazard assessment. For instance, it would help identifying the areas more susceptible to eruption and raise the population’s awareness of the risk long before the coming of the next dyke. In a crisis like the one in Grindavík, this would have made a huge difference.
Finally, I am confident that there will be plenty of opportunities to apply my model to real-world scenarios and demonstrate its practicality. There will be more challenges ahead, with their load of setbacks and rewards, but they are all a chance of advancing our knowledge. From all model trials and errors, I have learnt that pointing out the wrong paths is just as important as choosing the right one.
I dedicate this post to my PhD supervisor, Eleonora Rivalta. Her talent, passion and trust have made me grow from naive student to somewhat-less-naive researcher and realize the importance of simplicity. Without her, this post would have been twice as long.
References: [1] Rivalta, E., Taisne, B., Bunger, A. P., & Katz, R. F. (2015). A review of mechanical models of dike propagation: Schools of thought, results and future directions. Tectonophysics, 638, 1-42. https://doi.org/10.1016/j.tecto.2014.10.003 [2] Rivalta, E., Corbi, F., Passarelli, L., Acocella, V., Davis, T., & Di Vito, M. A. (2019). Stress inversions to forecast magma pathways and eruptive vent location. Science advances, 5(7), eaau9784. https://doi.org/10.1126/sciadv.aau9784 [3] Davis, T., Rivalta, E., & Dahm, T. (2020). Critical fluid injection volumes for uncontrolled fracture ascent. Geophysical Research Letters, 47(14), e2020GL087774. https://doi.org/10.1029/2020GL087774 [4] Davis, T., Bagnardi, M., Lundgren, P., & Rivalta, E. (2021). Extreme curvature of shallow magma pathways controlled by competing stresses: insights from the 2018 Sierra Negra eruption. https://doi.org/10.1029/2021GL093038 [5] Mantiloni, L., Rivalta, E., & Davis, T. (2023). Mechanical Modeling of Pre-Eruptive Magma Propagation Scenarios at Calderas. Journal of Geophysical Research: Solid Earth, 128, 3. https://doi.org/10.1029/2022JB025956




