The advance of Artificial Intelligence is impacting all spheres of human activity, and Geosciences are no exception. In this week’s post, Denise Degen from RWTH Aachen University, Germany, gives us a glimpse of what this means for Geodynamics. Discussing the advantages and caveats of different approaches, she shows how physics-based Machine Learning may help us investigating and understanding complex subsurface processes, as long as we take it with a grain of salt.

Denise Degen from RWTH Aachen University (Germany) is researching surrogate model construction for applications in Geodynamics.
At the latest after the recent developments around ChatGPT, the discussion about the role, risks, and opportunities machine learning poses is at a new high. The possibilities for machine learning seem to be endless, but the risks and concerns as well. Especially the aspect of how trustworthy these models are is a main discussion point. So, the question arises: is machine learning a curse or a blessing? A question that is not straightforward to solve, since the answers vary drastically for different fields. In this blog entry, we address it from a geodynamical perspective, detailing the requirements for machine learning in this scientific field along with its opportunities as well as open challenges.
Why surrogate models?
Before having a closer look at machine learning, we first have to answer the question of why we are interested in these techniques. Process simulations are widely established and recognized, so why should they be substituted? In Geodynamics, we face the challenge of describing nonlinear processes across different length and time scales (van Zelst et al., 2021 [1]). Additionally, we deal with observation data which are mostly available at the Earth’s surface and for present-day conditions. Thus, we obtain models with high uncertainties arising from structures, material properties, and unknown physical processes. Characterizing these uncertainties and understanding their impact often requires methods such as probabilistic uncertainty quantification and global sensitivity analysis (Degen et al., 2022 [2]; Degen et al., 2023 [3]). These methods share a high computational burden since they require numerous forward evaluations, yielding major challenges. Since already a single model evaluation often requires high-performance infrastructures, model evaluations in the order of a couple of hundred thousand to millions are prohibitive. Hence, the need for surrogate models: that is, lower-dimensional representations of the original model which are orders of magnitude faster to evaluate (Benner et al., 2015 [4]; Degen et al., 2023 [3]).
Why and when to use machine learning?
We illustrated the necessity for surrogate models, but that does not answer the question of which techniques are best suited to construct surrogate models for geodynamic applications. One method that comes to mind is machine learning. But how efficient and reliable are data-driven methods, in a field where we rely on physics and have mostly sparse data? Why do we not rely on physics-based methods for the construction of surrogate models that guarantee the preservation of physical laws? These methods exist, but work well and efficiently mostly in linear applications (Benner et al., 2015 [4]; Degen et al., 2023 [3]; Hesthaven et al., 2016 [5]), and are typically not efficient in the nonlinear setting, where data-driven methods such as neural networks are known to perform very well (Hesthaven et al., 2018 [6]). Hence, we would like a physics-based method that has the ability of data-driven methods to address nonlinear problems. This is where physics-based machine learning methods come into play (Figure 1). So, methods that try to combine the best of both worlds. Different physics-based machine learning methods exist: a prominent candidate is the physics-informed neural network (PINN) (Raissi et al., 2019 [7]), and a less well-known approach is the non-intrusive reduced basis (NI-RB) method (Hesthaven et al., 2018 [6]). Although both methods have the same aim, they differ conceptually. In the following, we explain how these conceptual differences affect geodynamic applications.
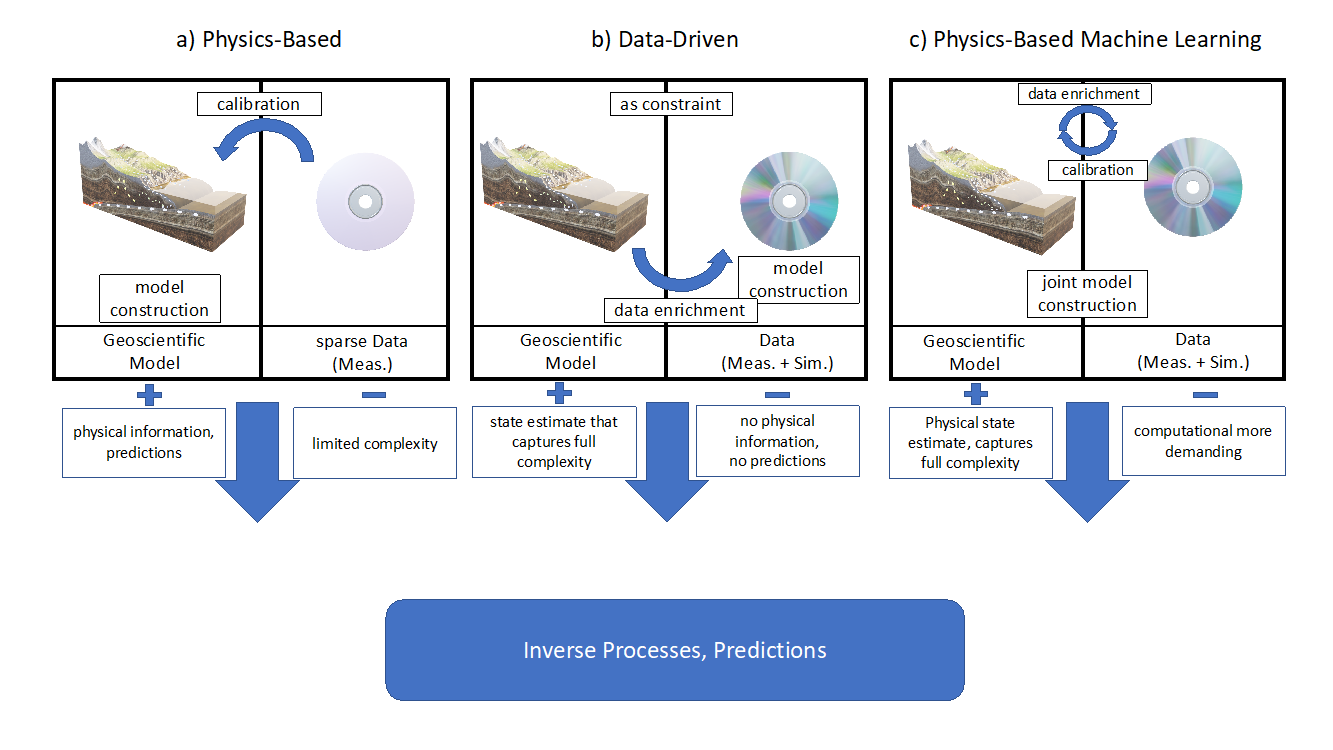
Figure 1: Schematic representation of the various classes of surrogate model construction techniques (Figure from Degen et al., 2023 [3]).
Black Box Approaches
The major conceptual difference between PINNs and the NI-RB method is the way they integrate physics. In the case of PINNs, a neural network is set up, where the physics is used as a constraint in the loss function, resulting in a black-box approach (Raissi et al., 2019 [7]). Generally, black-box approaches have the advantage of being easy to use. However, they have no guarantee of preserving the physics and yield “non-explainable” models (Willcox et al., 2021 [8]). Meaning, we do not know which “laws” the models follow. In application fields where physical knowledge is limited and data abundant this is a desired feature since the model can extract patterns from the provided data and develop its own “laws”, although retrieving these relationships is an open challenge. PINNs were designed for applications where data become sparser, meaning some physical knowledge is available as well as some data. Consequently, information from both data and physics is combined in the surrogate models. However, data in geodynamical applications can be extremely sparse, and, at the same time, are often needed to calibrate existing models. Hence, in these applications, it is desired to build on our physical knowledge instead of data. Naturally, data can be provided in form of simulation data but, in this case, black-box approaches have the above-mentioned disadvantages.
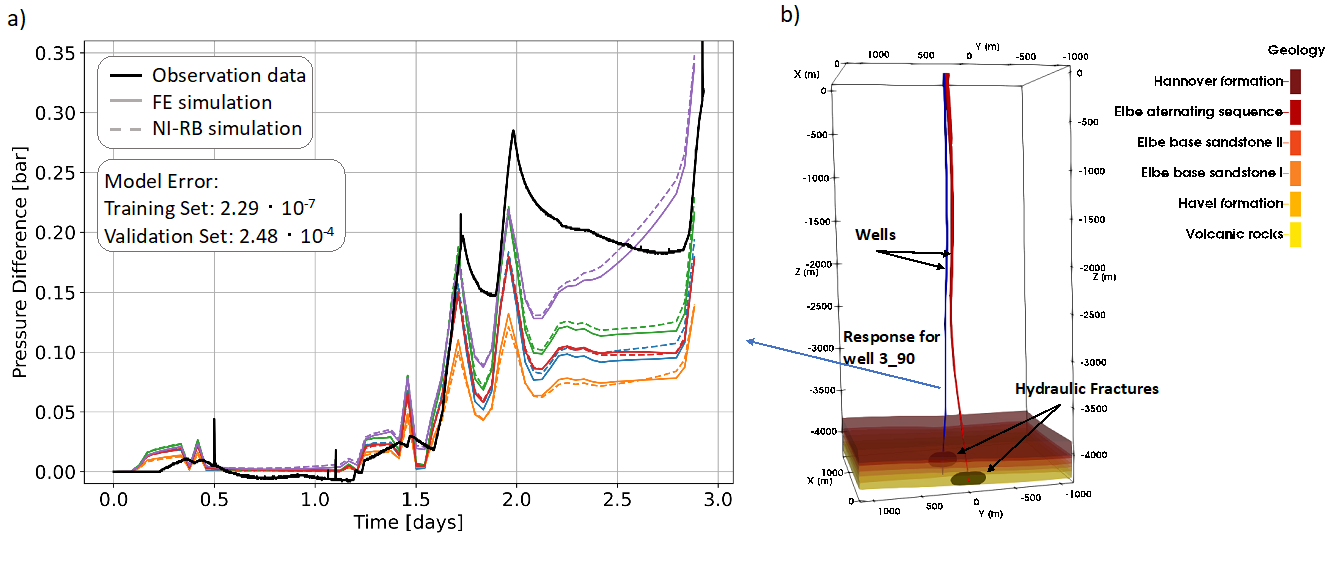
Figure 2: Example of a surrogate model constructed with the NI-RB method for a geothermal site in North-East Germany. In a) we illustrate the finite element solutions with solid colored lines, and the reduced solutions with colored dashed lines. The measurements are denoted with a black solid line. In b) the geological model is shown (Figure from Degen et al., 2022 [2]).
The Reduced Basis Method – Opportunities and Challenges
In contrast, the non-intrusive reduced basis method first extracts the characteristic of the physics and then uses the data-driven machine learning part to determine the weight of each of these characteristics (Degen et al., 2022 [2]; Hesthaven et al., 2018 [6]). The major difference to methods such as PINNs is that we obtain explainable models and that the non-rigorous part affects only the weighting. The resulting surrogate models are several orders of magnitude faster than the full-order models while maintaining the physical characteristic (Figure 2). This makes them very valuable in probabilistic uncertainty quantification and global sensitivity analysis, which both help us get a better understanding and assessment of subsurface processes. Such approaches also need considerably less amount of data. Previous studies showed very promising results for training data sets in the order of a hundred simulations. To achieve similar results with data-driven approaches, training data sets that are orders of magnitude larger would be required. This is an important point to keep in mind if considering the high computational cost of individual model solutions. Nonetheless, there is no such thing as a free lunch. Methods such as NI-RB allow for a higher control of the system but require more user interactions, especially in the data preparation phase (Degen et al., 2023 [3]). Furthermore, they face challenges for high-dimensional parameter spaces.
Coming back to the original question, is physics-based machine learning a curse or a blessing? If the right set of methods is chosen for the given application, it offers great potential since extensive investigations of the parameters that influence our models are possible. Nonetheless, if applied blindly it poses great risks since the answer will be misleading.
References: [1] van Zelst, I., Crameri, F., Pusok, A. E., Glerum, A., Dannberg, J., & Thieulot, C. (2021). 101 geodynamic modelling: How to design, carry out, and interpret numerical studies. Solid Earth Discussions, 2021, 1-80. https://doi.org/10.5194/se-13-583-2022 [2] Degen, D., Cacace, M., & Wellmann, F. (2022). 3D multi-physics uncertainty quantification using physics-based machine learning. Scientific Reports, 12(1), 17491. https://doi.org/10.1038/s41598-022-21739-7 [3] Degen, D., Caviedes Voullième, D., Buiter, S., Hendriks Franssen, H. J., Vereecken, H., González-Nicolás, A., & Wellmann, F. (2023). Perspectives of Physics-Based Machine Learning for Geoscientific Applications Governed by Partial Differential Equations. Geoscientific Model Development Discussions, 2023, 1-50. https://doi.org/10.5194/gmd-2022-309 [4] Benner, P., Gugercin, S., & Willcox, K. (2015). A survey of projection-based model reduction methods for parametric dynamical systems. SIAM review, 57(4), 483-531. https://doi/10.1137/130932715 [5] Hesthaven, J. S., Rozza, G., & Stamm, B. (2016). Certified reduced basis methods for parametrized partial differential equations (Vol. 590, pp. 1-131). Berlin: Springer. https://doi.org/10.1007/978-3-319-22470-1 [6] Hesthaven, J. S., & Ubbiali, S. (2018). Non-intrusive reduced order modeling of nonlinear problems using neural networks. Journal of Computational Physics, 363, 55-78. https://doi.org/10.1016/j.jcp.2018.02.037 [7] Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378, 686-707. https://doi.org/10.1016/j.jcp.2018.10.045 [8] Willcox, K. E., Ghattas, O., & Heimbach, P. (2021). The imperative of physics-based modeling and inverse theory in computational science. Nature Computational Science, 1(3), 166-168. https://doi.org/10.1038/s43588-021-00040-z