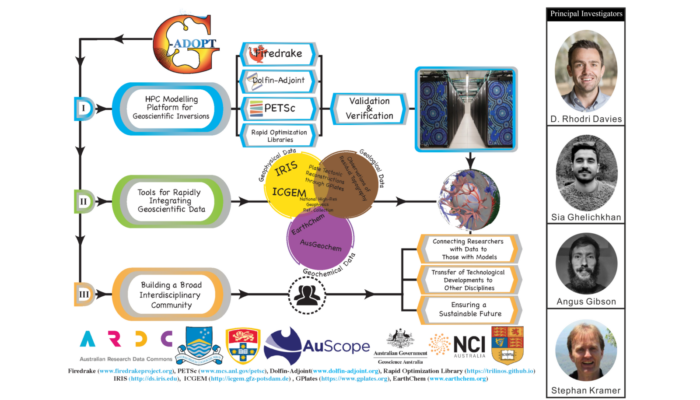
Schematic illustrating core components of G-ADOPT, an Australian based cross-NCRIS project, principally developed at the Australian National University (ANU), with partners at the University of Sydney and Imperial College London. G-ADOPT is supported by the Australian Research Data Commons (ARDC), with co-investment from AuScope, the National Computational Infrastructure (NCI) and Geosciences Australia.
The Geodynamic ADjoint Optimisation PlaTform (G-ADOPT) aims to develop and support a transformational new computational modelling framework for inverse geodynamics. It builds on several recent breakthroughs: (i) an ongoing surge in accessible observational datasets that constrain the structure, dynamics, and evolution of Earth’s mantle; (ii) advances in inversion methods, using sophisticated adjoint techniques, that provide a mechanism for fusing these observations with mantle models; and (iii) two novel software libraries, Firedrake and dolfin-adjoint, which when combined, provide a state-of-the-art finite element platform, with a fully-automated adjoint system, that offers a radical new approach for rigorously integrating geoscientific data (and uncertainties) with multi-resolution, time-dependent geodynamical models, through high-performance computing.
Motivating composable abstraction and automatic code generation
Since the advent of plate tectonic theory, there has been a long and successful history of research software development within the geodynamics community. The earliest modelling tools were restricted to a simplified approximation of the underlying physical system and, generally, to 2-D Cartesian geometries. However, in tandem with the ever increasing computational power of high-performance computing systems, rapid improvements in algorithmic design and software engineering, alongside the development of robust and flexible scientific computing libraries, have underpinned the development of more advanced research software infrastructure, which incorporate, for example, better approximations to the fundamental physical principles and offer increased flexibility. The user-base of these tools has rapidly increased, with development teams emerging to enhance their applicability and ensure their ongoing functionality. These teams have done so by adopting best-practices in modern software development, including version control, unit and regression testing across a range of platforms, and validation against a suite of analytical and benchmark solutions. This has been facilitated, in part, by the expansion of community driven efforts for software development, such as the Computational Infrastructure for Geodynamics (CIG) and the Simulation and Modelling (SAM) component of AuScope.
Even with these modern research software packages, some fundamental development decisions, such as the core physical equations, numerical approximations, and general solution strategy, have been integrated into the basic building blocks of the code. Whilst there remains some flexibility within the context of a single problem, modifications to include different approximations of the same physical system, for example, often require extensive and time-consuming development and testing, using either separate code forks or increasingly complex options systems. This makes reproducibility of a given simulation difficult, resulting in a lack of transparency. Those software frameworks that try to maintain some degree of flexibility often do so at the compromise of performance: the flexibility to configure different equations, numerical discretisations, and solver strategies, in different dimensions and geometries, requires implementation compromises in the choice of optimal algorithms and specific low-level optimisations for all possible configurations.
A challenge that remains central to research software development in geodynamics, therefore, is the need to provide accurate, efficient, flexible, easily extensible, scalable, transparent, and reproducible research software. However, this requires a large time commitment and knowledge that spans several disciplines. The consequence of this is that the development of research software for geodynamics has now become a multi-disciplinary effort and its design must enable scientists across several disciplines to collaborate effectively, without requiring each of them to comprehend all aspects of the system.
Key to achieving this is to abstract, automate, and compose the various processes involved in numerically solving the partial differential equations governing a specific problem, to enable a separation of concerns between developing a technique and using it. As such, software projects involving automatic code generation have become increasingly popular, as these help to separate different aspects of development. Such an approach facilitates collaboration between computational engineers with expertise in hardware and software, computer scientists and applied mathematicians with expertise in numerical algorithms, and domain specific scientists, such as geodynamicists.
This concept of composable abstraction underpins the G-ADOPT platform. G-ADOPT is built on the Firedrake project (e.g. Rathgeber et al. 2016) which, alongside the FEniCS project, has pioneered this approach for geoscientific computing. Firedrake is an automated system for solving partial differential equations using the finite element method, that is tailored towards geophysical fluid dynamics. It treats finite element problems as a composition of several abstract processes, using separate and open-source software components for each. Firedrake’s overarching goal is to save users from manually writing low-level code for assembling the systems of equations that discretise their model physics. It is written completely in Python and, through the use of domain specific languages, it allows the user to specify their problem at a high level of abstraction without having to worry about implementation details. The automatic code generation component of Firedrake translates this description into highly optimised low-level code, which incorporates detailed optimisations that are specifically targeted at the configuration of the problem that is being solved. This facilitates levels of optimisation that would be impossible or impractical to achieve in a general purpose model directly written in lower level programming languages.
Firedrake therefore creates a separation of concerns between employing the finite element method and implementing it. This is a game-changer: it opens finite element problems to a new class of user and developer.
In a recent paper (Davies et al. 2022), published as part of a Firedrake special issue at Geoscientific Model Development following 7 (!) constructive reviews, we demonstrate the applicability of Firedrake for geodynamical simulation, with a focus on mantle dynamics. We present, analyse, and validate Firedrake against well-known benchmark and analytical cases of systematically increasing complexity, building towards a global, time-dependent compressible simulation with complex (non-linear) rheology, forced by 230 Myr of surface plate tectonic histories. Figure 1 illustrates the present-day thermal structure predicted by this simulation, which displays many characteristics compatible with seismic images of Earth’s mantle.
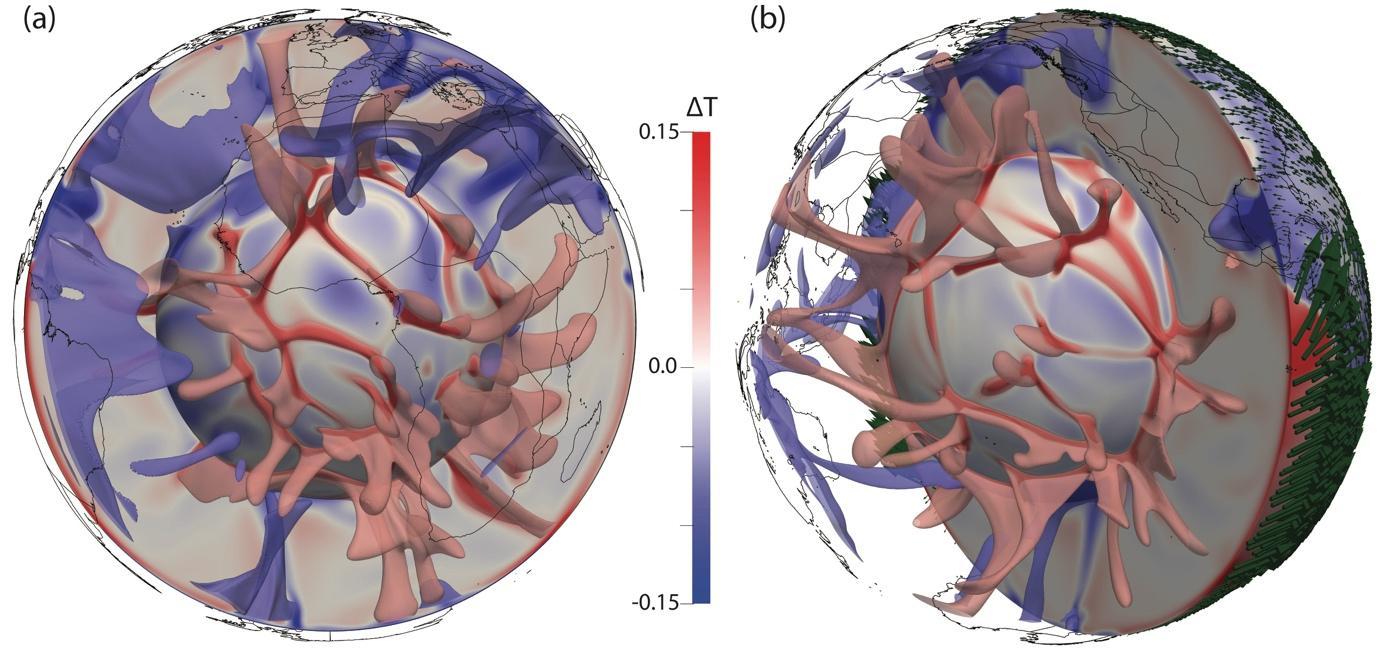Figure 1: Present-day thermal structure, predicted from a global mantle convection simulation in Firedrake where the geographic distribution of heterogeneity is dictated by 230 Myr of imposed plate motion history (from Muller et al. 2016). Each image includes a radial surface immediately above the core-mantle boundary, a cross-section, and transparent isosurfaces at temperature anomalies (i.e. away from the radial average) of T=-0.075 (blue) and T=0.075 (red), highlighting the location of downwelling slabs and upwelling mantle plumes, respectively. Continental boundaries provide geographic reference. Panel a provides an Africa-centered view, with panel b centered on the Pacific Ocean, and including (green) glyphs at the surface highlighting the imposed plate velocities.
The elegance of Firedrake is best highlighted through a simple example: isoviscous, incompressible convection, in an enclosed 2-D box (reproducing a case better known within the community as the Blankenbach benchmark). Solutions are obtained by solving the Stokes equations for velocity and pressure, alongside the energy equation for temperature, using a standard time-splitting algorithm. The Firedrake code for this is included in Figure 2. The finite element method is well-suited to automatic code-generation techniques: a mesh (constructed on line 5 utilising Firedrake’s built-in meshing functionality), appropriate discrete function spaces (lines 11-22), a weak formulation of the governing PDEs (specified using the Unified Form Language, which closely mimics the mathematical formulation, on lines 34-38), together with initial conditions (lines 25-27), boundary conditions (lines 41-42), solver and problem configurations (lines 51-62), is sufficient to fully represent the core components of this case. Indeed, in only 56 lines of Python (excluding comments and blank lines), Firedrake can reproduce the benchmark results. Moreover, the changes required to run more realistic problems are minimal, as is clearly documented in the paper, where we progress systematically from this simple 2-D case towards the global 3-D spherical simulation illustrated in Figure 1.
Figure 2: Firedrake code required to reproduce 2-D Cartesian incompressible isoviscous benchmark cases from Blankenbach et al. (1989).
Firedrake has allowed us to deliver on the first goal of the G-ADOPT platform: to support a transformation in the speed at which geodynamical research can be undertaken. It provides a means to rapidly generate accurate, efficient, flexible, easily extensible, scalable, transparent, and reproducible research software infrastructure.
It looks like a great platform for geodynamics, but what about the adjoint?
Mantle convection is a time-dependent process, as evidenced by the large-scale plate reorganisations in plate tectonic reconstructions of the lithosphere: the mantle’s upper thermal boundary layer. While detailed kinematic reconstructions of past plate-motions have been developed, they are not matched by equivalent knowledge of the thermo-chemical structure and flow history in the underlying mantle. This is a major limitation, as it inhibits our ability to understand fundamental processes that depend on time-dependent interactions between Earth’s surface and its deep interior.
The difficulty of inferring mantle flow into the past principally occurs because mantle convection is uniquely determined by an initial condition sometime in the past (alongside boundary conditions at the surface and core-mantle-boundary). Because this initial condition is unknown, we cannot tightly constrain the evolution of mantle flow from forward mantle convection calculations. This obstacle can be overcome by reformulating global mantle flow simulations as an inverse problem, through large-scale iterative optimisation.
Such an approach finds an optimal initial condition by minimising a misfit function that measures the difference between model predictions and inferences on mantle structure obtained from observational datasets. This can be achieved by employing the derivative of a mantle convection model relative to an earlier flow structure, through the so-called adjoint method: it allows us to reconstruct the mantle’s thermo-chemical structure and evolution with respect to available observations (see, for example, Bunge et al. 2003; Liu et al. 2008; Ghelichkhan et al. 2021).
Adjoints, more generally, are key ingredients in many important algorithms, such as data assimilation, optimal control, sensitivity analysis, design optimisation and error estimation. They have had an enormous impact in fields such as meteorology and oceanography. However, their use in other scientific fields, including geodynamics, has been hampered by the great practical difficulty of their derivation and implementation, alongside their extreme computational cost.
G-ADOPT aims to overcome the practical challenge of developing and implementing adjoints, using a higher-level abstraction for developing discrete adjoint models (see Farrell et al. 2013). This functionality is provided through dolfin-adjoint, in a form that is fully compatible with Firedrake. The combination of Firedrake and dolfin-adjoint, therefore, provides a state-of-the-art finite element platform, with fully automated adjoint solutions, offering a radical new approach for rigorously integrating geoscientific data (and uncertainties) with multi-resolution, time-dependent, geodynamical models, through high-performance computing.
We are in the process of validating this approach for global simulations with Earth-like physical approximations and observational datasets. Once complete, we will deliver on the second major goal of the G-ADOPT project: to support a transformation in the type of research that can be undertaken by the community, by providing a means to move from idealised forward models to data-driven simulations that rigorously account for observational constraints and their uncertainties.
Timeline and Community Building
We are 18 months into this exciting project. At present, we are extending the series of geodynamical examples presented in our paper, to facilitate multi-material simulations, which are used extensively by the geodynamical modelling community. Concurrently, we are exploring the use of new iterative solution strategies for the Stokes system, to improve computational efficiency: a major benefit of Firedrake is access to the wide variety of solution algorithms and preconditioning strategies provided by the PETSc library, which can be flexibly configured through a solver parameters dictionary, allowing one to test and apply different strategies with ease.
The focus of current development, however, is the validation, verification and optimisation of adjoint models, under different physical approximations. Early results are promising and will be coming to a journal near you soon!
Our flexible design ensures that any technological developments can be rapidly and directly transferred to other fields. Indeed, we have begun to apply the G-ADOPT framework within new geoscientific areas, including simulating: (i) the response of Earth’s surface and global sea level to melting polar ice sheets (within the Australian Centre of Excellence for Antarctic Science); and (ii) seismic wave propagation. In that sense, the project has already achieved its goal of increasing the rate at which knowledge and tools can be developed, executed and transferred to other fields.
We note that the G-ADOPT platform is being developed in full compliance with FAIR (Findable, Accessible, Interoperable, Reusable) principles. All examples presented in our GMD paper are archived. Firedrake integrates with Zenodo and GitHub to provide users with the ability to generate a set of DOIs corresponding to the exact set of Firedrake components used to conduct a particular set of simulations. By providing our input scripts and a DOI for the version of Firedrake used in the paper, we ensure traceable provenance of model data. Continuous Integration testing ensures that the setups also continue to work with the latest version of the entire software stack.
Community building is a core aim of our platform: we would like to see the community of developers and users broaden as the program evolves. To enable training, support, and community-driven development, we hold annual workshops for all project participants and interested practitioners. In 2022, we held a workshop focussed on Firedrake and the forward modelling component of our platform at the ANU. A series of tutorials are available from this workshop to support new users (executable in Google Colab). In mid-2023, we plan to hold a second workshop that will focus on: (i) the development and application of adjoint models; and (ii) identifying the needs of our broader community.
To be kept updated on our progress, plans and workshops, please sign up to our mailing list, accessible through our website (at the base of our homepage).
* Special thanks to Sia Ghelichkhan, Stephan Kramer and Angus Gibson, who also contributed to the writing and proof-reading of this blog.
Blankenbach, B., Busse, F., Christensen, U., Cserepes, L., Gunkel, D., Hansen, U., Harder, H., Jarvis, G., Koch, M., Marquart, G., Moore, D., Olson, P., Schmeling, H., Schnaubelt, T., 1989. A benchmark comparison for mantle convection codes. Geophys. J. Int. 98, 23–38. https://doi.org/10.1111/j.1365-246X.1989.tb05511.x Bunge, H.-P., Hagelberg, C.R., Travis, B.J., 2003. Mantle circulation models with variational data assimilation: inferring past mantle flow and structure from plate motion histories and seismic tomography. Geophys. J. Int. 152, 280–301. https://doi.org/10.1046/j.1365-246X.2003.01823.x Davies, D.R., Kramer, S.C., Ghelichkhan, S., Gibson, A., 2022. Towards automatic finite-element methods for geodynamics via Firedrake. Geosci. Model Dev. 15, 5127–5166. https://doi.org/10.5194/gmd-15-5127-2022 Farrell, P.E., Ham, D.A., Funke, S.W., Rognes, M.E., 2013. Automated Derivation of the Adjoint of High-Level Transient Finite Element Programs. SIAM J. Sci. Comput. 35, C369–C393. https://doi.org/10.1137/120873558 Ghelichkhan, S., Bunge, H.-P., Oeser, J., 2021. Global mantle flow retrodictions for the early Cenozoic using an adjoint method: evolving dynamic topographies, deep mantle structures, flow trajectories and sublithospheric stresses. Geophys. J. Int. 226, 1432–1460. https://doi.org/10.1093/gji/ggab108 Liu, L., Spasojević, S., Gurnis, M., 2008. Reconstructing Farallon Plate Subduction Beneath North America Back to the Late Cretaceous. Science, 322(5903), 934-938. https://doi.org/10.1126/science.1162921 Müller, R.D., Seton, M., Zahirovic, S., Williams, S.E., Matthews, K.J., Wright, N.M., Shephard, G.E., Maloney, K.T., Barnett-Moore, N., Hosseinpour, M., Bower, D.J., Cannon, J., 2016. Ocean Basin Evolution and Global-Scale Plate Reorganization Events Since Pangea Breakup. Annu. Rev. Earth Planet. Sci. 44, 107–138. https://doi.org/10.1146/annurev-earth-060115-012211 Rathgeber, F., Ham, D.A., Mitchell, L., Lange, M., Luporini, F., Mcrae, A.T.T., Bercea, G.-T., Markall, G.R., Kelly, P.H.J., 2016. Firedrake: automating the finite element method by composing abstractions. ACM Trans. Math. Softw. 43, 1–27. https://doi.org/10.1145/2998441
