
This week Daniel Douglas, who is now a PhD student at New Mexico Tech, discusses his master thesis research while at the university of Hawaii. He investigated the role of magma in the flexure of the Hawaiian lithosphere.

Daniel is currently a PhD student at New Mexico Tech. His research consists of running geodynamic models of dehydration reactions in subduction zones.
When a topographic load is applied to the lithosphere, the lithosphere accommodates the load by flexing. The observed flexure can be measured through seismic methods, gravity anomalies, and satellite altimetry (Cazenave 1980, Watts et al, 1985). The characteristic shape of lithospheric flexure, shown and exaggerated in the schematic diagram below, is controlled by the shape and weight of the load, as well as the strength of the lithosphere.
If the shape of the flexed surface of the lithosphere is known, and the shape and weight of the load is known, then geodynamic calculations of load-induced lithosphere deformation can be performed to gain insight into the processes controlling that deformation. This has been done for a multitude of geologic settings like the Azores Plateau, various Pacific seamounts, and from postglacial rebound of the Laurentide ice sheet (Peltier 1976, Burov & Diament 1995, Luis & Neves 2006) and models that relate observations of flexure to the physical properties of the lithosphere have become increasingly sophisticated. Early studies used theory for thin elastic plates typically constrained by gravity measurements of the flexed lithosphere in response to topographic loads to characterize an effective elastic plate thickness, which can be related to lithosphere strength through the flexural rigidity. (Walcott 1970). However, this represents a static rheologic response that is solely elastic (Burov & Diament 1995).
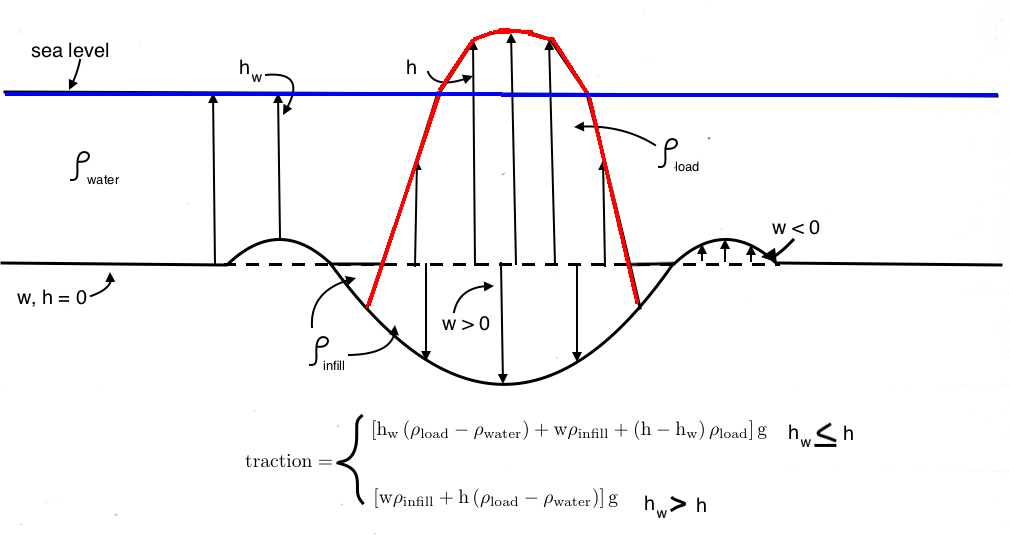
Schematic diagram showing how an island load (outlined in red) deforms the lithosphere (black surface) The amount of flexure (w) depends on load shape (h) and load density, as well as the strength of the lithosphere beneath the load.
Observations of deformation that occur before the load is fully compensated by the lithosphere are well explained by models of thin elastic plates overlying a viscous medium, indicating a coupling of elastic and viscous (viscoelastic) deformation. However, more modern modelling efforts have moved away from thin-plate approximations and calculate load-induced deformation of the upper mantle using equations that describe more realistic rheologies based on rock physics experiments, including brittle deformation, low-temperature creep, and high-temperature creep. Unlike brittle deformation and high-temperature creep, low-temperature creep is a deformation regime that remains poorly understood. Several independent laboratory experiments seeking to constrain the low-temperature regime have yielded a wide range of values in the parameters controlling low-temperature creep. Studies like (Zhong & Watts 2013, Bellas et al, 2020) sought to constrain low-temperature creep by modeling flexure beneath the Hawaiian Islands and used seismic imagery of the top of the flexed oceanic crust to constrain their model results. They found that all low-temperature creep flow laws derived from laboratory experiments were too strong to reproduce the flexure observed in the seismic data. However, they did not consider the effect that localized magmatic weakening would have on lithospheric strength.
In tandem with new seismic data imaging the top of the oceanic crust parallel and perpendicular to the Hawaiian Island chain, I used the open source CIG supported modeling code ASPECT (see Kronbichler et al., 2012; Heister et al., 2017; Bangerth et al., 2021b,a; Rose et al.,2017; Fraters et al., 2019) to try to test the effect that magmatic heating would have on the lithospheric response to the massive top-down load of the Hawaiian Islands. The effect that heating the lithosphere would have can easily be predicted by looking at the rheological equation for low-temperature creep:
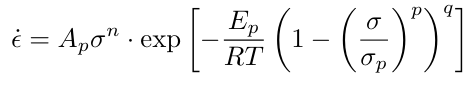
Rheological expression for low-temperature creep relating strain rate έ to stress σ. Important relationship is temperature T in the inverse of the exponent.
Though this is an intimidating expression at first glance, the key thing to note is that the strain rate is proportional to the temperature in the inverse of the exponent. This means that, all other things equal, the hotter the material is the weaker it will behave. The question that needs to be answered is how much weaker will it behave, and will this thermal weakening alone overcome the results of previous studies that lab experiments propose low-temperature flow laws that are too strong to model Hawaiian lithosphere. There are good reasons to assume that the Hawaiian lithosphere is anomalously hotter than ambient lithosphere of the same age. Xenolith samples erupted from Salt Lake Crater on Oʻahu indicate that they were formed at temperatures ~200-300 degrees hotter at depths of 40-60 km than the expected geotherm calculated using a plate cooling model (Guest et al. 2020). S-wave speeds that are up to 4% slower than expected are also indicative of a hotter lithosphere at depths of 40km beneath the islands (Laske et al 2011, Cheng et al 2015).
One of the key components to tackling a problem like this is simulating a realistic rheology, which thankfully is something that ASPECT is fully equipped to deal with. A composite visco-elastic-plastic rheological model is built into the source code of ASPECT and allows for an inclusion of a wide range of deformation regimes. In this case, regimes included are brittle deformation simulated by a Drucker-Pragar yield criterion, elastic deformation, low-temperature Peierls creep, and high-temperature dislocation creep.
A second key component of modeling this unique geologic setting was to capture the growth of the Hawaiian Islands through time as hot spot volcanism accreted magma to the surface. As the island chain spanning from Niʻihau to Hawaiʻi grew over the past 6 Million years, so did the traction applied to the Pacific lithosphere. Since the new seismic data used to constrain flexure calculations is a snapshot of the deformation at present day, and since this type of deformation does not occur instantaneously, a first order model for growing the islands in ASPECT was crucial. Using age estimates of main shield phase volcanism for 13 volcanic centers and gaussian growth functions, the animation below shows the first order model used to grow the load of the Hawaiian Islands.

Animation showing the growth of the Hawaiian Islands from Niʻihau (top right) to Hawaiʻi (bottom left) over 6 Myr.
The last key component was the initial thermal structure and simulating how magma heats the lithosphere at shallow to intermediate depths. For the initial thermal structure the seafloor age model of Mueller et al. 2016 was used to generate geotherms using the plate cooling model of Parson’s & Sclater 1977. For simulating magmatic heating, a method known as ‘thermal rejuvenation’ was chosen. Thermal rejuvenation takes the age of the lithosphere used to prescribe a geotherm in a plate cooling model, and effectively reduces the ‘age’ to produce a warmer geotherm. In this second animation oceanic lithosphere with an age of 90 Myr is thermally rejuvenated to an age of 40 Myr, effectively heating the lithosphere and causing it to behave weaker under an applied load. This method for heating the lithosphere is coupled with the previously described growth model in order to simulate how the magma heats up the lithosphere as it intrudes upward and erupts on the surface, growing the island chain.
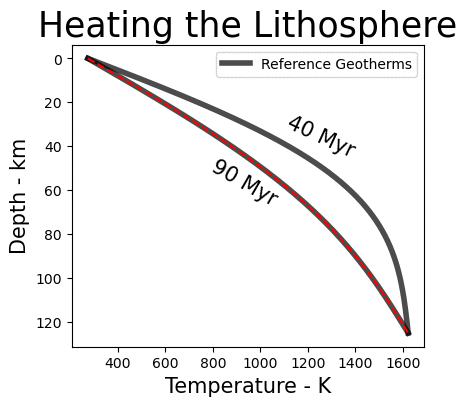
Gradual thermal rejuvenation of a 90 Myr oceanic lithosphere geotherm to a 40 Myr geotherm.
The combination of these three key components results in complex calculations of flexure in a realistic visco-elastic-plastic lithosphere subject to a temporally varying coupled loading and heating model. Keep your eyes peeled for an in depth discussion of the results of these models in a (hopefully) soon to be published paper!
References: Bangerth, W., Dannberg, J., Fraters, M., Gassmoöeller, R., Glerum, A., Heister, T., & Naliboff, J. (2021a, July). ASPECT: Advanced Solver for Problems in Earth’s ConvecTion, User Manual Bangerth, W., Dannberg, J., Fraters, M., Gassmoöeller, R., Glerum, A., Heister, T., & Naliboff, J. (2021b, July). Aspect v2.3.0. Zenodo Bellas, A., Zhong, S., & Watts, A. (2020, 01). Constraints on the rheology of the lithosphere from flexure of the Pacific plate at the Hawaiian Islands. Geochemistry, Geophysics, Geosystems, 21 Burov, E., & Diament, M. (1995). The effective elastic thickness (Te) of continental lithosphere: What does it really mean? Journal of Geophysical Research, 100, 3905-3927 Cazenave, A., Lago, B., Dominh, K., & Lambeck, K. (1980). On the response of the ocean lithosphere to seamount loads from geos 3 satellite radar altimeter observations.Geophysical Journal International, 63, 233-252. Cheng, C., Allen, R. M., Porritt, R. W., & Ballmer, M. D. (2015). Seismic constraints on a double-layered asymmetric whole-mantle plume beneath Hawaii. Hawaiian Volcanoes: From Source to Surface, Geophysical Monographs, 208, 19-34 Fraters, M. R. T., Bangerth, W., Thieulot, C., Glerum, A. C., & Spakman, W. (2019, 04). Efficient and practical Newton solvers for nonlinear Stokes systems in geodynamics problems. Geophysics Journal International, 218(2), 873-894. Guest, I., Ito, G., Garcia, M., & Hellebrand, E. (2020, 11). Extensive magmatic heating of the lithosphere beneath the Hawaiian Islands inferred from Salt Lake Crater mantle xenoliths. Geochemistry, Geophysics, Geosystems, 21 Heister, T., Dannberg, J., Gassmöller, R., & Bangerth, W. (2017). High accuracy mantle convection simulation through modern numerical methods. II: Realistic models and problems. Geophysical Journal International, 210(2), 833-851. Kronbichler, M., Heister, T., & Bangerth, W. (2012). High accuracy mantle convection simulation through modern numerical methods. Geophysical Journal International, 191, 12-29 Laske, G., Markee, A., Orcutt, J., Wolfe, C., Collins, J., Solomon, S., . . . Hauri, E. (2011,12). Asymmetric shallow mantle structure beneath the Hawaiian Swell—evidence from Rayleigh waves recorded by the PLUME network. Geophys. J. Int, 187, 1725-1742 Luis, J., & Neves, M. (2006, 04). The isostatic compensation of the Azores Plateau: A 3D admittance and coherence analysis. Journal of Volcanology and Geothermal Research, 156, 10-22. Müller, D., Seton, M., Zahirovic, S., Williams, S., Matthews, K., Wright, N., . . . Cannon, J. (2016, 06). Ocean basin evolution and global-scale plate reorganization events since Pangea breakup. Annual Review of Earth and Planetary Sciences, 44, 107-138. Parsons, B., & Sclater, J. G. (1977). An analysis of the variation of ocean floor bathymetry and heat flow with age. Journal of Geophysical Research, 82(5), 803-827 Peltier, W. R., & Andrews, J. T. (1977). Glacial-isostatic adjustment-I. the forward problem. Geophysical Journal International, 46, 605-646 Rose, I., Buffett, B., & Heister, T. (2017). Stability and accuracy of free surface time integration in viscous flows. Physics of the Earth and Planetary Interiors, 262, 90 -100 Walcott, R. I. (1970). Flexural rigidity, thickness, and viscosity of the lithosphere. Journal of Geophysical Research, 75, 3941-3954 Watts, A., Buhl, P., & Brocher, T. (1985, 05). A multichannel seismic study of lithospheric flexure across the Hawaiian-Emperor seamount chain. Nature, 315 Zhong, S., & Watts, A. B. (2013). Lithospheric deformation induced by loading of the Hawaiian Islands and its implications for mantle rheology .Journal of Geophysical Research: Solid Earth, 118, 6025-6048
