This week UCLA PhD student Leslie Insixiengmay takes us on a microscopic journey to the Earth’s interior and tells us all about the atomic forces that shape the deep Earth behaviour!
A question I get asked a lot is: “How do we know what’s inside of the Earth?” It’s a good and valid question considering that the deepest hole humans have dug only reaches about 12.2 km, which is about 0.2% of the Earth itself (Kozlovsky, 1984). So how is it that scientists can boldly claim to know what’s inside of the Earth without ever having seen the interior? The answer is complex, but it can boil down to the combination of astronomical, chemical constraints, seismology, and mineral physics.
Mineral physics is a discipline that involves understanding materials in planetary interiors while trying to fit the observed chemical and seismological constraints. The composition of the Earth cannot be very different from that of the Sun or meteorites, thus providing a chemical constraint on the building blocks of Earth (McDonough and Sun, 1995). Additionally, we have another constraint provided by seismic observations. Every time an earthquake occurs, seismic waves propagate through the Earth and we gain insight as to what the inside of the Earth looks like. This technique is called “seismic tomography,” which is very similar to receiving a medical X-ray computed tomography scan, or better known as a CT scan. You can compare imaging the interior of the Earth using seismic waves to imaging the insides of human bodies using X-ray CT scans. Different mineral assemblages and phases within Earth’s interior produce different seismic wave velocity profiles that can be imaged.
Like many other STEM disciplines, mineral physics has both an experimental and theoretical side. The experimental side involves laboratory work, where minerals are squeezed and heated to high pressures and temperatures– mimicking the conditions of a planetary interior – so that we can understand how materials behave at such extreme conditions. The theoretical side, which I will be focusing on from here on out, involves using computer models of minerals and materials at these extreme conditions. But before we talk about how minerals can be simulated, we first must understand what a mineral is.
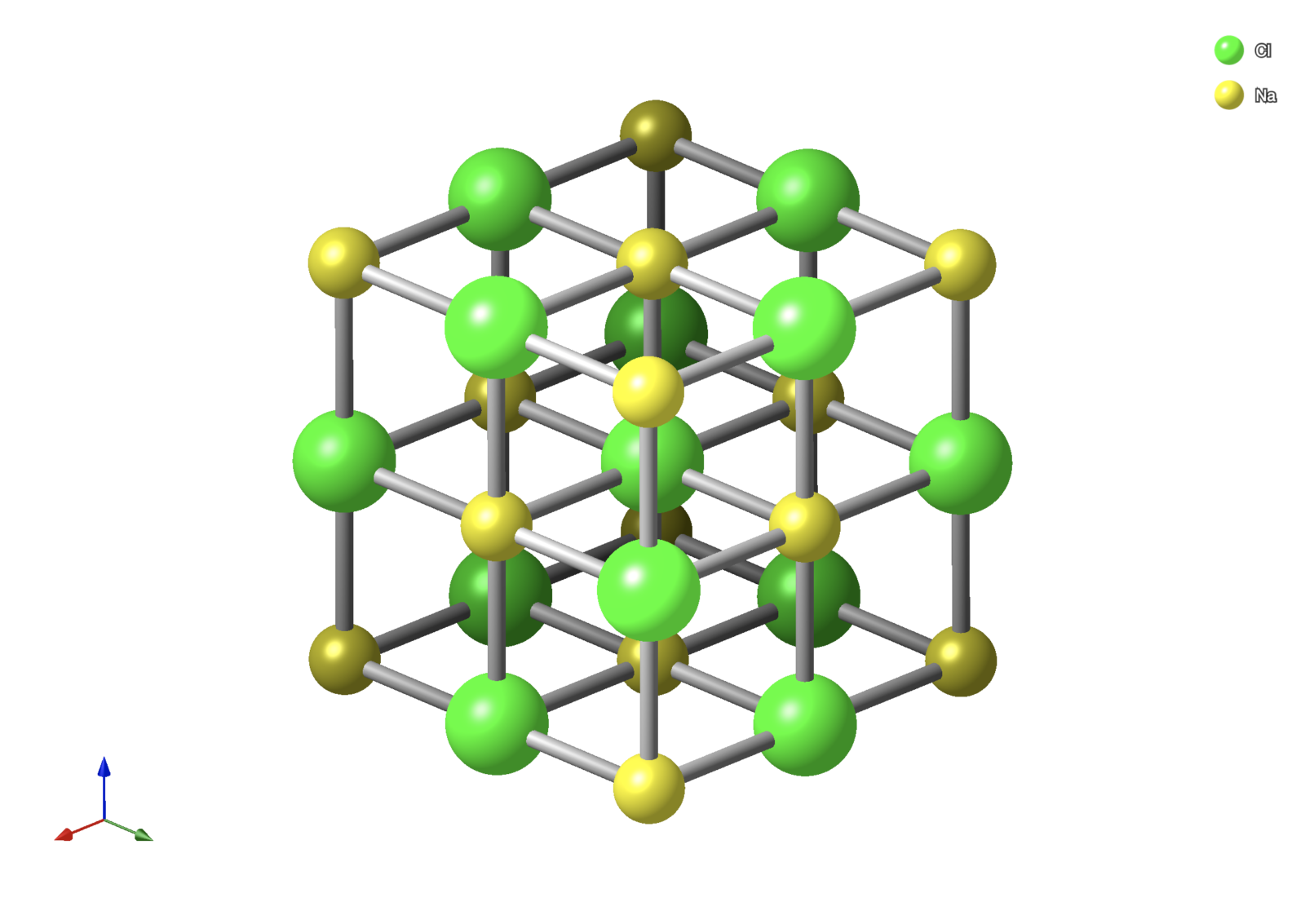
Figure 1: Atomic structure of halite, NaCl, generated from CrystalMaker.
A mineral is defined as naturally occurring, inorganic, solid, having a well-defined crystalline structure, and having a well-defined chemical composition (Nickel, 1995; Nickel and Grice, 1998). Here, I’ll be emphasising the chemical composition aspect of a mineral, or in other words the arrangement of atoms that make up the mineral. For example, rock salt is a mineral called “halite,” and its chemical composition is comprised of two atom types called sodium and chlorine, or together can be abbreviated by NaCl. So, you can think of atoms as the building blocks of minerals. This property is important because it allows scientists to treat atoms as a mathematical problem.
Mathematically, we can incorporate Newton’s laws of motion to simulate an atom’s trajectory by treating it as if it is a classical object, or an object that we can see with the naked eye. The same laws that govern the trajectory of a cannonball are used to predict atomic motion. In a nutshell, this means that if you poke an object, which has some mass, that object will move. If you poke it harder, it’ll move faster. Here, the poking is equivalent to the force and the movement is equivalent to the acceleration. If we poke an atom with enough force, it should move! Very simple, right? This is the basis of a technique called Molecular Dynamics (MD), which predict how atoms will move with time with a given force. Of course, we can get a lot more sophisticated than this, and we still have some overarching questions that still have not been addressed: 1.) How do we know how much force to poke an atom with, and how do you map atomic movement over time? 2.) How does this mimic the Earth’s interior?
How much force do we use?
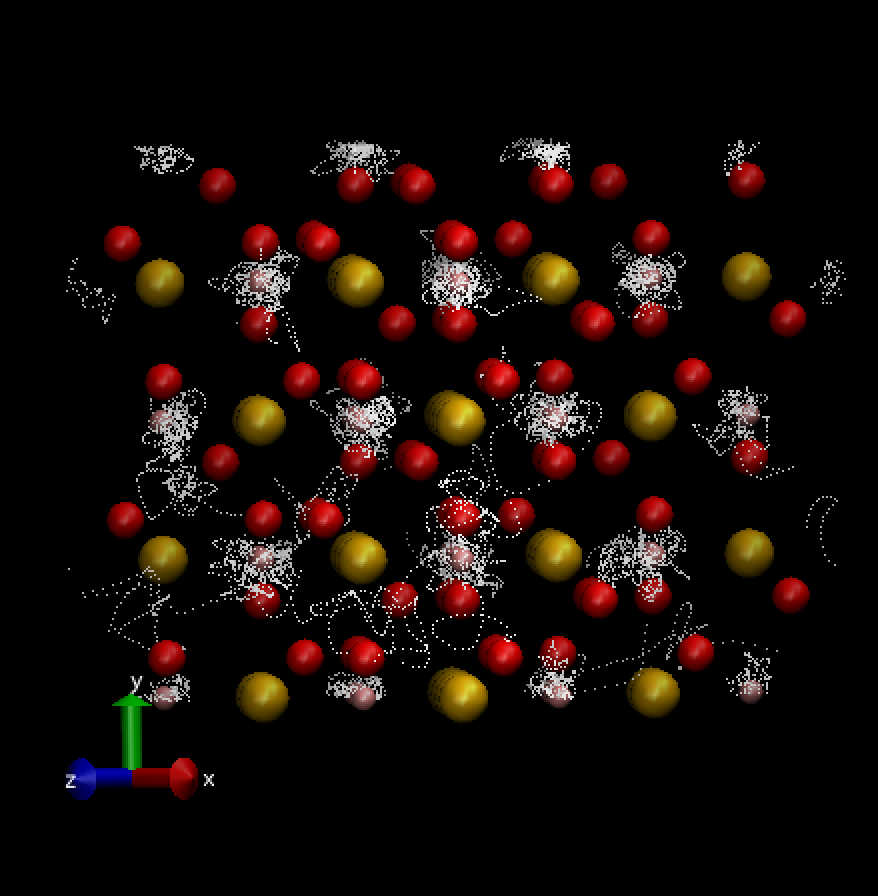
Figure 2: A simulation performed on pyrite-FeO2H showing the trajectory of hydrogen atoms in white dashed lines. Atoms are represented as spheres with iron in gold, oxygen in red, and hydrogen in pink.
How do we know how much force to poke an atom with? Addressing this question involves the combination of MD simulations and a method called Density Functional Theory (DFT). Physically, atoms do not usually behave classically but instead behave quantum mechanically, or at a microscopic level where the positions and momentum are uncertain. DFT is a computational quantum mechanical modelling method that approximates the electronic structures and interactions of a many-body system, allowing us to calculate the total energy and forces for any given snapshot of nuclear positions (Kohn et al. 1996; Kohn 1999). In other words, a method that is very useful for computing total energies of atoms that have more than one electron (which is nearly every element found in Earth materials). The forces can be calculated by taking the derivative of the total energy. This quantum mechanical result is utilised for the MD simulations where the motion of atoms is treated classically and incorporate Newton’s laws of motion, and the trajectory of atoms within a mineral can be simulated over some given time frame (usually on a femtosecond scale, or 10-15 seconds!). The combination of MD and DFT allows us to observe atomic-level changes and to calculate the forces and stresses for ionic motion.
How do simulations mimic the Earth’s interior?
Recall that minerals are treated as arrangements of atoms. MD calculations treat the atoms as independent particles, but we can take a step back and think of treating the entire collection of atoms as an ensemble. This is due to the computational limitations of modern-day computers and the number of atoms that we can simulate in a calculation. For example, one gram of NaCl is on the order of 1025 atoms, which would be impossible to calculate within our lifetimes when scaling this to the Earth. To get around this problem, we treat atomic systems by incorporating statistical mechanics: a physics discipline that uses a mathematical framework to apply statistics and probability theory to large amounts of microscopic ensembles. A major goal of statistical mechanics is to derive classical thermodynamic properties of materials in terms of the particles and the interactions between them. From our simulations, we can calculate equilibrium energies of systems at a given temperature and pressure condition. With these energies, we can calculate thermodynamic properties and predict stable mineral assemblages and phases. Thermodynamic properties of materials can also be measured experimentally, giving us a constraint between observations and theory.
Tying everything together
The advancement in seismological tomography and mineral physics has led to the development of models that can relate seismic observations to material properties (Stixrude and Lithgow-Betelloni, 2005). One such example is the prediction and observation of mineral phases such as the transition of perovskite to post-perovskite (Murakami et al., 2004) both in the lab and at the Earth’s lower most mantle. The thermodynamic and physical properties calculated from theory and measured from experiments can be compared to the information we gain from seismic wave observations such as pressure, density, and elastic moduli as a function of depth (Bullen and Bolt, 1985). The agreement between observation and theory is a confirmation that the methods described above work well and give us better insight as to what the Earth’s interior looks like!
References Bullen, Keith Edward, and Bolt, Bruce, A. "An introduction to the theory of seismology". Cambridge university press, 1985. Kohn, Walter, Axel D. Becke, and Robert G. Parr. "Density functional theory of electronic structure." The Journal of Physical Chemistry 100.31 (1996): 12974-12980. Kohn, Walter. "Nobel Lecture: Electronic structure of matter—wave functions and density functionals." Reviews of Modern Physics 71.5 (1999): 1253. Kozlovsky, Ye A. "The world's deepest well." Scientific American 251.6 (1984): 98-105. McDonough, William F., and S-S. Sun. "The composition of the Earth." Chemical geology 120.3-4 (1995): 223-253. Murakami, Motohiko, et al. "Post-perovskite phase transition in MgSiO3." Science 304.5672 (2004): 855-858. Nickel, Ernest H. "Definition of a mineral." Mineralogical Magazine 59.397 (1995): 767-768. Nickel, Ernest H., and Joel D. Grice. "The IMA Commission on New Minerals and Mineral Names: procedures and guidelines on mineral nomenclature, 1998." Mineralogy and Petrology 64.1 (1998): 237-263. Stixrude, Lars, and Carolina Lithgow-Bertelloni. "Thermodynamics of mantle minerals—I. Physical properties." Geophysical Journal International 162.2 (2005): 610-632.
