Simplified models or toy models explain the complex Earth processes fairly well, even though they are far from reality. In this week’s Geodynamics 101, Adam Beall, Research Associate at Cardiff University, discusses some of his favourite geophysical toy models!
I remember being excited to first hear about scientists doing Earth modelling and imagined impressive computer visualisations of tectonic plates crashing and reconstructions of complex geological maps. Instead, I found myself in a geodynamics class playing with a lava lamp. I have since used calculations that modelled mountains as floating blocks and read about shear-zones modelled with lentils. Not quite what I initially expected from the frontiers of science!
It turns out that these simplifications of the complex world around us are intentional and beneficial. There are many physical processes going on in the Earth and many equations needed to model them, along with many different rock properties. To make a model that can be reproduced mathematically or in the lab, we need to choose key equations and make educated assumptions about rock properties. Supercomputers can now be used to solve complex equations, but often give an answer for specific rock property choices and it can be difficult to understand the answer we get. The most simplified models can often be solved with pen and paper for any rock property choice and can be thoroughly understood, bringing generalised insights.
Simplified models are often called ‘toy models’, where the ‘toy’ label highlights the idea of being able to ‘pull apart’ and ‘play’ with a simple model and potentially even build physical replicas. I would like to share some of my favourite toy models with you, which are surprisingly relevant to the Earth despite their simplicity.
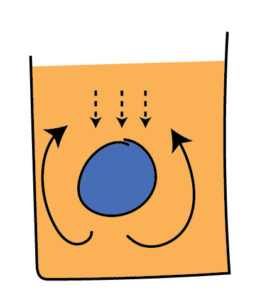
Stokes Sinker
Fill a glass of honey and drop a spherical glass marble in – it will take a little while to sink to the bottom (as in this video) and drive circulation of the honey. This can be modelled by an exact solution to the Navier-Stokes equations, which is called Stoke’s law or Stoke’s settling velocity. The mathematical model reveals how the velocity of the sinking sphere depends on its buoyancy, size and the viscosity of the fluid. It turns out that Stokes’ law gives a reasonable estimate of how quickly slabs sink and explains why old sea-floor subducts more quickly. It also predicts how quickly plumes rise or how crystals settle through magma or sediment through water.
Convection
Put on the kettle for a cup of tea – the element heats up the water only at the base of the kettle, but somehow all of the water heats up very quickly. This is because hot fluids expand and become buoyant, while cold fluids contract and become dense, driving circulation up and down. This process is complex, but it is possible to mathematically model whether the hot and cold layers start to mix together or if they remain stationary. This would appear to depend on many parameters (density, viscosity, thermal expansivity, etc.), but can be mathematically reduced to depending on a single parameter called the Rayleigh number. The Rayleigh number captures the relative rates of thermal diffusion and fluid flow and a critical value predicts the onset of mixing. This calculation can be used to explain heat-loss from the ocean floor and why Earth has plate tectonics. Despite the rigidity of the Earth’s cold surface, the mantle convects in an analogous way to a kettle or lava lamp.
Spring-block Slider
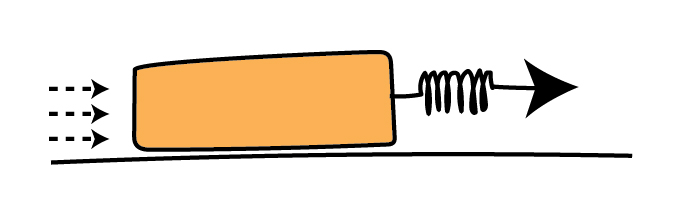Put a heavy block on some sandpaper, attach a spring to its side and pull the spring until the block slides. The block will start sliding suddenly and abruptly stop, in a motion that mimics earthquakes. The mathematical model of this spring-block slider captures how energy is loaded elastically by tectonic motion and then released during an earthquake. It reveals an important insight that earthquakes occur only when the frictional strength of the fault (the sandpaper) weakens more rapidly than elastic energy is relaxed (the contracting spring).
Thin Viscous Sheet
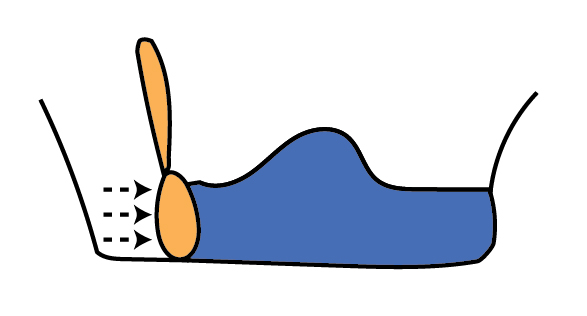Next time you make a very thick wintery soup, push it side to side with your spoon, making a mound, and notice how long it takes for the mound to spread out again. To make a large mound, you will need to make a very viscous soup and to move your spoon quickly. This is similar to the mathematical thin viscous sheet model, where the ‘thin’ label refers to the assumption that there are no shear stresses acting on the fluid, meaning it can only deform horizontally (as we push it) and up or down (due to mass conservation and gravity), and that the fluid’s properties do not vary vertically. Despite the simplicity of these assumptions, this model was developed to model mountain building during the India-Asia collision and reveals how to quantify the competition between the growth of mountains, due to far-field tectonic forces, and their tendency to spread apart under gravity.
Stress Around an Inclusion
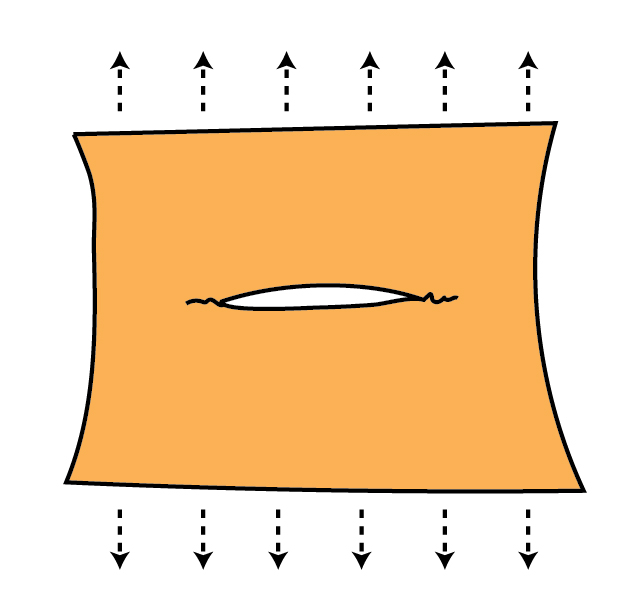If you make a tear in a piece of paper and then pull perpendicular to the cut, you’ll find that when a particular force is applied the tear will grow. The growth of the tear occurs because the force is focussed at the tip of the tear. Start with a larger tear and you will need to apply less force to make it grow, demonstrating that the focusing of force at the tear tip depends on the tear length. This can be mathematically modelled as an ellipsis shaped hole in an elastic material, where the stress around the hole can be calculated exactly (using Eschelby’s solution). These solutions can be used to understand how earthquake ruptures grow and how stresses change after an earthquake. Replace the hole instead with a relatively strong material and the same equations can be used to understand the deformation of rigid clasts in shear-zones or how much a magma can crystalise before it behaves like a solid.
Blocks in a Bath
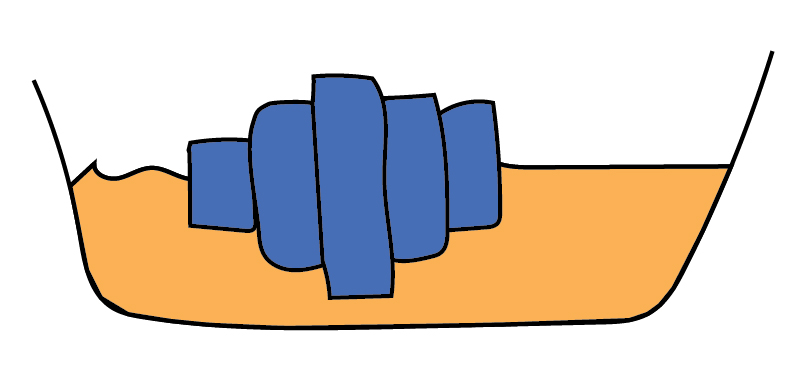Drop buoyant blocks of different thicknesses into a bath and they will float like icebergs, with different heights above the water. The Airy isostasy model makes the assumption that the lithosphere can move freely up or down in the mantle in the same way and involves a straight-forward calculation that links crustal thickness, density and topography. This model explains why thickening the crust leads to uplift and why old ocean basins are so deep underwater.
These are just a handful of well-known examples of simple toy models. They are surprisingly good at explaining how the Earth works, despite not looking very ‘realistic’, and provide hard numbers rather than just being visual aids. While high performance computing allows us to model very complex Earth processes, these toy models remain an important way to understand and apply the output from complex models, as well as to provide equations that provide reasonable approximations and can be easily applied by anyone without expensive computation. I hope readers may feel inspired to play around with these toy models and to maybe even reach for the pen and paper or the kitchen drawer next time you’re mulling over how the Earth works, rather than logging into a supercomputer (though they’re fun too!).
