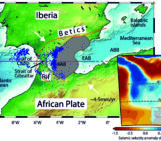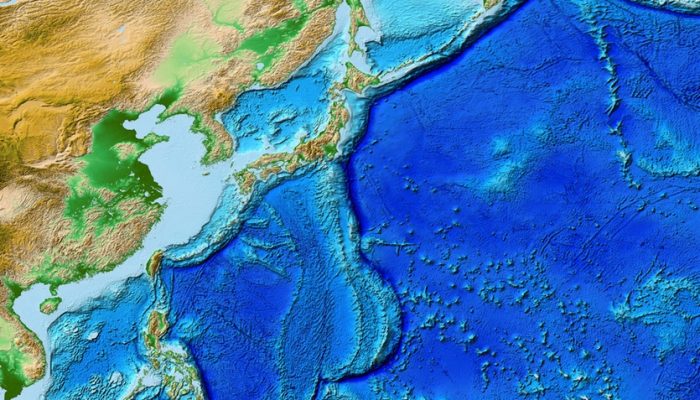
Subduction zones host one of the most complex and fascinating tectonic systems on the planet. Numerical models by Király and colleagues recently published in Earth and Planetary Science Letters reveal that the strength of the toroidal flow depends on the mantle viscosity and the magnitude of the slab pull force while the characteristic size of the toroidal cells mainly depends on the size of the convecting mantle.
The motion of Earth’s tectonic plates—the lithosphere—is driven by the subduction of relatively cold and dense oceanic plates into the mantle. Subduction zones are some of the most striking features on Earth. They represent one of the two types of convergent plate boundaries, in which one tectonic plate sinks underneath another one into the Earth’s mantle. The resulting forces induce mantle flow around the subducting plate, but the manner in which this happens is still a matter of debate.
Below the tectonic plates, the mantle moves in a slow and unseen manner—as cold slabs sink, hot upwellings rise, and convection slowly rids the Earth’s interior of its primordial heat. Much of our knowledge of mantle flow patterns is indirect, inferred from geodynamical models or seismic tomography images.
Seismological and geochemical investigations suggest 3D subduction-induced mantle flow around lateral slab edges from the sub-slab zone towards the mantle wedge[1]. Such flow has also been observed in laboratory experiments[2] and numerical models of subduction[3]. In particular, geodynamic numerical models of subduction demonstrate that back-arc extension at narrow subduction zones is driven by rollback-induced mantle flow[4].
Observations of seismic anisotropy—the directional dependence of seismic wave speed—provide us with tantalizingly direct information about mantle flow direction. For example, crystals of olivine, which is the most common upper-mantle mineral, tend to become aligned by the mantle flow, and seismic anisotropy is an indicator of this alignment.
To apply the laboratory-derived viscosity laws to nature, they must be extrapolated over 10 orders of magnitude, which introduces uncertainty. Moreover, it is unclear to what extent experiments on centimeter-scale samples are representative of the crust and lithosphere.
The viscosity distribution of the lithosphere and the surrounding mantle is therefore one of the least certain parameters in geodynamics. Alternative ways to determine viscosity on geological time scales are thus needed.
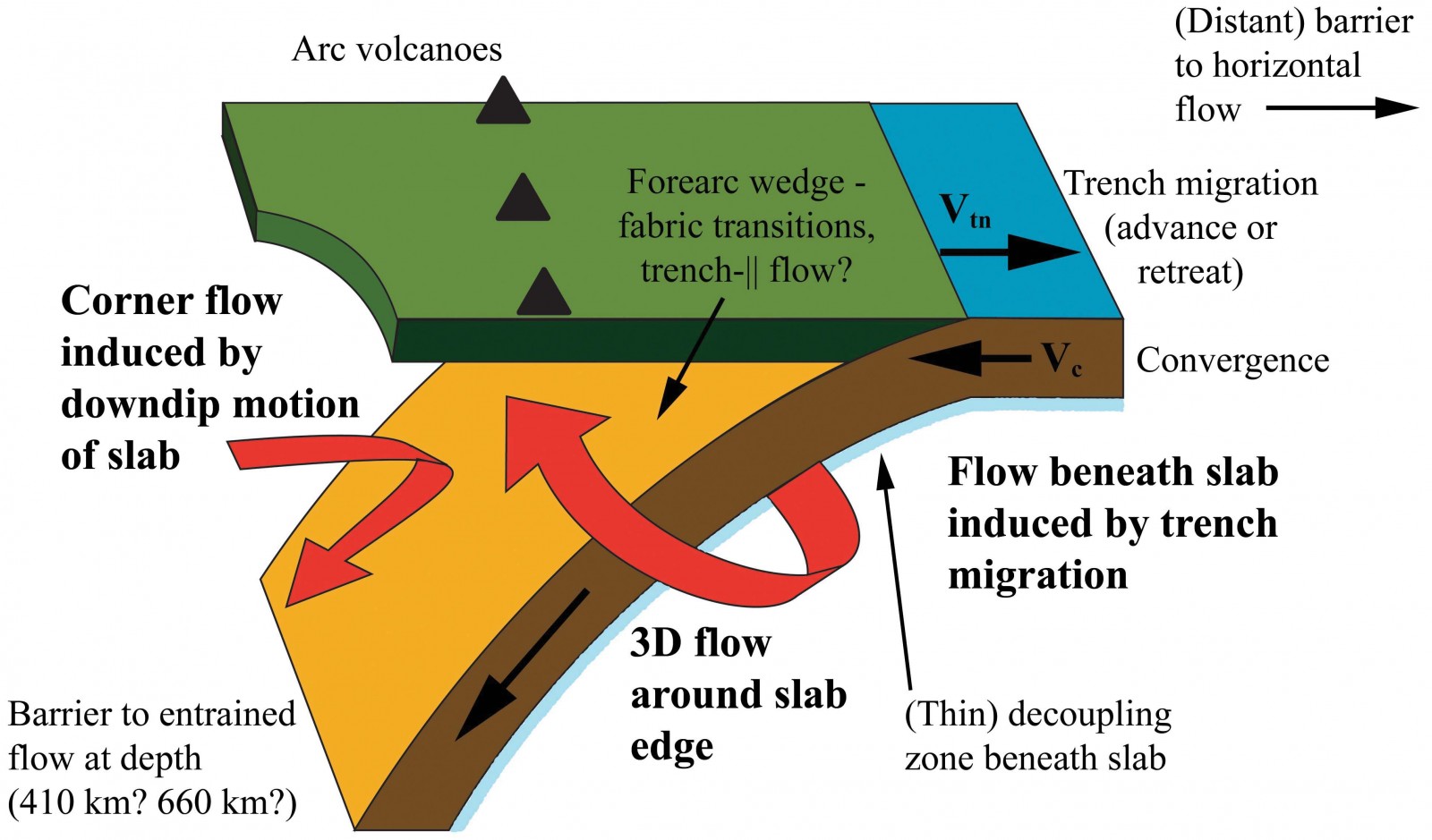
Schematic diagram of a subduction zone, showing the dominance of 3D flow beneath the slab and the competing influence of 2D and 3D flow fields in the mantle wedge. Credit: Long and Silver, 2008, Science.
Writing in Earth and Planetary Science Letters, Király and colleagues[5] present a cutting-edge numerical model that shows how the strength and length scale of the toroidal flow vary with the mantle viscosity and the magnitude of the slab pull force. Király and co-workers highlight some remarkable implications of these effects: around subducting plates, the characteristic length, axis, and shape of the toroidal cell are almost independent of the slab’s properties and mainly depend on the thickness of the convecting mantle. The independence of the shape of the toroidal cell on the slab width can appear controversial with respect to previous studies[6–7] that showed that the overall mantle flow is dependent on the slab width. However, as Király et al. point out, these differences can be explained with the model setup adopted and the range of slab widths investigated.
In order to characterize the flow—in terms of its geometry and strength—Király and co-workers analysed the vertical component of the mantle vorticity as well as the ratio between the vertical and the trench parallel component of the vorticity vector. With a series of numerical experiments, they find that subduction-induced mantle flow is highly three-dimensional, and that the toroidal component is sub-horizontal with some vertical flow components. According to the authors, this vertical flow around the slab edges has significant implications, as it can be responsible for the presence of the off-arc volcanism around several laterally confined subduction zones.
The numerical experiments by Király et al. represent another step forward in our understanding of how mantle circulation plays a relevant role in the shaping of tectonic features around subduction zones, and they provide evidence that the slab properties only impact the vigour of the flow around subducting slabs. The extension of these numerical experiments to a range of different parameters will allow for a fuller characterization of the olivine fabric, which in turn will allow seismologists to relate their measurements of seismic anisotropy to flow directions and, ultimately, to mantle processes.
References: 1. Long, M. D., and P. G. Silver (2008), The subduction zone flow field from seismic anisotropy: A global view, Science, 319, 315-318. 2. Funiciello, F., C. Faccenna, and D. Giardini (2004), Role of lateral mantle flow in the evolution of subduction systems: insights from laboratory experiments, Geophy. J. Int., 157, 1393-1406. 3. Jadamec, M. A., and M. I. Billen (2010), Reconciling surface plate motions with rapid three-dimensional mantle flow around a slab edge, Nature, 465, 338-342. 4. Sternai, P., L. Jolivet, A. Menant, and T. Gerya (2014), Driving the upper plate surface deformation by slab rollback and mantle flow, Earth Planet. Sci. Lett., 405, 110-118. 5. Király, A. Capitanio, F.A., Funiciello, F., Faccenna, C. (2017). Subduction induced mantle flow: Length-scales and orientation of the toroidal cell. Earth Planet. Sci. Lett., 479, 284–297. 6. Funiciello, F., Moroni, M., Piromallo, C., Faccenna, C., Cenedese, A., Bui, H.A., 2006. Mapping mantle flow during retreating subduction: laboratory models analyzed by feature tracking. J. Geophys. Res., Solid Earth 111, 1–16. 7. Stegman, D.R., Freeman, J., Schellart, W.P., Moresi, L., May, D., 2006. Influence of trench width on subduction hinge retreat rates in 3-D models of slab rollback. Geochem. Geophys. Geosyst. 7.