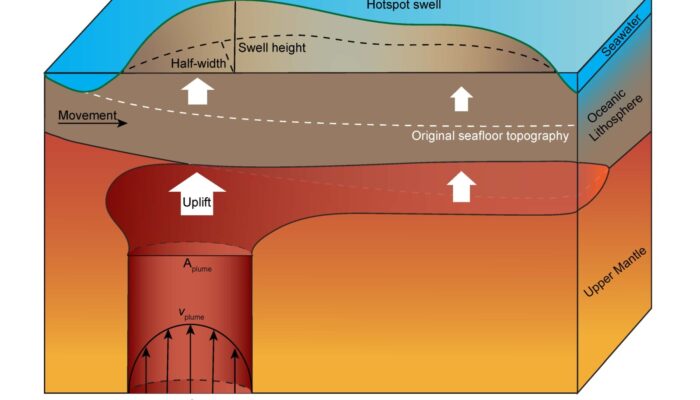
Figure 1. Illustration of the hotspot swell and plume buoyancy flux. White dashed line shows the original seafloor topography due to half-space cooling. Dark green line represents the surface dynamic topography caused by the dynamic uplift of the plume.
One of the main surface expressions of dynamic topography are hotpot swells formed by mantle plumes. In this week’s post, Ziqi Ma, PhD candidate at University College London (UK), discusses how to use geodynamic numerical models to understand the links between plume buoyancy flux and dynamic topography.
Mantle convection and plate motion control Earth’s dynamic evolution (Cande & Stegman, 2011; Stern & Gerya, 2018). Mantle plumes—hot upwellings that transport heat from Earth’s core to the base of the lithosphere—serve as crucial agents in this process, while also sampling the chemical structure of the lowermost mantle. A key metric, plume buoyancy flux, measures the mass and heat that mantle plumes transfer to the surface (Figure 1).
However, global estimates of plume buoyancy fluxes still remain a topic of debate (Hoggard et al., 2020; King & Adam, 2014; Ribe & Christensen, 1999). Previous studies have calculated the plume buoyancy flux from the geometry of the hotspot swell—topographically high regions that are diagnostic surface expressions of mantle plumes, characterized by elevations of up to 2-3 km and widths of ~1500 km. These calculations typically assume that the asthenosphere moves at the same velocity as the overriding plate (Sleep, 1990). However, at least some plumes (e.g., Iceland) can move faster than the corresponding plate motion (Poore et al., 2011). With increasingly available observational constraints for dynamic seafloor topography (Hoggard et al., 2021; 2020), it is time to refine global estimates of plume buoyancy fluxes and update the scaling law between surface dynamic topography and plume buoyancy flux.
Here, we conduct thermomechanical models to study plume-lithosphere interaction and hotspot swell support. We use the finite-element code ASPECT in a high-resolution, regional, 3D Cartesian framework (Heister et al., 2017; Rose et al., 2017). We adopt a composite diffusion-dislocation creep rheology and a free-surface boundary at the top.
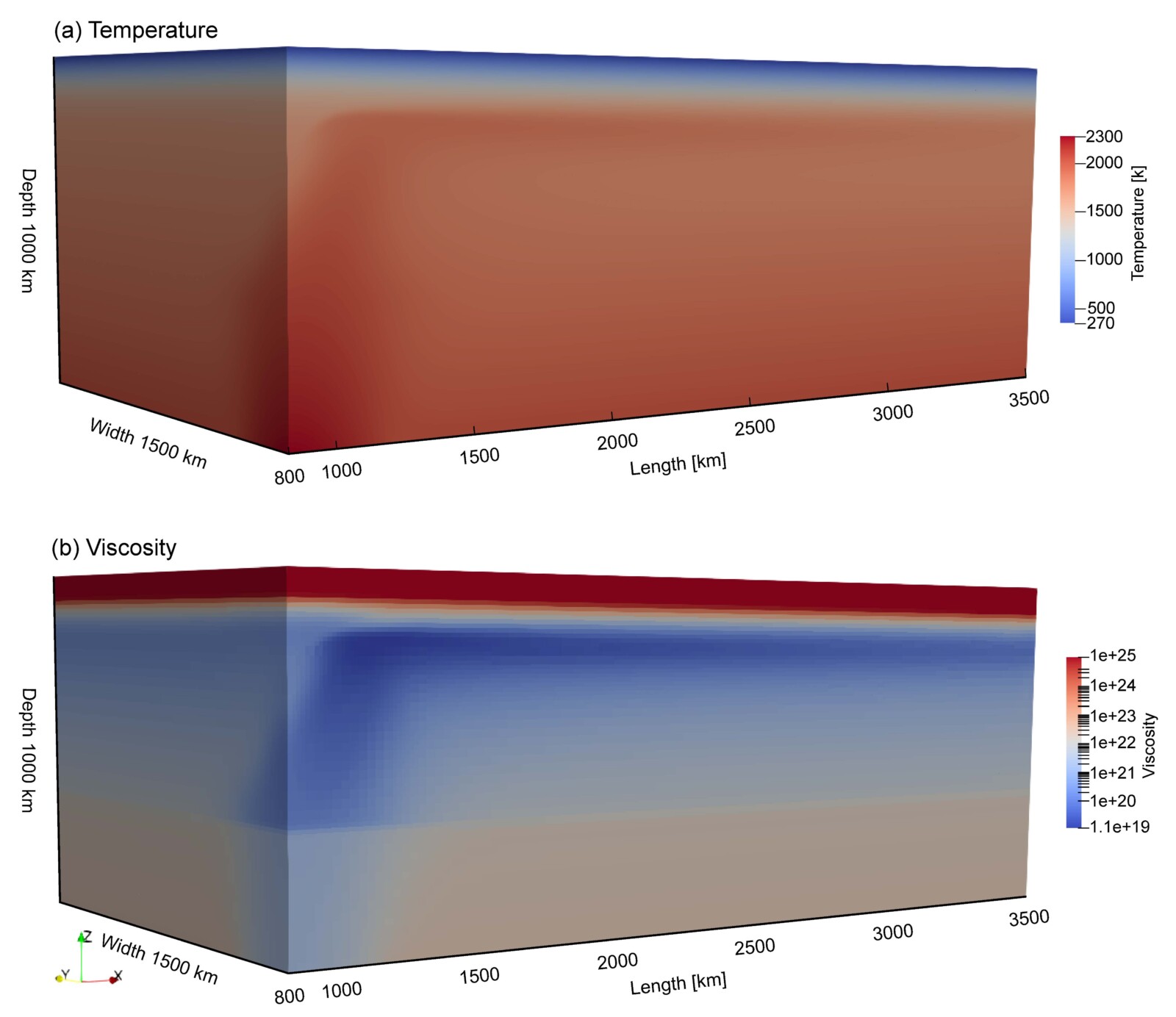
Figure 2. Model results at 200 Myr. (a) The temperature profile; (b) The viscosity profile.
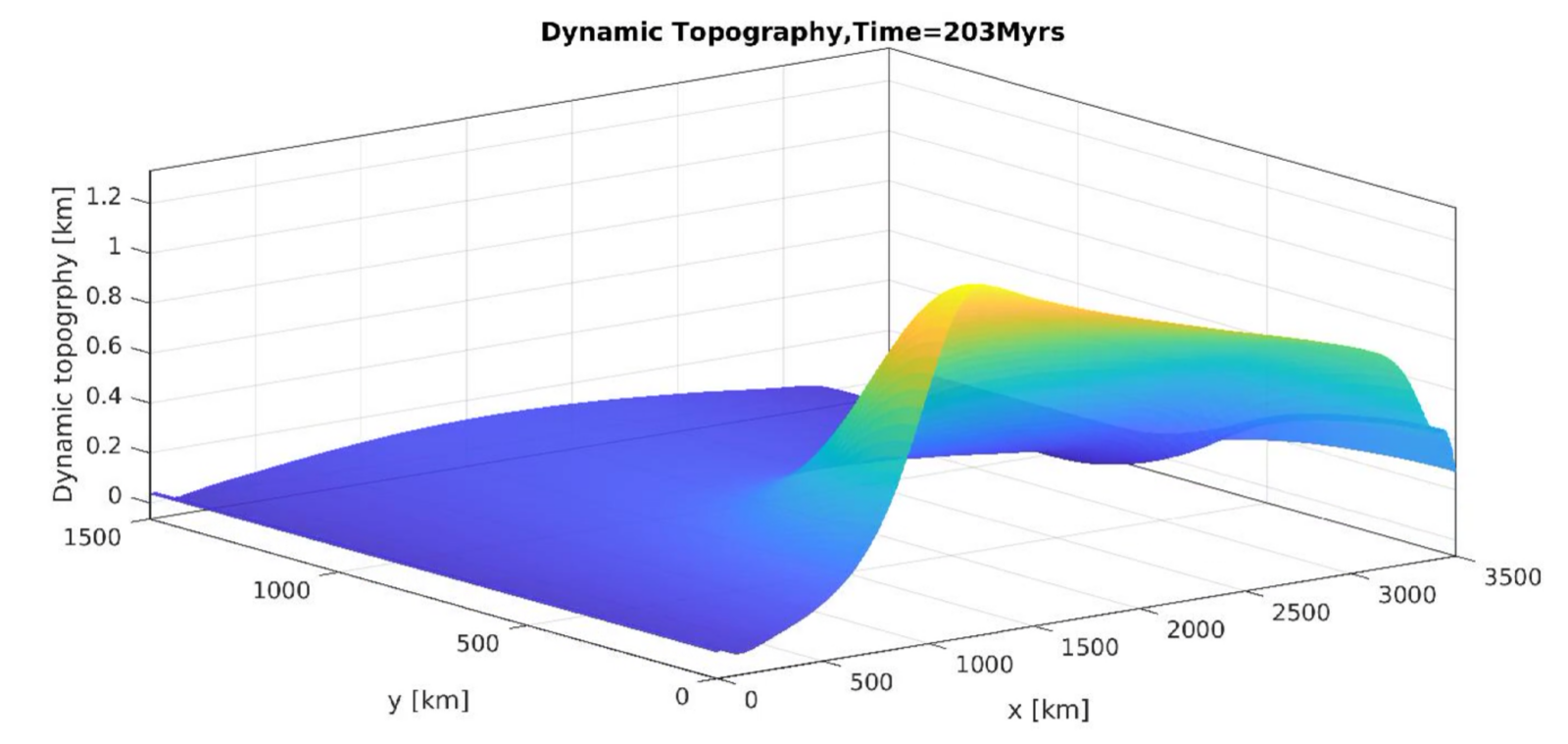
Figure 2 shows the temperature and viscosity profiles of our reference case at 200 Myr, where the plume penetrates the Mantle Transition Zone at 660-km depth and rises through the upper mantle, reaches the base of the lithosphere, spreads out laterally like a pancake, and exits the right boundary of the model. Figure 3 is a snapshot of our reference case, demonstrating the surface dynamic topography primarily due to plume-induced dynamic uplift, because we removed the descent caused by half-space cooling and accounted for the seawater density in the calculations.
Figure 3. Snapshot of the surface dynamic topography considering the seawater density at 203 Myrs.
We investigated the effects of plume excess temperature and plume radius on swell topography. From these results for plume spreading beneath moving plates, the buoyancy fluxes of individual plumes (like Hawaii), as well as the relevant plume temperatures and radii, are quantitatively constrained. Our preliminary models reveal that:
-
For a fixed plume radius, higher plume excess temperature results in higher swell;
-
Higher plume excess temperature lead to decreasing swell half-width at low plume radii, making the swell more pointy than flat.
-
Plume buoyancy flux is linearly proportional to swell , as shown in Figure 4:
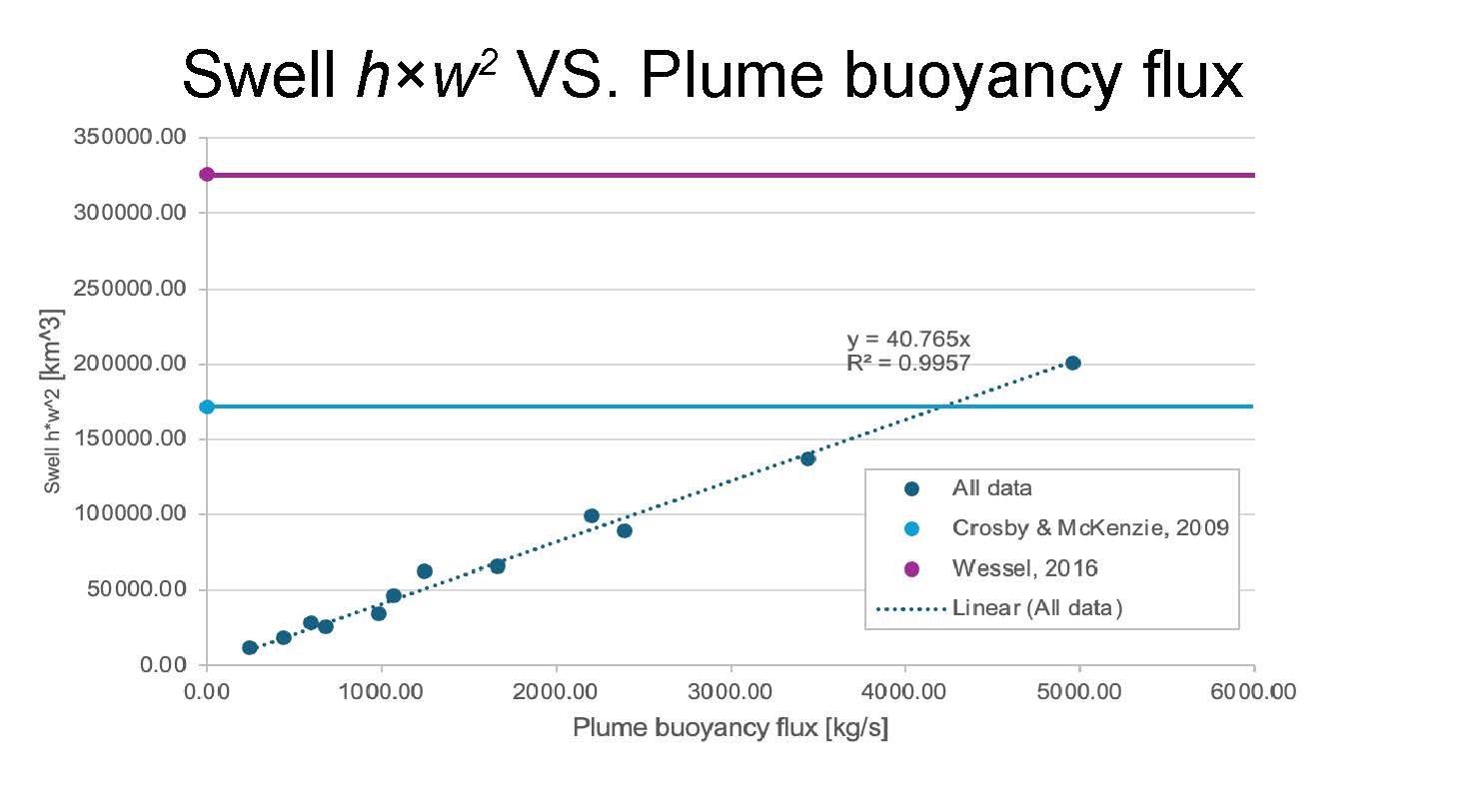 Figure 4. Scaling between the swell topography and plume buoyancy flux. Purple line denotes the observed swell shape from Wessel, 2016. Blue line represents the observed swell shape from Crosby & McKenzie, 2009.
Figure 4. Scaling between the swell topography and plume buoyancy flux. Purple line denotes the observed swell shape from Wessel, 2016. Blue line represents the observed swell shape from Crosby & McKenzie, 2009.
Our findings suggest that previous swell-based estimates might underscore the true buoyancy fluxes of the underlying plume upwelling (Figure 4). However, melt can significantly impact the swell topography (Ribe & Christensen, 1999) and must be considered in our future model to refine these estimates further.
Ziqi Ma, PhD student from department of Earth Sciences, University College London.
“After I earned my Master’s degree in Geodynamic Numerical Modeling from the Institute of Geology and Geophysics, Chinese Academy of Sciences, I chose to pursue a PhD in the same field driven by a deep passion for Earth sciences and a relentless curiosity. Moving to London was not only a childhood dream come true for a Harry Potter fan like me but also a significant challenge. I must admit, it took some time to adapt to the new culture. Fortunately, during my studies at UCL, my supervisor, Dr. Maxim Ballmer, and collaborator, Dr. Antonio Manjón-Cabeza Córdoba, have been incredibly supportive, offering invaluable guidance in both my research and life. Over the past two years, I have been fortunate to travel to several beautiful locations, including Vienna in Austria, Haltern am See in Germany, and Sète in France, to present my work and more importantly, make lots of friends. These experiences have deepened my appreciation for the importance of collaborative research and the rich cultural exchange that comes with it.”
References Cande, S. C., & Stegman, D. R. (2011). Indian and African plate motions driven by the push force of the Réunion plume head. Nature, 475(7354), 47–52. https://doi.org/10.1038/nature10174 Crosby, A. G., & McKenzie, D. (2009). An analysis of young ocean depth, gravity and global residual topography. Geophysical Journal International, 178(3), 1198–1219. https://doi.org/10.1111/j.1365-246X.2009.04224.x Heister, T., Dannberg, J., Gassmöller, R., & Bangerth, W. (2017). High accuracy mantle convection simulation through modern numerical methods-II: realistic models and problems. Geophysical Journal International Geophys. J. Int, 210, 833–851. https://doi.org/10.1093/gji/ggx195 Hoggard, M., Austermann, J., Randel, C., & Stephenson, S. (2021). Observational Estimates of Dynamic Topography Through Space and Time. Mantle Convection and Surface Expressions, May 2020, 373–411. https://doi.org/10.1002/9781119528609.ch15 Hoggard, M. J., Parnell-Turner, R., & White, N. (2020). Hotspots and mantle plumes revisited: Towards reconciling the mantle heat transfer discrepancy. Earth and Planetary Science Letters, 542, 116317. https://doi.org/10.1016/j.epsl.2020.116317 King, S. D., & Adam, C. (2014). Hotspot swells revisited. Physics of the Earth and Planetary Interiors, 235, 66–83. https://doi.org/10.1016/j.pepi.2014.07.006 Poore, H. R., White, N., & MacLennan, J. (2011). Ocean circulation and mantle melting controlled by radial flow of hot pulses in the Iceland plume. Nature Geoscience, 4(8), 558–561. https://doi.org/10.1038/ngeo1161 Ribe, N. M., & Christensen, U. R. (1999). The dynamical origin of Hawaiian volcanism. Earth and Planetary Science Letters, 171(4), 517–531. https://doi.org/10.1016/S0012-821X(99)00179-X Rose, I., Buffett, B., & Heister, T. (2017). Stability and accuracy of free surface time integration in viscous flows. Physics of the Earth and Planetary Interiors, 262, 90–100. https://doi.org/10.1016/j.pepi.2016.11.007 Sleep, N. H. (1990). Hotspots and Mantle Plumes: Some Phenomenology. Geology, 95, 6715–6736. Stern, R. J., & Gerya, T. (2018). Subduction initiation in nature and models: A review. Tectonophysics, 746(February 2017), 173–198. https://doi.org/10.1016/j.tecto.2017.10.014 Wessel, P. (2016). Regional-residual separation of bathymetry and revised estimates of Hawaii plume flux. Geophysical Journal International, 204(2), 932–947. https://doi.org/10.1093/gji/ggv472