The uncertain tomographic lenses

The SOLASW3D model (credit: author)

Geodynamicists often try to answer scientific questions related to the Earth interior, but direct observations of such depths are rather limited–unless you are character in a Jules Verne’s novel or a prominent scientist in the movie The Core–. A way to deal with this issue is to rely on indirect methods, with seismic tomography being one of the most widely used by geoscientists. However, as any observational method, seismic tomography comes with their limitations and uncertainties, which are often overlooked or not easily understandable by non-tomographers. In this week’s post, Franck Latallerie, a postdoc at University of Oxford (UK), shares his thoughts on how we can better use seismic tomography to validate geodynamic interpretations.   

Franck Latallerie is postdoctoral researcher in seismology at University of Oxford (UK). He is currently working with the MC2 group (Mantle Circulation Constrained, Large NERC grant). His research focuses on the structure and dynamics of the Earth’s interior. In particular, Franck investigates novel methods to constrain the limitations of tomography models. You can contact him via email

What is the value of a geodynamic simulation if it doesn’t match certain sets of observations? On the other hand, what is the value of some observations if we cannot fit a physical model on it? When it comes to mantle convection in the Deep Earth, seismic tomography proves to be a powerful tool to constrain geodynamic simulations as it broadly maps 3D structures. However, the plot is not that simple: Tomographic images are not simple pictures of the Earth’s interior. When I started working on seismic tomography, I was told by a wise tomographer (she might recognise herself): “The one who believes the least in a tomographic model is the one who made it.” It is not because tomographers don’t do a good job; it is because we know what are the inherent limitations from the data. This is fine, as long as these limitations are accounted for in subsequent studies using tomographic models. However, it seems not to be always the case. But the seismological community seems to be working towards a better assessment of tomographic limitations. I believe this is an important point, even if some might find it bothering. I like this quotation from Scales and Snieder in ‘To Bayes or not to Bayes’, 1997: “A common complaint we hear is that people do not want to hear about ranges of models, error bars, or all this messy statistics.” Well.. this blog post is about them. 

“The one who believes the least in a tomographic model is the one who made it.”

Do we need lenses?

As seismic waves generated by earthquakes travel through the Earth’s interior they sample its physical properties. These properties can be inferred back by looking at seismograms recorded at the surface. However seismic stations are poorly distributed (Figure 1). They are installed mostly on continents, and in the northern hemisphere. The southern hemisphere, oceans, and remote regions such as the poles remain poorly instrumented. Seismic sources also are poorly distributed. They occur mostly in geologically active regions at plate boundaries, particularly in subduction zones. With this in mind, we can ask ourselves: what’s the value of a tomographic estimate (for example S-wave velocity) in a region that has not been traversed by seismic waves? The fact that tomographic models are presented as continuous maps is misleading, and we easily forget that some regions are less well constrained than others, eventually hampered by strong artefacts. This leads us to the concept of resolution (Figure 2).   

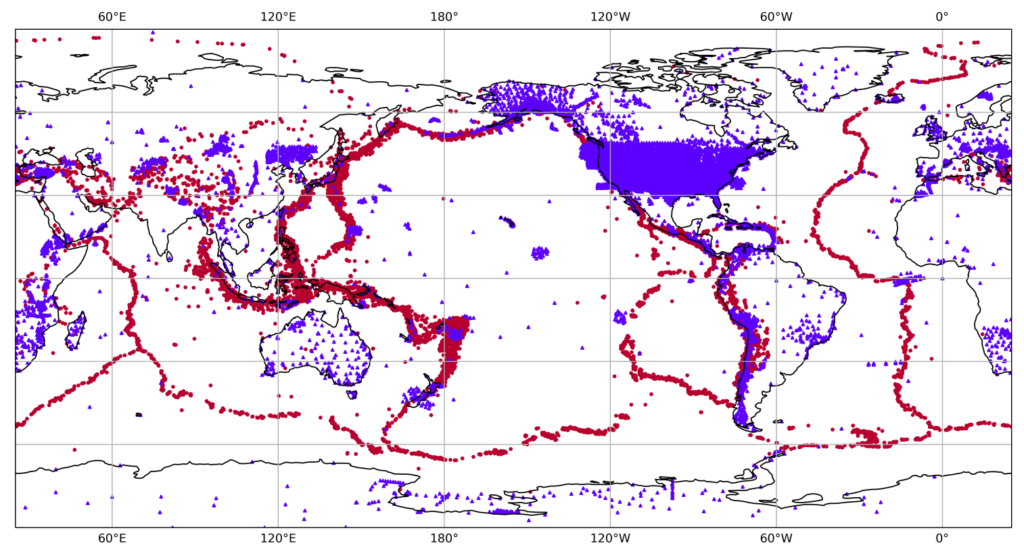
Figure 1: A representative distribution of earthquakes (red circles, from the GCMT catalog), and seismological stations (blue triangles, from the Earthscope consortium).

The resolution of a tomography model can be seen (at least in a linear case) as a set of local averages. Each estimated value in a tomographic model (S-wave velocity in a cell for example) is in fact a spatial average over all the values of the whole ‘true’ model. In general, we want the spatial average to be as local as possible around the point of interest; but our ability to do so will be dictated by the data. For example, a location that has not been covered by any ray will have a huge averaging region! Moreover, the resolution not only changes in size, but also in shape. What would be the effect of a smeared local average? What if the average is completely shifted, actually averaging a region far away from the point of interest? 

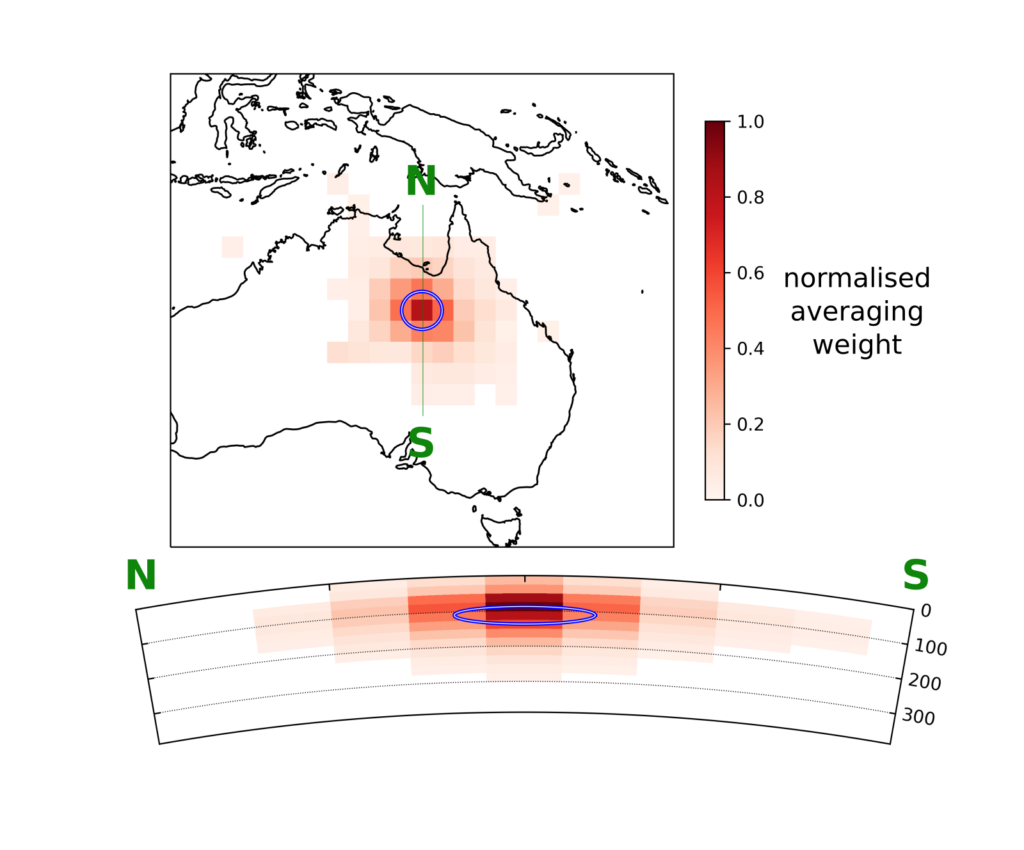
Figure 2: Resolution for a point in the SOLASW3D tomography model. The colorscale indicates the averaging weight (normalized by the maximum), and the blue circles indicate the extent of the target resolution (Latallerie et al., in prep).

As beautifully termed by Zaroli (2016), resolution acts as ‘lenses’ that we would use to look through the interior of the Earth; but these lenses are poorly designed, and they can be highly misleading. Accounting for resolution for interpreting tomographic models is crucial. Coming back to geodynamics, if we want to compare a geodynamic prediction with tomographic observations, then it becomes clear that we need to account for resolution effects. If the resolution is known, then it can be applied to the geodynamic prediction (which means applying the local averaging for each location in the prediction), a technique called ‘tomographic filtering’ (Ritsema et al., 2007). This way we are looking at the ‘true’ Earth and at the geodynamic prediction with the same lenses: so yes, we need lenses. 

“resolution acts as ‘lenses’ that we would use to look through the interior of the Earth; but these lenses are poorly designed, and they can be highly misleading”

Do we need certainty? 

Even if we say we build tomographic ‘models’, seismic tomography is an observational discipline. This is important as it reminds us that, as in any observational field, our observations are affected by errors. Sources of error are all processes affecting the data that we do not account for when interpreting them. They are infinitely many; some are negligible, but some are not. How did we design the time window or the filtering processes? What about off-ray sensitivity in ray-theory, or non-linear effects in a linear framework? What if someone stepped next to a seismometer as seismic waves were arriving? Usually we don’t know what is the exact value of an error, but we may be able to describe it with probabilities: for instance instead of stating that the velocity at some location is 5km/s, we may prefer stating that there are 95% chances that the velocity is within 5 +/- 0.1 km/s. How robust is a feature in a tomography model, say a blob 1% faster than average, if the uncertainty on it is 2%? Without robust uncertainty estimates, we could be tempted to interpret every such little blobs which may not be robust. Coming back to geodynamics, we may want to compare a geodynamic prediction (after applying the tomographic filter ‘lens’ to it..) to a tomographic model. In a similar way, what’s the value of a prediction that fails to reproduce an observed feature that is highly uncertain? It would be unfair to penalize a prediction failing to reproduce an uncertain feature: thus, we need uncertainty. 

Going to a better optician: how can we get lenses and uncertainty?

The tomography community is working towards better account for tomographic resolution and uncertainty. This has been a main focus of my research and the work of close colleagues in Oxford (e.g. Sam Scivier using gaussian processes methods for merging models, Adrian Mag using SOLA for the core-mantle boundary (CMB) topography, Justin Leung making geodynamic assessment with resolution-uncertainty, etc.). As a ‘surface-wave’ seismologist, I build tomography models of the upper-mantle. My goal over the last few years has been to apply an approach to surface-wave tomography called the ‘Subtractive Optimally Localised Averages’ (SOLA) method. Its power is to provide some control over the resolution and uncertainty and to produce all this information easily. The origin of this approach is the theory formulated by the geophysicists Backus and Gilbert who recognized in the 60’s that the concepts of resolution and uncertainty are important for deep Earth studies (Backus and Gilbert 1967, 1968, 1970). SOLA was formulated later by the seismologists Pijpers and Thompson for helioseismology (i.e., study of the interior of the Sun from observations of its oscillations; Pijpers and Thompson 1992, 1993), and it was recently introduced in seismology by Christophe Zaroli (Zaroli 2016), who has introduced me to this method during my PhD in Strasbourg. 

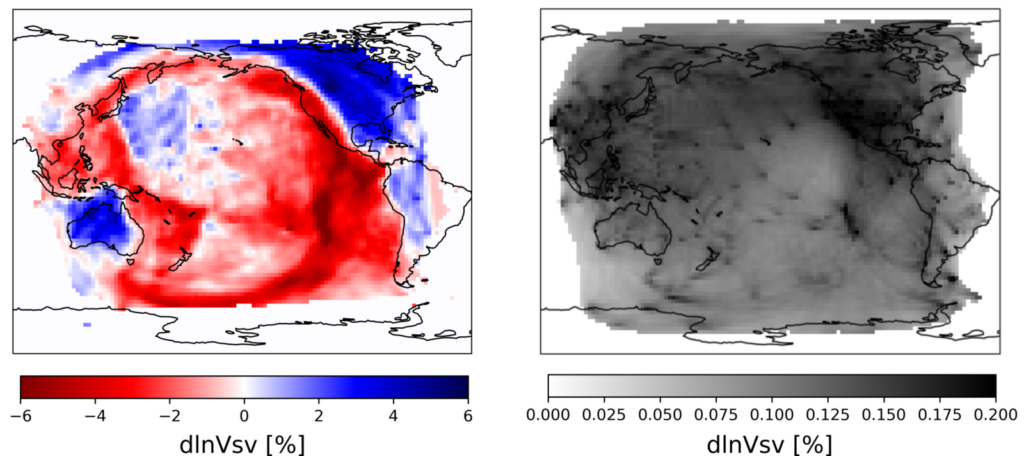
Figure 3: The SOLASW3D model: (left) model solution, (right) model uncertainty. Unit is perturbations of SV-wave velocity with respect to a 1D radial reference model. (Latallerie et al., in prep).

Beyond interpreting the tomography models themselves (within their limitations), we can use them to discuss geodynamical predictions. Currently, I am collaborating on these topics with geodynamicists in Cardiff. My work consists in filtering their predictions and comparing them to the tomography models accounting for the tomographic uncertainty. This helps us to learn about what input parameters in their simulations best match tomographic observations and refine our estimates for some physical parameters in the Earth.  

 In summary, seismic tomography is a powerful tool to map the interior of the Earth, but tomography models have their limits. Equipped with the tomographic lenses and uncertainties will help to draw robust inferences about processes occurring in the Earth interior. 

If you do have some geodynamic prediction that you would like to compare with tomography, I provide tomography models with their resolution and uncertainty (Figure 3) in my website here. There are explanations and code snippets, for example to apply the tomographic filter to your predictions yourself. 

References

Backus, G. & Gilbert, F. (1968). The resolving power of gross Earth data, Geophys. J. Int., 16(2), 169–205.

Backus, G. & Gilbert, F. (1970). Uniqueness in the inversion of inaccurate gross Earth data, Phil. Trans. R. Soc. A, 266(1173), 123–192. 

Backus, G.E. & Gilbert, J.F. (1967). Numerical applications of a formalism for geophysical inverse problems, Geophys. J. Int., 13(1–3), 247–276. 

Pijpers, F. P., & Thompson, M. J. (1992). Faster formulations of the optimally localized averages method for helioseismic inversions. Astronomy and Astrophysics, 262:33–36. 

Pijpers, F. P., & Thompson M. J. (1993). The SOLA method for helioseismic inversion. Astronomy and Astrophysics, 281:231–240. 

Scales, J.A. & Snieder, R., (1997). To Bayes or not to Bayes?, Geophysics, 62(4), 1045–1046. 

Ritsema, J., McNamara, A. K., & Bull, A. L. (2007). Tomographic filtering of geodynamic models: Implications for model interpretation and large-scale mantle structure. Journal of geophysical research, 112(B01303), 8. 

Zaroli, C. (2016). Global seismic tomography using Backus-Gilbert inversion. Geophysical Journal International, 207(2), 876–888. 

Zaroli, C., Koelemeijer, P., & Lambotte, S. (2017). Toward seeing the Earth’s interior through unbiased tomographic lenses, Geophys. Res. Lett., 44(22), 399–11 

Latallerie, F., Zaroli, C., Lambotte, S., & Maggi, A. (2022). Analysis of tomographic models using resolution and uncertainties: a surface wave example from the Pacific. Geophysical journal international, 230(2), 893–907. 

G. Ekström, M. Nettles, and A.M. Dziewoński. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Physics of the Earth and Planetary Interiors, 200-201:1–9, June 2012. ISSN 00319201. doi: 10.1016/j.pepi.2012.04.002. URL https://linkinghub.elsevier.com/retrieve/pii/S0031920112000696. 

Seismic source solutions were downloaded from the Global Centroid Moment Tensor Catalog GCMT www.globalcmt.org (Ekstrom et al., 2012). The facilities of EarthScope Consortium were used for access to waveforms and related metadata and derived data products. These services are funded through the National Science Foundation’s Seismological Facility for the Advancement of Geoscience (SAGE) Award under Cooperative Agreement EAR-1724509.