The field of rock rheology may seem a bit ‘odd’ at first glance to those geoscientists who are vaguely familiarized with the topic of geodynamics. Often, rocks are considered massive and competent geomaterials that display a sudden (and sometimes violent) brittle failure (earthquake alert!). However, when considering the high temperatures and large timescale characteristics of most geodynamic processes, it can be safely assumed that rocks flow in a ductile manner. Hence, it is very important for geoscientists to have a grasp on the basic rheological relations/models that can be subsequently applied to rocks, in order to best capture their ductile viscous behavior. In this Geodynamics 101 blog post, we are going to walk through some of the basic concepts of rock rheology!
How is rheology defined?
First and foremost, the field of rheology is essentially the study of time-dependent stress-strain behavior of a material (Jaeger et al. 2007), in our case the focus are rocks. A bit of word etymology: the word rheology originates from the Greek words rhei (ρέει or ρέω), meaning flow, and logos (λόγος), meaning study (Jaeger et al. 2007). Since we are interested in million-year geodynamic processes, it is essential to discuss a very important plastic time-dependent deformation mode, which is none other than creep. The general definition of the latter is best given by Gerya (2010) in his go-to book for any geodynamics fellow, where he explicitly states that: ”… Solid-state creep is the ability of crystalline substances to deform irreversibly under applied stresses. …”.
The creep behavior of a material can be divided into three distinct stages: primary, secondary, and tertiary creep (Fig. 1). During the primary or transient creep stage the strain increases with a decreasing rate. When the strain rate becomes constant the transition to the secondary or steady-state creep stage occurs. Finally, the tertiary creep stage starts when the strain rate increases in an exponential manner, ultimately leading to the failure of the material.
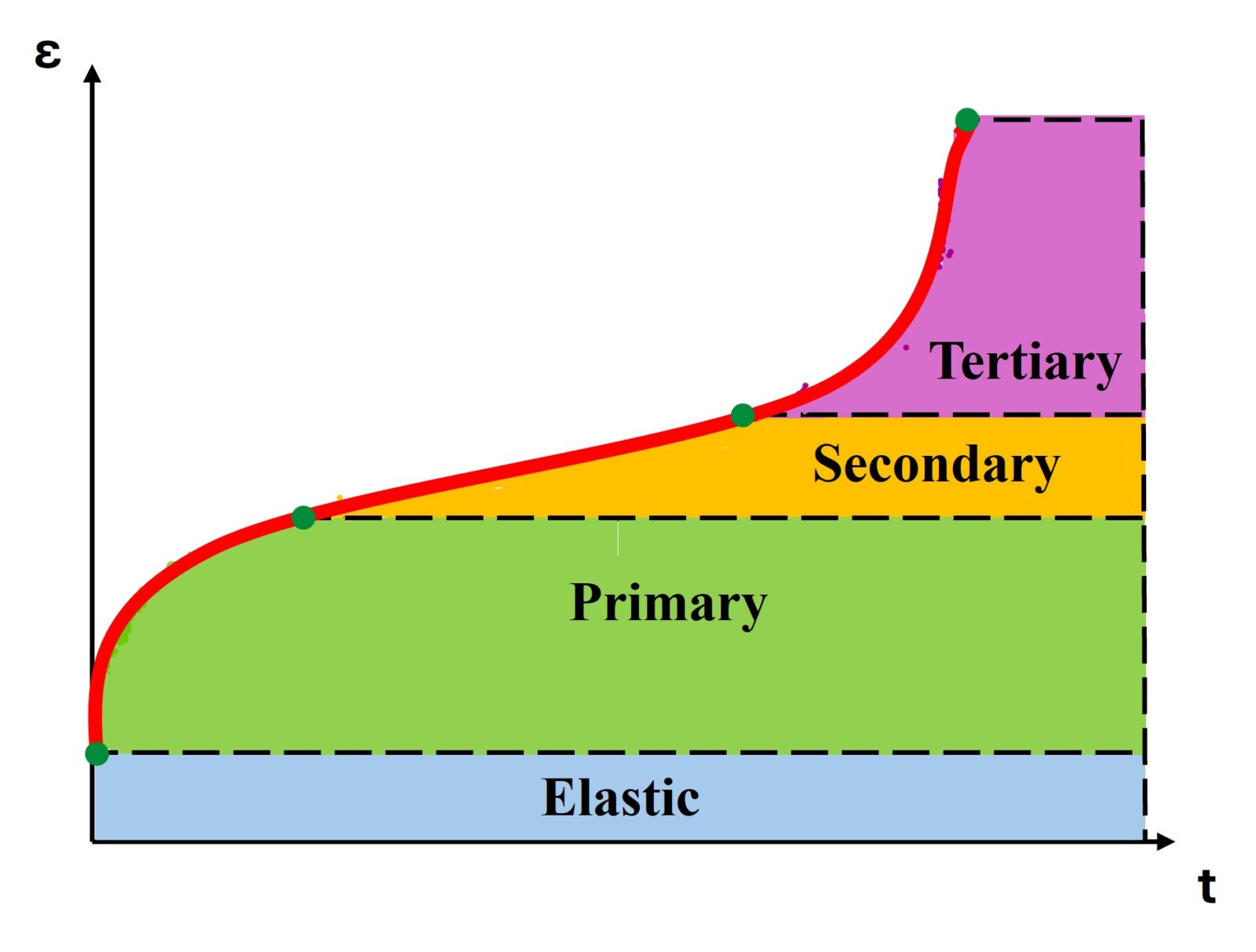
Fig. 1. The characteristic creep curve of a material, where the strain (ε) is plotted as the function of the time (t) (credit: Author).
Mechanical analogues of viscoelastic relations
For the sake of simplicity, the different rheological behaviors can be represented using springs, dashpots, and sliders, where each of these accounts for a different deformation response of the rock. Hookean springs represent the elastic deformation; dashpots, the Newtonian viscous deformation (note: a fluid is characterized as Newtonian when the shear stress is linearly proportional to the strain rate), and finally sliders account for the inelastic/plastic response of the rock.
A step up in complexity involves combining the previously-mentioned mechanical analogues, which gives rise to various basic linear viscoelastic, viscoelastic-perfectly plastic, and viscoelastic-brittle plastic models. The two most simple linear viscoelastic rheological models are the Maxwell and Kelvin models. The former is composed of a spring and a dashpot in series, while the last connects a spring and a dashpot parallel (Fig. 2a-b). At this point one may wonder the following: is there really a big difference between the two aforesaid models? Since at the end of the day both are comprised of a spring and a dashpot, the only thing that differentiates them is the way the two mechanical analogues are connected (i.e., in series or in parallel). Well, this seemingly ‘simple’ connection difference ultimately accounts for drastic deviations in both the mathematical relations, as well as the creep behavior of the two models.
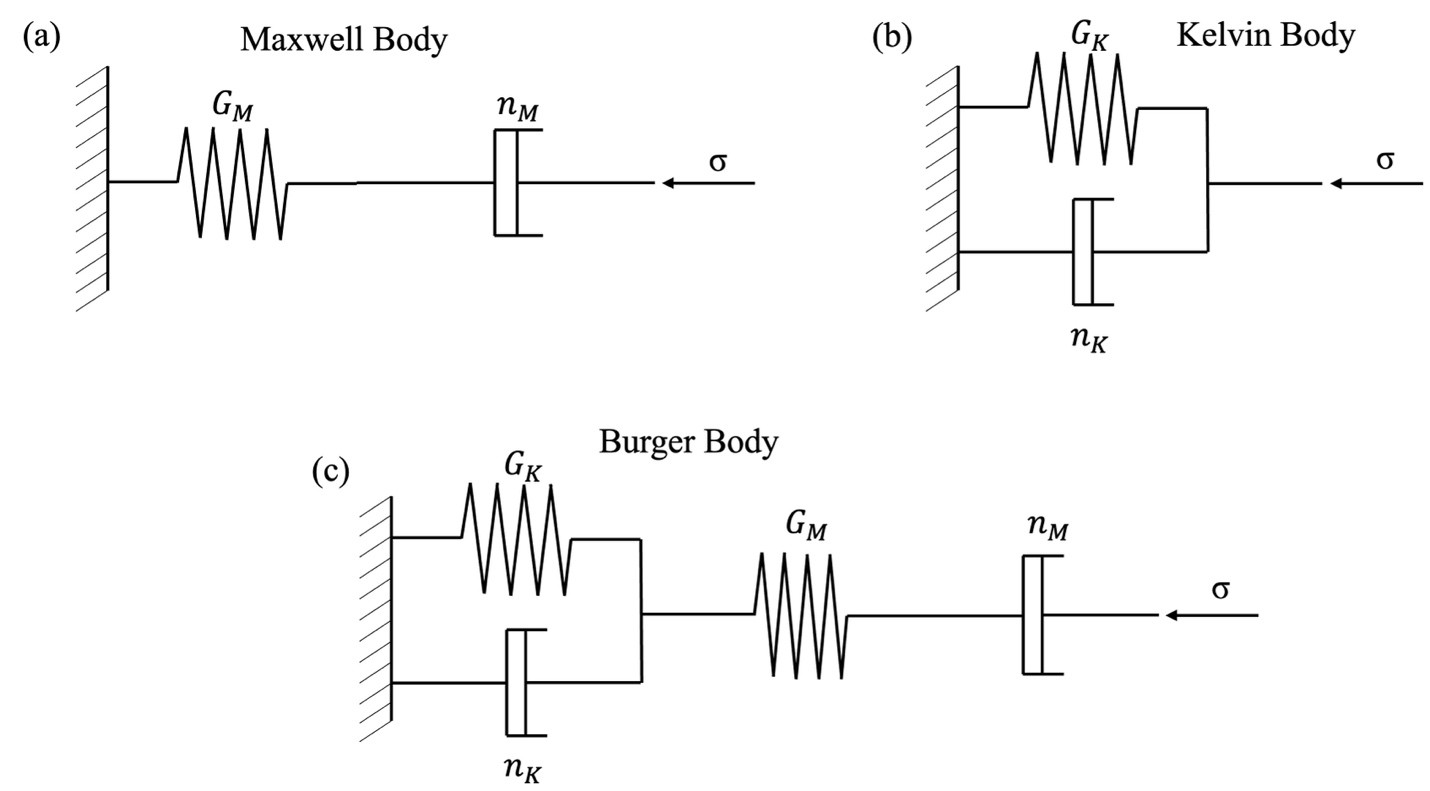
Fig. 2. Linear viscoelastic materials (a) the Maxwell body; (b) the Kelvin body; (c) the Burger body (credit: Author).
Under a constant exerted load, Maxwell’s model displays an immediate elastic response followed by an increasing secondary creep. In this body, the total strain rate is the sum of the strain rate caused by the elastic and the viscous deformation. On the other hand, Kelvin’s model under a constant applied load will have an asymptotically increasing strain that best captures the primary creep stage. The total stress of a Kelvin body can be obtained by summation of the stresses exerted on the spring and the dashpot, respectively. Don’t worry, I won’t drown you with the constitutive equations, but these can be found in the classical books of Ranalli (1995), Jaeger et al. (2007), and Gerya (2010), amongst many others.
Despite the simplicity of the previous two linear viscoelastic models, they have been adopted in the past by researchers to model geodynamic processes (e.g., Poliakov et al. 1993; Kaus and Becker 2007; Burov and Molnar 2008). More complicated linear viscoelastic models can be created by connecting in series a Maxwell and a Kelvin body (Fig. 2c), giving rise to the Burger body which can exhibit both primary and secondary creep.
Plastic deformation
So far, I haven’t included plasticity in our discussion; to do so a failure criterion must be incorporated in the rheological relations. The most commonly used, due to its simple linear relation, is the Mohr-Coulomb failure criterion. Other frequently used criteria, are the von Mises, Tresca, Griffith, and the Hoek-Brown failure criteria (see the books of Brady and Brown 2006; Jaeger et al. 2007). So, what happens when the material reaches its peak strength? It yields and enters its post-peak behavior region. The two often used relations to describe the material’s response in its residual strength region are the perfect plastic and the brittle plastic approximations (Fig. 3). The former considers that the residual strength parameters of the material are essentially equal to its peak strength parameters, hence the term ideal/perfect. While the latter more realistic approximation states that the residual strength parameters are equal to depreciated values of the peak strength parameters.
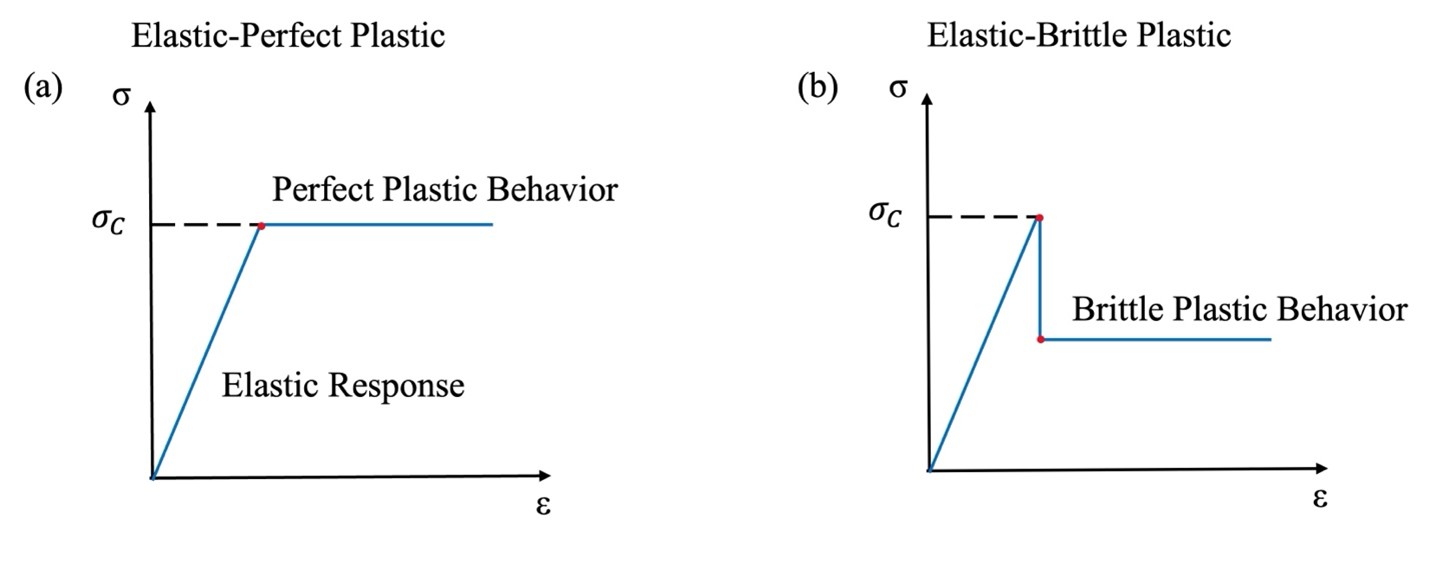
Fig. 3. Different post-yield responses of a material, specifically (a) perfect/ideal plastic; (b) brittle plastic (credit: Author).
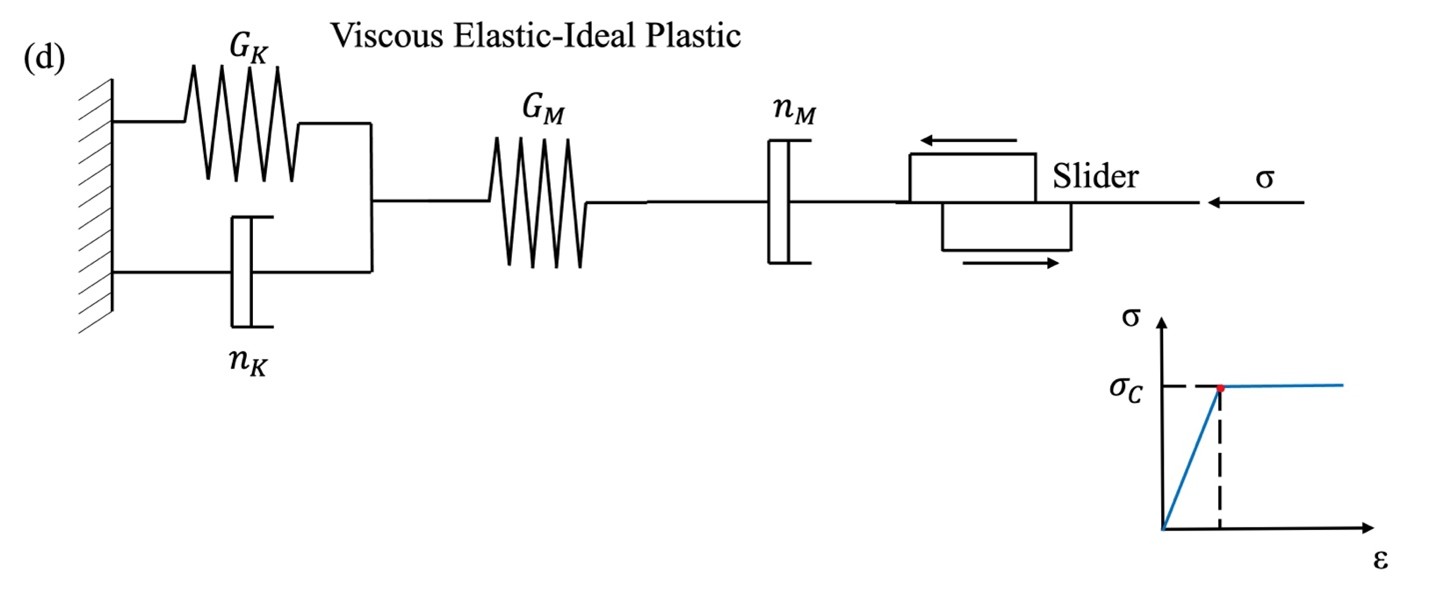
Now we can combine viscous, elastic, and plastic analogues to form a very simple viscous elastic-perfect plastic rheology (Fig. 4).
In the previous sentence the word simple is italicized to emphasize that this rheological behavior is considered somewhat elementary for applications in geodynamics, where more complicated creep models are applied to better simulate the response of viscous flowing rocks. In reality, the rheology of a rock is influenced by a many factors, including mineralogy, grain sizes, stress state, temperature and pressure conditions, whose effects cannot be easily determined. Consequently, simple linear rheological models, such as the ones that were briefly mentioned in the previous paragraphs, cannot adequately represent the behavior of solid Earth bodies such as the mantle or the subducting plates (Elbeshausen and Melosh 2020). The deformation mechanisms that better describe these features are diffusion creep, dislocation creep, and Peierls mechanism creep.
Simulating geodynamic-scale deformation with more realistic creep mechanisms
Diffusion creep is more likely to occur at low stress states and is mostly attributed to the diffusion of atoms in the crystal lattice. As a result, this type of deformation can take place either along the interior of the crystal grains (Herring-Nabarro creep) or along the boundaries of the grains (Coble creep), ultimately producing purely ductile behavior. This type of creep deformation is expressed by a linear/Newtonian relation between the strain rate and the stress. The two previous parameters are connected via a coefficient, or the so called ‘factor’, which heavily depends on the temperature, and the pressure (note: some researchers spend their entire scientific careers determining its value!).
The full expressions and an analytical discussion for the Herring-Nabarro and the Coble diffusion creep can be found in the esteemed book of Turcotte and Schubert (2002). Diffusion creep has been utilized in many notable geodynamic studies (e.g., Billen and Hirth 2005; Garel et al. 2014; Pusok and Kaus 2015; Pusok et al. 2018; Behr et al. 2022; Hummel et al. 2024).
Dislocation creep (often referred to as power-law creep) usually appears in high stress regimes due to displacements of dislocations inside the crystal lattice, and it’s an effective mechanism in the lithosphere. In contrast to the previous creep mode, the dislocation creep model is governed by a non-Newtonian (i.e., non-linear) relation between the strain rate and the stress (Ranalli 1995). Likewise with the diffusion creep, the power-law creep is also highly temperature-dependent. Many noteworthy works have used the dislocation creep model (e.g., Schmalholz 2011; Pusok et al. 2018; Ioannidi et al. 2021; Patocka et al. 2024).
Finally, the Peierls creep mechanism is a special type of temperature-dependent dislocation creep that acts at extremely high stress states and generally low temperatures. This creep deformation mechanism is thermally triggered by the detachment of dislocations that are forced away from their least-energy positions, due to intense applied stresses. The activation, and subsequent domination of the Peierls creep as the main creep mechanism is material dependent, with some materials being more susceptible than others. For instance, olivine is far more vulnerable in comparison to plagioclase. Overall, it can be safely assumed that it is usually activated for stresses above 0.1 GPa (Gerya 2010).
In addition, the Peierls creep mechanism can start at stresses much lower than the peak strength of the material, a property that other creep models do not possess. Therefore, it limits the strength of the rock when the latter is subjected to high stress fields.
Generally, the Peierls creep mechanism is especially important in various subduction processes, such as the realistic modelling of the deformation of slabs that have lower temperatures and higher stresses than the surrounding mantle (Gerya 2010). Similarly with the two previous creep mechanisms, the Peierls creep has been extensively utilized by researchers (e.g., Kameyama et al. 1999; Babeyko and Sobolev 2008; Duretz et al. 2011; Bessat et al. 2020; Auzemery et al. 2020).
In the majority of the previously cited studies of this section, a combination of all the three aforesaid creep deformation mechanisms was utilized, in order to better capture the complicated behavior of the geodynamic phenomena. A broader rheological relation can also be used, also known as the flow rule, which depending on the values that are chosen for certain coefficients, can account for either one of the three previously mentioned creep deformation mechanisms (Turcotte and Schubert 2002; Gerya 2010).
Wrap-up
My aim here was to offer a friendly introduction on the very important topic of rock rheology, which plays a central role in Geodynamics. What you’ve read here is only the ‘tip of the iceberg’, but I’ve made an attempt to include books and papers references, so that the reader may commence his ‘journey’ in the very fascinating and interdisciplinary field of rock rheology. To really get into the nitty-gritty of rock rheology, one must have a very vigorous understanding of the mathematical theory of elasticity and plasticity. If you’re up for the challenge, I recommend you two classical books on the theory of elasticity (Muskhelishvilli 1954; Timoshenko and Goodier 1970), and one for the theory of plasticity (Hill 1950).
References Jaeger JC, Cook NGW, Zimmerman RW (2007) Fundamentals of rock mechanics. 4th edition. Blackwel, USA. 10.1017/CBO9780511735349 Gerya T (2010) Introduction to Numerical Geodynamic Modelling. 1st edition. Cambridge University Press, Cambridge. https://doi.org/10.1017/9781316534243 Ranalli G (1995) Rheology of the Earth. 2nd edition. Springer Dordrecht. Kaus BJP, Becker TW (2007) Effects of elasticity on the Rayleigh-Taylor instability: implications for large scale geodynamics. Geophysical Journal International 168(2): 843-862. https://doi.org/10.1111/j.1365-246X.2006.03201.x Burov EB, Molnar P (2008) Small and large-amplitude gravitational instability of an elastically compressive viscoelastic Maxwell solid overlying an inviscid incompressible fluid: Dependence of growth rates on wave number and elastic constants at low Deborah numbers. Earth and Planetary Science Letters 275(3-4): 370-381. https://doi.org/10.1016/j.epsl.2008.08.032 Poliakov ANB, Cundall PA, Podladchikov YY, Lyakhovsky VA (1993) An Explicit Inertial Method for the Simulation of Viscoelastic Flow: An Evaluation of Elastic Effects on Diapiric Flow in Two- and Three- Layers Models. In: Stone, D.B., Runcorn, S.K. (eds) Flow and Creep in the Solar System: Observations, Modeling and Theory. NATO ASI Series 391: 175-195. Springer, Dordrecht. https://doi.org/10.1007/978-94-015-8206-3_12 Brady BHG, Brown ET (2006) Rock Mechanics for underground mining. 3rd edition. Springer Dordrecht. https://doi.org/10.1007/978-1-4020-2116-9 Elbeshausen D, Melosh HJ (2020) A nonlinear and time-dependent visco-elastic-plastic rheology model for studying shock-physics phenomena. Engineering Reports 2(12): 1-16. https://doi.org/10.1002/eng2.12322 Turcotte DL, Schubert G (2002) Geodynamics. 2nd edition, Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511843877 Garel F, Goes S, Davies DR, Davies JH, Kramer SC, Wilson CR (2014) Interaction of subducted slabs with the mantle transition-zone: A regime diagram from 2-D thermo-mechanical models with a mobile trench and an overriding plate. Geochemistry, Geophysics, Geosystem 15(5): 1739-1765. https://doi.org/10.1002/2014GC005257 Billen MI, Hirth G (2005) Newtonian versus non-Newtonian upper mantle viscosity: Implications for subduction initiation. Geophysical Research Letters 32(19): 1-4. https://doi.org/10.1029/2005GL023457 Behr WM, Holt AF, Thorsten BW, Faccenna C (2022) The effects of plate interface rheology on subduction kinematics and dynamics. Geophysical Journal International 230(2): 796-812. https://doi.org/10.1093/gji/ggac075 Hummel N, Buiter S, Erdos Z (2024) The influence of viscous slab rheology on numerical models of subduction. Solid Earth 15(5): 567-587. https://doi.org/10.5194/se-15-567-2024 Pusok AE, Kaus BJP (2015) Development of topography in 3-D continental-collision models. Geochemistry, Geophysics, Geosystems 16(5): 1378-1400. https://doi.org/10.1002/2015GC005732 Pusok AE, Kaus BJP, Popov AA (2018) The effect of rheological approximations in 3-D numerical simulations of subduction and collision. Tectonophysics 746: 296-311. https://doi.org/10.1016/j.tecto.2018.04.017 Schmalholz SM (2011) A simple analytical solution for slab detachment. Earth and Planetary Science Letters 304(1-2): 45-54. https://doi.org/10.1016/j.epsl.2011.01.011 Patocka V, Cizkova H, Pokorny J (2024) Dynamic Components of the Asthenosphere: Lateral Viscosity Variations Due To Dislocation Creep at the Base of Oceanic Plates. Geophysical Research Letters 51(13): 1-14. https://doi.org/10.1029/2024GL109116 Ioannidi PI, Pourhiet LL, Agard P, Angiboust S, Oncken O (2021) Effective rheology of a two-phase subduction shear zone: Insights from numerical simple shear experiments and implications for subduction zone interfaces. Earth and Planetary Science Letters 566: 116913. https://doi.org/10.1016/j.epsl.2021.116913 Kameyama M, Yuen DA, Karato SI (1999) Thermal-mechanical effects of low-temperature plasticity (the Peierls mechanism) on the deformation of a viscoelastic shear zone. Earth and Planetary Science Letters 168(1-2): 159-172. https://doi.org/10.1016/S0012-821X(99)00040-0 Bessat A, Duretz T, Hetenyi G, Pilet S, Schmalholz SM (2020) Stress and deformation mechanisms at a subduction zone: insights from 2-D thermomechanical numerical modelling. Geophysical Journal International 221(3): 1605-1625. https://doi.org/10.1093/gji/ggaa092 Auzemery A, Willingshofer E, Yamato P, Duretz T, Sokoutis D (2020) Strain localization mechanisms for subduction initiation at passive margins. Global and Planetary Change 195: 103323. https://doi.org/10.1016/j.gloplacha.2020.103323 Babeyko AY, Sobolev SV (2008) High-resolution numerical modeling of stress distribution in visco-elasto-plastic subducting slabs. Lithos 103(1-2): 205-216. https://doi.org/10.1016/j.lithos.2007.09.015 Duretz T, Gerya TV, May DA (2011) Numerical modelling of spontaneous slab breakoff and subsequent topographic response. Tectonophysics 502(1-2): 244-256. https://doi.org/10.1016/j.tecto.2010.05.024 Muskhelishvili NI (1954) Some basic problems of the mathematical theory of elasticity. 4th corrected and augmented edition. Springer Dordrecht. https://doi.org/10.1007/978-94-017-3034-1 Timoshenko SP, Goodier JN (1970) Theory of Elasticity. 3rd edition. Engineering Societies Monographs. McGraw-Hill Book Company. Hill R (1950) The mathematical theory of plasticity. 1st edition. Oxford University Press, Oxford. https://doi.org/10.1093/oso/9780198503675.001.0001