Shi Joyce Sim from School of Earth and Atmospheric Science, Georgia Institute of Technology.
Figure 1: Examples of two-phase flow in geodynamics
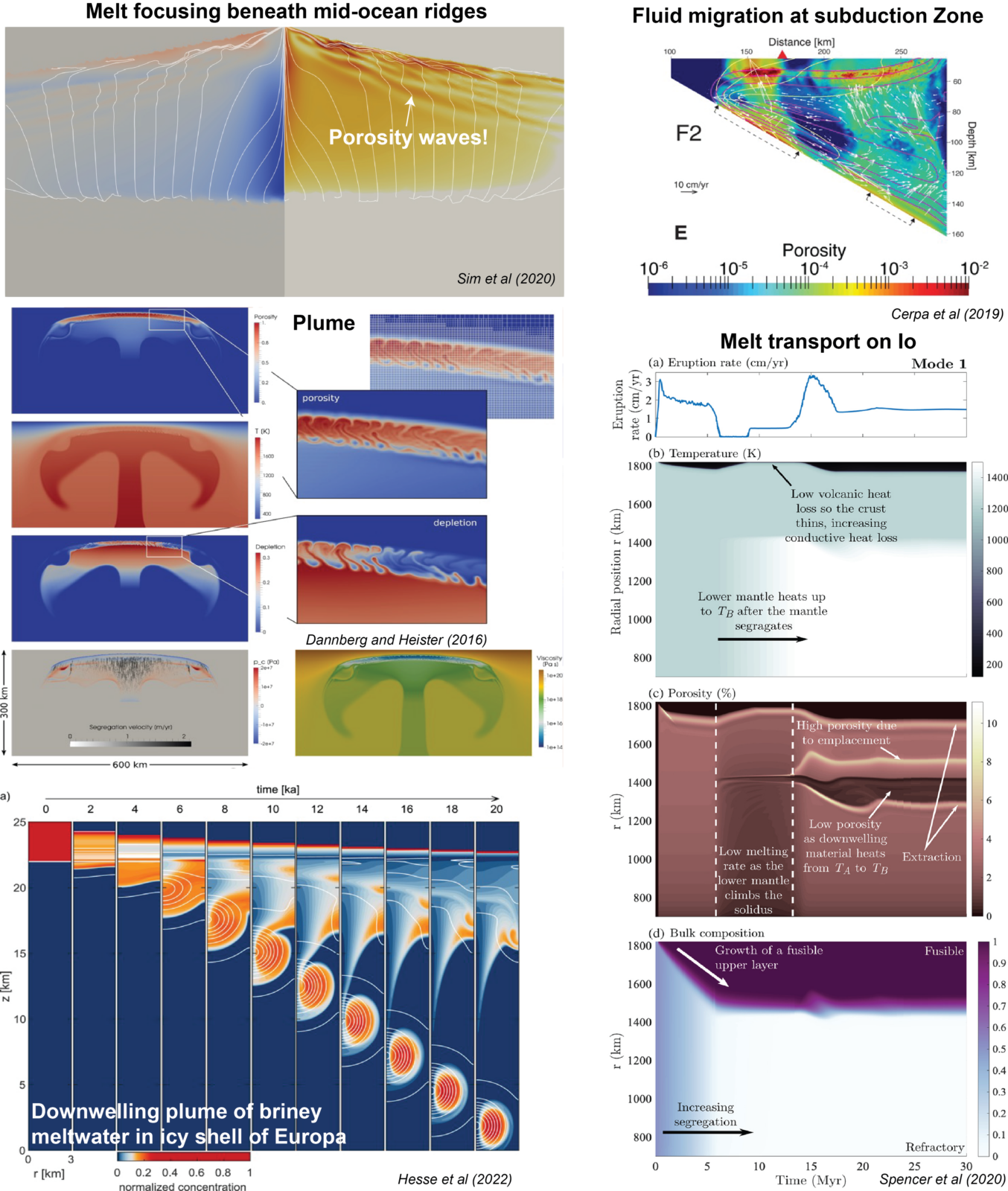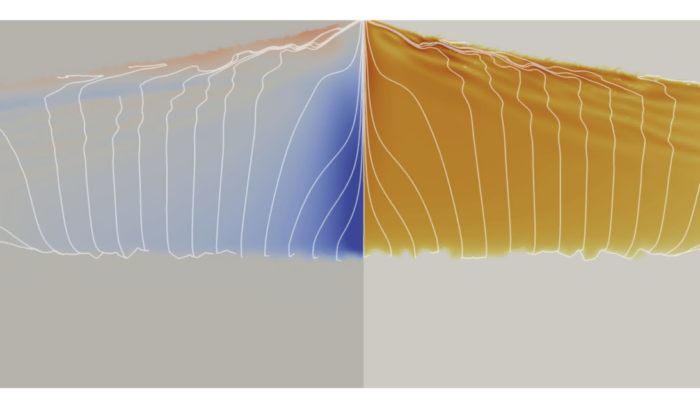
Now that you have a basic idea about two phase flow, you can begin to ask: does your science problem involve a fluid/liquid in a compactible matrix? Next, consider the fluid/liquid and matrix. Given the beginnings of the two-phase flow approach, silicate melt is the typical liquid in a peridotite matrix. Others include iron-sulfide melt in the lower mantle for forming the core or melt-water in an icy matrix, such as on Europa. Perhaps you have other exotic settings in mind too. Then, you will have to understand the dihedral angles that the liquid makes in the matrix grains, at least at equilibrium (disequilibrium textures require further exploration). Are the dihedral angles small enough for the liquid to be interconnected? Silicate melts typically have low dihedral angles in the upper mantle, i.e., the melt is interconnected even at low melt fraction. For materials with larger dihedral angles, such as iron-sulfide, you need to have a critical melt fraction to get interconnected Darcian-like flow, but by then you might have enough melt to get droplets of the liquid, thus making two-phase flow inapplicable. Another interesting setting is melt-water transport in an icy matrix, which is opposite in density, but more on density/buoyancy later.
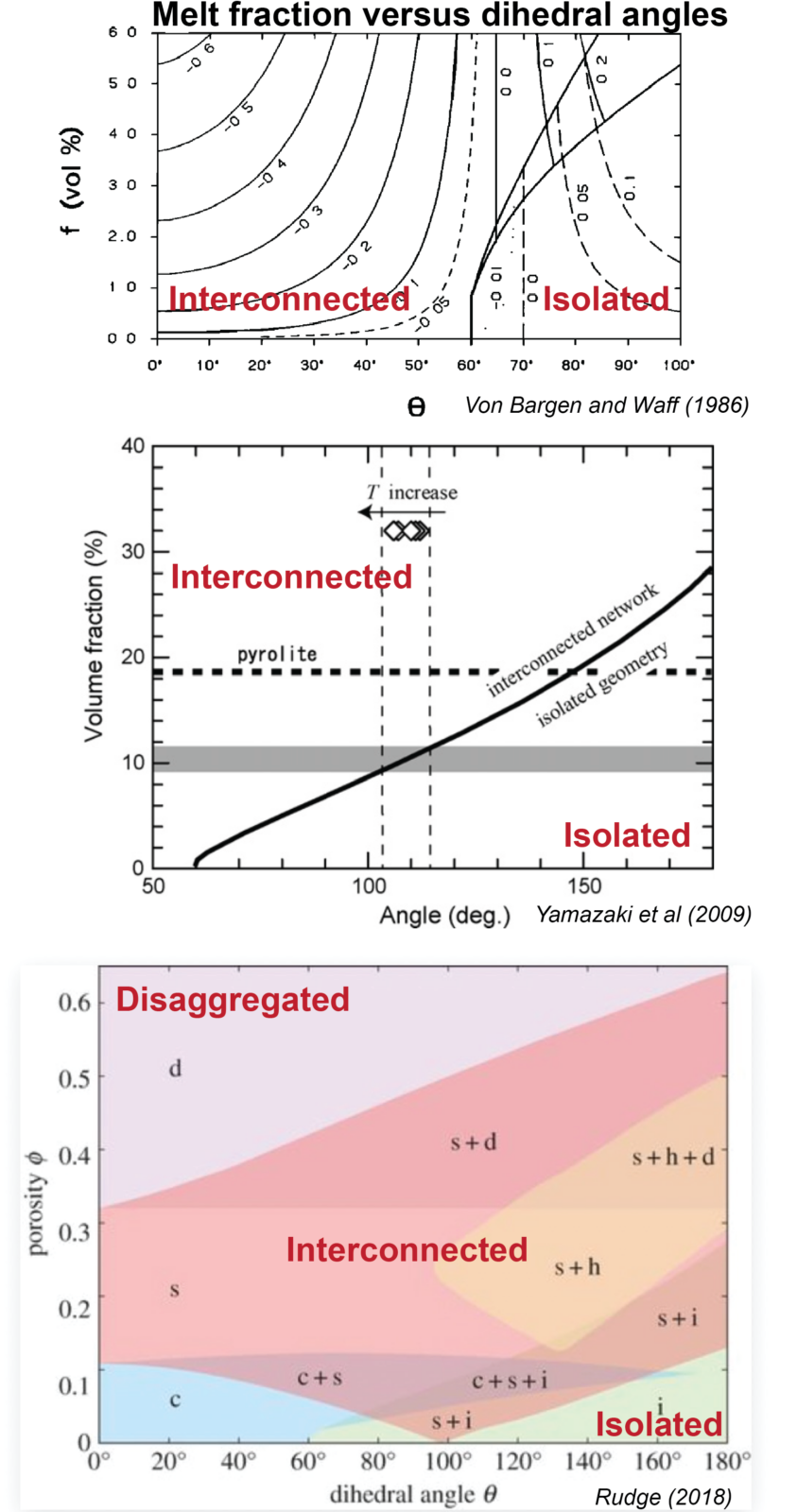
Dihedral angles depend on melt fraction, composition (major elements like iron, volatiles etc.), grain size, depth, anisotropy (deformation in the bulk), temperature, equilibrium/disequilibrium etc. Typically, dihedral angles increase with depth/pressure, so the fluid becomes more interconnected with increasing depth and the same amount of melt. For iron-sulfide melts, increasing both sulfur content and oxygen fugacity leads to a decrease in dihedral angles (Terasaki et al., 2005). This constitutes a part of the debate on core formation and the existence of magma ocean, i.e., if iron-sulfide melts can percolate through the lower mantle to form the core, a magma ocean phase does not need to be invoked (Roberts et al., 2007). The point is that you need to understand the relationship between the melt fraction/porosity versus dihedral angles (Figure 2) and the dihedral angles of your fluid/matrix combination in order to apply two-phase flow appropriately. Then, it comes down to parameterizing permeability for your choice of melt. Rudge, 2018 not only does a great job theoretically laying out the porosity and dihedral angle relationship but also sums up the parameterization of permeabilities nicely. The Kozeny-Carman relation is typically used for the permeability-porosity relation: K ~ d2pn/c, where d is the grain size, p is the porosity, n is an exponent on porosity, and c is the geometric factor. For silicate melts, n ~ 2.6 (Miller et al., 2014). Numerical models for melt transport tend to use either n = 2 or 3.
Figure 2: Experimental and theoretical works on dihedral angles.
Now that we have established the interconnectedness of the liquid at small melt fractions, we have to look at the other end of the limit: the disaggregation limit, where flow becomes suspended beyond the critical liquid fraction. Again, this depends on the liquid and matrix. For silicate melt, the limit is around 25-30 % (Hier-Majumder et al., 2006). Of course, this might change with depths and other parameters as well. There is also a rheological limit, as shown experimentally, to be between 25 to 30 % for silicate melt (Scott and Kohlstedt, 2006). Stocker and Gordon, 1975 also showed that the crystalline grains will remain in mechanical contact with each other at the intergranular faces if melt fractions are less than approximately 22%. The point is that, beyond these limits, the crystalline grains are no longer coupled mechanically and you step into the realm of suspended flow, which is governed by different physics compared to two-phase flow. Perhaps it would be more convincing to compare the difference between suspension flow and two-phase flow close to this limit or attempt to blend them together as this paper did (Wong and Keller, 2022). If anyone from the suspension flow community is interested in a fun collaboration, reach out!
The other aspect of two-phase flow melt is buoyancy. The melt tends to be more buoyant than the matrix from which it has melted. This is true for many settings that we are familiar with, i.e., magma is typically more buoyant than the surrounding materials in the upper mantle. The oddballs are magma at depths and iron-sulfide melts. There is another familiar material that is counter-intuitive and that is H2O! We all know ice cubes float in water. Given that the dihedral angles of meltwater in ice is smaller than 60°, you have interconnected flow, but water flows downwards! This is true for most melt water flows in icy shell on ocean worlds such as Europa, Enceladus, Ganymede and a few have applied two-phase flow approach to understand these transports (Hesse et al., 2020, Kalousova et al., 2014). This density inversion works because we are in a matrix of Ice-I, which is the typical everyday ice that we know and love. If we are in the realm of ice-III or higher, the density of water becomes less than that of the ice, so melt-water flows up.
The formulation for two-phase is inherently hard to solve, given all the coupling involved (permeability, bulk and shear viscosities all have relations with porosity, etc.). A simplification that can be made is to make an approximation in the limit of small porosity, where the set of equations becomes one way coupled such that the solid matrix does not feel the melt, i.e., buoyancy effects from melts are insignificant compared to bulk motion (Sim et al., 2020). This is only valid at low melt fractions perhaps up to the disaggregation limit (Spiegelman, 1993). There are many good works on different assumptions one can make and how to solve two-phase flow problems, but that is a topic for another day.
Two-phase or not two-phase, that is the question. I hope this is useful in helping you think about your problem and work out whether you can apply two-phase flow.
References: Hier-Majumder, S., Ricard, Y., & Bercovici, D. (2006). Role of grain boundaries in magma migration and storage. Earth and Planetary Science Letters, 248(3-4), 735-749. McKenzie, D. (1985). The extraction of magma from the crust and mantle. Earth and Planetary Science Letters, 74(1), 81-91. McKenzie, D. (1989). Some remarks on the movement of small melt fractions in the mantle. Earth and planetary science letters, 95(1-2), 53-72. Miller, K. J., Zhu, W. L., Montési, L. G., & Gaetani, G. A. (2014). Experimental quantification of permeability of partially molten mantle rock. Earth and Planetary Science Letters, 388, 273-282. Riley Jr, G. N., & Kohlstedt, D. L. (1991). Kinetics of melt migration in upper mantle-type rocks. Earth and Planetary Science Letters, 105(4), 500-521. Roberts, J. J., Kinney, J. H., Siebert, J., & Ryerson, F. J. (2007). Fe‐Ni‐S melt permeability in olivine: Implications for planetary core formation. Geophysical Research Letters, 34(14). Rudge, J. F. (2018). Textural equilibrium melt geometries around tetrakaidecahedral grains. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 474(2212), 20170639. Scott, D. R., & Stevenson, D. J. (1986). Magma ascent by porous flow. Journal of Geophysical Research: Solid Earth, 91(B9), 9283-9296. Scott, T., & Kohlstedt, D. L. (2006). The effect of large melt fraction on the deformation behavior of peridotite. Earth and Planetary Science Letters, 246(3-4), 177-187. Sim, S. J., Spiegelman, M., Stegman, D. R., & Wilson, C. (2020). The influence of spreading rate and permeability on melt focusing beneath mid-ocean ridges. Physics of the Earth and Planetary Interiors, 304, 106486. Sleep, N. H. (1974). Segregation of magma from a mostly crystalline mush. Geological Society of America Bulletin, 85(8), 1225-1232. Spiegelman, M. (1993). Physics of melt extraction: Theory, implications and applications. Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences, 342(1663), 23-41. Stocker, R. L., & Gordon, R. B. (1975). Velocity and internal friction in partial melts. Journal of Geophysical Research, 80(35), 4828-4836. Terasaki, H., Frost, D. J., Rubie, D. C., & Langenhorst, F. (2005). The effect of oxygen and sulphur on the dihedral angle between Fe–O–S melt and silicate minerals at high pressure: implications for Martian core formation. Earth and Planetary Science Letters, 232(3-4), 379-392. von Bargen, N., & Waff, H. S. (1986). Permeabilities, interfacial areas and curvatures of partially molten systems: results of numerical computations of equilibrium microstructures. Journal of Geophysical Research: Solid Earth, 91(B9), 9261-9276.
