Nonlinear Processes in Geosciences

NP Campfire: “Perspectives on Climate Science: from historical developments to research frontiers”

Tommaso Alberti January 19, 2021

Recently, the European Geosciences Union (EGU) started to support a new type of event called ‘Campfires’ that will give the Divisions the freedom to run online interactive events in a way that suits their needs. This allows the EGU Divisions to encourage interactions in their research communities through virtual informal meetings. In this framework, and thanks to a group of young and established s ...[Read More]

Perspectives on Climate Science: from historical developments to research frontiers

Tommaso Alberti October 5, 2020

Breaking news: a bizarre early-September snowstorm dumped snow from Montana to New Mexico, a medicane hit Southern Italian regions and Greece, heatwaves and droughts are expected to increase in the future… These extreme events are becoming more and more frequent and one question spontaneously arises: is climate change making the weather more extreme? This is one of the reasons why climate change i ...[Read More]

NPG Paper of the Month: “Application of a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems”

Tommaso Alberti April 23, 2020

Local dynamical properties of a segment of an example run for the coupled Lorenz system. (a) Alignment of directions of error growth plotted along the x coordinate of the ocean subsystem. Large orange stars indicate high alignment of error growth in the unstable or neutral subspaces. (b) Finite-time Lyapunov exponents (FTLEs) computed over window τ = 4. (c) Local Kaplan-Yorke dimension calculated from FTLEs. (Source: Quinn, O’Kane, and Kitsios, Application of a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems, Nonlin. Processes Geophys., 27, 51–74, 2020, https://www.nonlin-processes-geophys.net/27/51/2020/. License: https://creativecommons.org/licenses/by-nc-nd/4.0/.

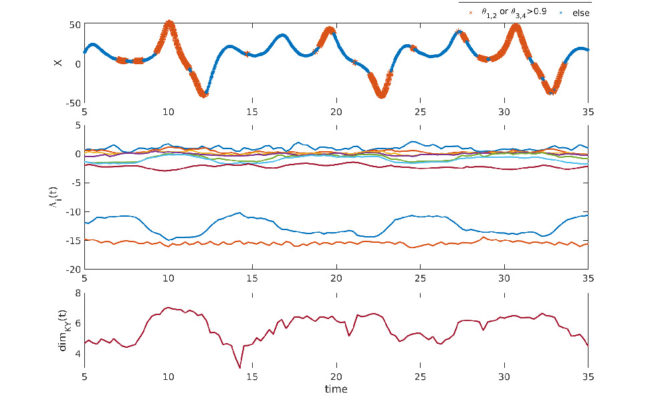
This month the NPG Paper of the Month award is achieved by Courtney Quinn for her paper “Application of a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems” (https://www.nonlin-processes-geophys.net/27/51/2020/). Dr. Courtney obtained her PhD in Mathematics at the University of Exeter (UK) researching critical transitions in dynamical syst ...[Read More]