This month the NPG Paper of the Month award is achieved by Courtney Quinn for her paper “Application of a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems” (https://www.nonlin-processes-geophys.net/27/51/2020/).
Dr. Courtney obtained her PhD in Mathematics at the University of Exeter (UK) researching critical transitions in dynamical systems. She is currently a member of the Decadal Climate Forecasting Project in the Oceans and Atmosphere business unit of CSIRO (Australia). Her current research involves applying nonautonomous dynamical systems analysis to various dimension reduction methods used in climate modelling.
The complexity of coupled Earth system models used for research and forecasting continues to increase by coupling between additional realms (or domains), including the land, ocean, atmosphere, sea-ice, and biogeochemical effects. A fundamental challenge of using these models lies in understanding how the respective domains of disparate spatio-temporal scales covary and influence each other. In the context of state estimation, strongly coupled data assimilation (CDA) in multiscale systems allows the quantification of such dynamics through the cross-domain covariances. However, due to computational limitations, it remains a challenge to accurately represent the covariances between these highdimensional coupled subsystems, where often one or more subsystems are unobserved. In the study presented in Quinn, O’Kane, and Kitsios (https://www.nonlin-processes-geophys.net/27/51/2020/), the authors explore the challenges of strong CDA through a conceptual multiscale chaotic model consisting of three coupled Lorenz attractors whose dynamics loosely emulates the interactions between the ocean, tropical atmosphere, and extratropical atmosphere.
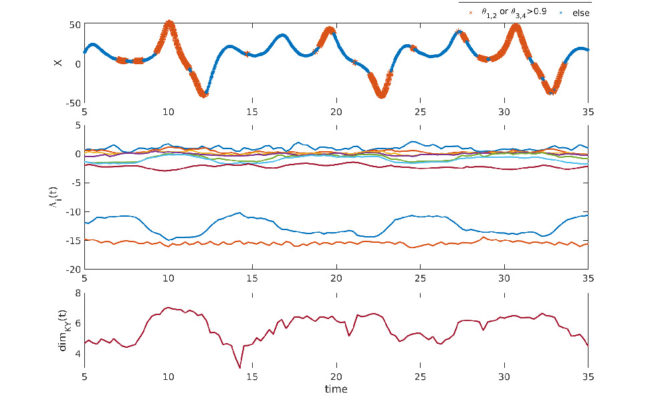
Using variants of the ensemble Kalman filter and conducting a comprehensive set of experiments assimilating sparse and or temporally correlated observations, they analyse the ability to track the nonlinear trajectory of each subsystem relying only on the cross-domain covariance to determine an accurate analysis increment (i.e. model state correction) for the unobserved subdomain. In particular, they explore a novel method of defining the rank of the background covariance matrix (equivalently the number of ensemble methods) at each analysis step by a measure of the local (time dependent) attractor dimension (i.e., the Kaplan–Yorke dimension) calculated from finite-time Lyapunov exponents (FTLEs) which measure the time dependent rates of growth and decay. This approach defines the minimal rank while the retained covariant Lyapunov vectors (CLVs) span all critical local directions of error growth. The authors experiment with a variety of observational sets, including leaving some subsystems completely unobserved, and different types of observational error (correlated and uncorrelated). They show that the local dimension approach performs closest to the full-rank method compared to other reduced-rank methods where the rank is determined a priori. For correlated observation errors, the variable dimension CLV approach out-performs all other approaches, including full-rank. Where weak coupling between subsystems leads to covariance collapse in one or more of the unobserved subsystems, the authors also propose a novel scaling of the Kalman gain which increases the magnitude of the innovations and the effective dimension of the unobserved domains relative to the strength of the coupling and timescale separation. Overall, the study provides an initial understanding of the dynamics associated with strong CDA in multiscale nonlinear systems such as those involved in weather and climate prediction.