The January 2021 NPG Paper of the Month award goes to Olivier Pannekoucke and his co-authors for the paper “A methodology to obtain model-error covariances due to the discretization scheme from the parametric Kalman filter perspective“.
In geophysics, forecasting is based on solving the equations of physics with the help of a computer. To calculate a forecast we need an initial condition. Estimating this condition is difficult, however, because in general the observations available are few or heterogeneously distributed in space and time. To achieve this, a reference algorithm is given by the Kalman filter. This algorithm is based on temporal propagation during the prediction stage; and the updating of the prediction and analysis error covariance matrices during the analysis stage.
While the formalism of the Kalman filter is based on simple formulas of linear algebra, its practical implementation faces two pitfalls :
Indeed, in the systems of interest to us, these matrices are very large and it is impossible to compute their temporal propagation during forecasting. The ensemble Kalman filter, by approximating the covariance matrices by an ensemble estimation, offers a way to propagate the covariances from the forecast of each member of the ensemble.
Secondly, while part of the forecast error statistics can be explained by the propagation of initial uncertainties – the predictability error – , another contribution, linked to the defect in the numerical model – the model error – is much more difficult to characterize. To go further in understanding model error, the working hypothesis of a decorrelation between the predictability error and the model error is often introduced, which then leads to decompose the prediction error covariance matrix as the sum of the predictability error and model error covariance matrices. Despite this assumption it is very difficult to characterize the model error statistics, and moreover the predictability error is never decorrelated from the model error.
The objective of the paper is to characterize the model-error covariances related to the discretization of physics equations, i.e. the errors that emerge during the transition from the mathematical formalism of physics equations to their implementation on a computer and then to their numerical resolution. To achieve this, we relied on a new method: the parametric Kalman filter (PKF). The PKF is an implementation of the Kalman filter, in which covariance matrix are approximated by a covariance model characterized by a set of parameters (Pannekoucke et al. , 2016; Pannekoucke et al. 2018). Thus, by describing how the parameters evolve over time, we can describe, in an approximate way, the evolution of the full covariance matrix.
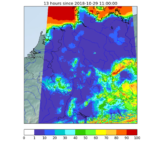
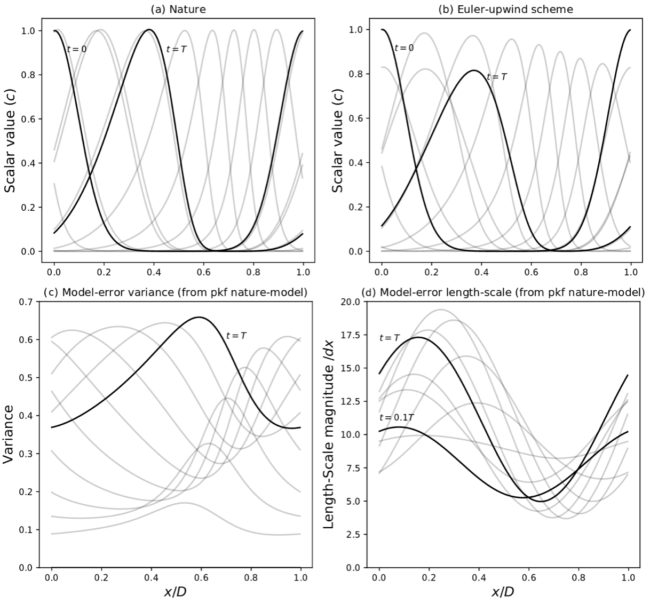
By revisiting the formalism of the model-error covariance matrix and using the PKF, we have characterised one of the observed defects in the prediction of the chemical composition of the atmosphere where it appeared that the variances of the forecast error estimated by an ensemble decrease abnormally with time, a phenomenon called the loss of variance. We have shown that this loss of variance is related to a diffusive effect – the origin of which appears when determining the modified equation which is the differential equation whose solution is the numerical prediction – as shown in Figure 1. The panel (a) shows the real evolution of the concentration of a chemical compound transported by a heterogeneous wind and (b) the numerical prediction calculated from a simple numerical scheme: it is observed that the intensity of the numerical solution decreases abnormally compared to the theoretical solution. With the PKF equations, we have characterized the evolution of the model error variance (panel c), which we have shown to be coupled with the evolution of the anisotropy of the correlation functions (characterized by the significant correlation scale, panel d). This is the first time that we have been able to characterize the properties of the model error covariance matrix linked to the defects of the numerical resolution scheme.
This article has not only enabled us to understand a behaviour observed in practice (here the loss of variance), but above all it has opened up a new theoretical avenue of exploration for the characterization of model error covariances.
References
O. Pannekoucke, S. Ricci, S. Barthelemy, R. Ménard, and O. Thual, “Parametric Kalman Filter for chemical transport model,” Tellus, vol. 68, p. 31547, 2016, doi: 10.3402/tellusa.v68.31547.
O. Pannekoucke, M. Bocquet, and R. Ménard, “Parametric covariance dynamics for the nonlinear diffusive Burgers’ equation,” Nonlinear Processes in Geophysics, vol. 2018, pp. 1–21, 2018, doi: https://doi.org/10.5194/npg-2018-10.