The June 2020 NPG Paper of the Month award goes to Sebastian Lerch and colleagues for their paper “Simulation-based comparison of multivariate ensemble post-processing methods” (https://doi.org/10.5194/npg-27-349-2020).
Sebastian Lerch is a researcher at the Faculty of Mathematics of the Karlsruhe Institute Technology (KIT). He has a background in mathematics and statistics, his research interests include probabilistic forecasting, forecast evaluation, and the development of statistical and machine learning models for applications in the environmental sciences. The paper presented here is joint work with Sándor Baran (University of Debrecen), Annette Möller (Technical University of Clausthal), Jürgen Groß (University of Hildesheim), Roman Schefzik (German Cancer Research Center), Stephan Hemri (Federal Office of Meteorology and Climatology MeteoSwiss) and Maximiliane Graeter (KIT).
Most weather forecasts are based on ensemble simulations of numerical weather prediction models. Despite continued improvements, these ensemble predictions often exhibit systematic errors that require correction via statistical post-processing methods. Most post-processing methods utilize statistical and machine learning techniques to produce probabilistic forecasts in the form of full probability distributions of the quantity of interest. The focus usually is on univariate approaches where ensemble predictions for different locations, time steps and weather variables are treated independently. However, many practical applications of weather forecasts require one to accurately capture spatial, temporal, or inter-variable dependencies. Important examples include hydrological applications, air traffic management, and energy forecasting. Such dependencies are present in the physically consistent raw ensemble predictions but are lost if standard univariate post-processing methods are applied separately in each margin.
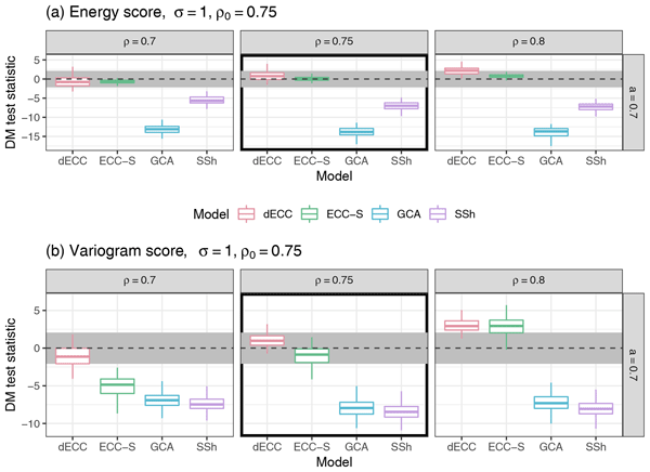
Over the past years, a variety of multivariate post-processing methods has been proposed. Most of these methods follow a two-step strategy. In a first step, univariate post-processing methods are applied independently in all dimensions, and samples are generated from the obtained probability distributions. In a second step, the multivariate dependencies are restored by re-arranging the univariate sample values with respect to the rank order structure of a specific multivariate dependence template. Popular established methods include ensemble copula coupling (ECC), where the dependence template is learned from the raw ensemble predictions, the Schaake shuffle (SSh), where the dependence template is learned from past observations, and the Gaussian copula approach (GCA), where a parametric dependence model is assumed. Over the past years, several extensions of those approaches, in particular of ECC, have been proposed, however, the literature lacks guidance on which approaches work best for which situations. Therefore, the overarching goal of our paper is to provide a systematic comparison of state-of-the-art methods for multivariate ensemble post-processing.
To achieve this, we propose three simulation settings which are tailored to mimic different situations and challenges that arise in applications of post-processing methods. In contrast to case studies based on real-world datasets, simulation studies allow one to specifically tailor the multivariate properties of the ensemble forecasts and observations and to readily interpret the effects of different types of misspecifications on the forecast performance of the various post-processing methods.
Overall, we find that the Schaake shuffle constitutes a powerful benchmark method that proves difficult to outperform, except for naive implementations in the presence of structural change (for example, time-varying correlation structures). Not surprisingly, variants of ensemble copula coupling typically perform the better the more informative the ensemble forecasts are about the true multivariate dependence structure. A particular advantage is the ability to account for flow-dependent differences in the multivariate dependence structure if those are (at least approximately) present in the ensemble predictions. Perhaps not surprisingly, the results generally depend on the simulation setup, and there is no consistently best method across all settings and potential misspecifications of the ensemble predictions. Nonetheless, the simulation studies offer some guidance, in particular on which of the ECC variants perform best for general types of misspecifications.
The computational costs of all presented methods are not only negligible in comparison to the generation of the raw ensemble forecasts, but also compared to the univariate post-processing as no numerical optimization is required. It may thus be generally advisable to compare multiple multivariate post-processing methods for the specific dataset and application at hand. An important aspect for future work will be to complement the comparison of multivariate post-processing methods by studies based on real-world datasets of ensemble forecasts and observations.