This month the NPG Paper of the Month award is achieved by Courtney Quinn for her paper “Application of a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems” (https://www.nonlin-processes-geophys.net/27/51/2020/). Dr. Courtney obtained her PhD in Mathematics at the University of Exeter (UK) researching critical transitions in dynamical syst ...[Read More]
NPG Paper of the Month: “Application of a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems”
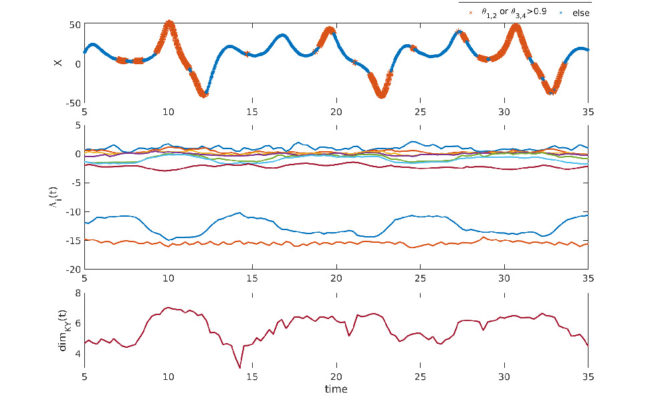
Local dynamical properties of a segment of an example run for
the coupled Lorenz system. (a) Alignment of directions of error growth plotted along the x coordinate of the ocean subsystem. Large orange stars indicate high alignment of error growth in the unstable or neutral subspaces. (b) Finite-time Lyapunov exponents (FTLEs) computed over window τ = 4. (c) Local Kaplan-Yorke dimension calculated from FTLEs. (Source: Quinn, O’Kane, and Kitsios, Application of
a local attractor dimension to reduced space strongly coupled data assimilation for chaotic multiscale systems, Nonlin. Processes Geophys., 27, 51–74,
2020, https://www.nonlin-processes-geophys.net/27/51/2020/. License: https://creativecommons.org/licenses/by-nc-nd/4.0/.
