As part of welcoming new members to the editorial team of Nonlinear Processes in Geophysics (NPG), we are pleased to present short interviews with two newly appointed editors, Dr. Kira Rehfeld and Dr. Jezabel Curbelo. They share their scientific backgrounds, motivations for joining the journal, editorial goals, and perspectives on emerging research directions in nonlinear geosciences. Their insigh ...[Read More]
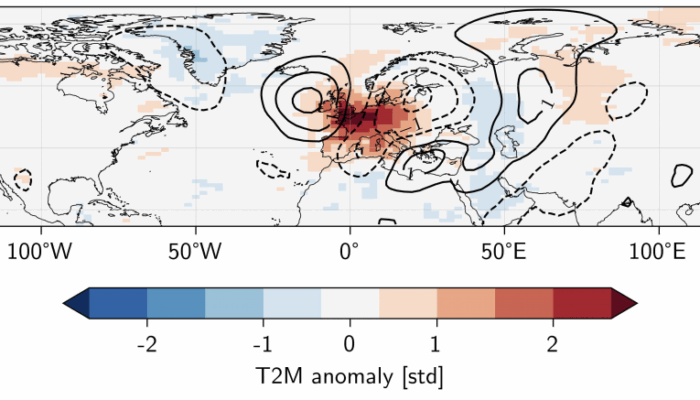
Extreme meteorological and climatological events can be immensely damaging and disruptive to society. Understanding the physical mechanisms driving these events, and how they will evolve with climate change is crucial for informing societal adaptation to our changing climate. However, extreme events are, by definition, rare. Our capacity to understand these events is, therefore, hindered by the sm ...[Read More]
From 1–5 August 2025, the medieval hilltop town of Erice, Sicily, hosted the second UNDERPIN workshop, a meeting organised within the Nonlinear Processes in Geosciences community and dedicated to advancing the science of weather extremes. The event brought together a truly diverse group of researchers, spanning climate dynamics, attribution science, socio-economic impacts, statistical physics, and ...[Read More]
The original goal of this study was to understand how the local dimension of the attractor of a dynamical system could be used to estimate the predictability of the future state of the system, and apply this in the case of radar images of rain. The local dimension using Extreme Value Theory (EVT) has been introduced and used in Faranda et al. (2017) to infer the current predictability of different ...[Read More]
