The NPG paper of the month was awarded to “Inferring the instability of a dynamical system from the skill of data assimilation exercises” by Yumeng Chen, Alberto Carrassi, and Valerio Lucarini.
Geophysical systems are usually described by a set of dynamical equations that are often non-linear and chaotic (Ghil and Lucarini, 2020). Errors about the initial state can grow, shrink, or stay constant with time, depending on error projections onto unstable, stable or neutral subspaces of the dynamical system. The properties of these subspaces can be measured by the Lyapunov exponents (Eckmann and Ruelle, 1985). Knowing the spectrum of Lyapunov exponents is thus immensely important as it can guide prediction strategies or inform decision making (Kalnay, 2003).
In particular, knowledge of the unstable modes can instruct the number of model realizations in an ensemble forecast system, or the deployment of efficient observation network. A notable example is the design of data assimilation (DA) that can be guided by the instability properties of the dynamical system assimilating data. Unfortunately, computing the Lyapunov exponents is extremely costly and computational burden grows quickly with the system’s dimension.
In Chen et al. (2021), we took the opposite viewpoint and showed that it is possible to use the output of DA to infer some fundamental properties of the spectrum of the Lyapunov exponents. Building upon previous studies (Bocquet et al., 2017; Bocquet and Carrassi, 2017), we derived a relation involving the error of DA, the size of the unstable-neutral subspace and the largest Lya- punov exponent.
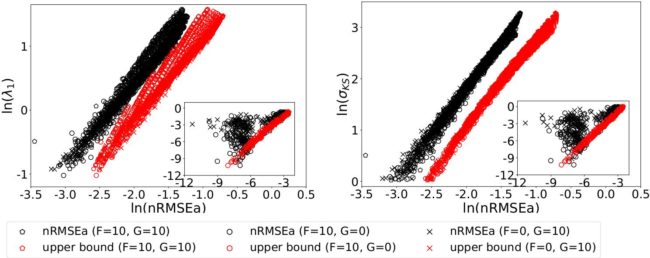
Our numerical analysis is based on the new Vissio and Lucarini (2020) model, an extension of the Lorenz (1996) system that is able to mimic the co-existence of wave-like and turbulent features in the atmosphere and the interplay between dynamical and thermodynamical variables, in such a way that the Lorenz (1955) energy cycle can be established. Our results demonstrate the robustness of the relation between the skill of DA and the instability property for varying model parameters, especially, as expected, under strong observational constraint. We also look at the Kolmogorov- Sinai entropy, estimated as the a sum of all positive Lyapunov exponents (Eckmann and Ruelle, 1985), which measures the rate at which information is lost, and relate it to the skill of DA. As shown in Figure 1, the first Lyapunov exponent and the Kolmogorov-Sinai entropy appears clearly linearly related to the RMSE of the analysis, as predicted by the theory. Deviations from the linear trend are seen in the weakly unstable cases (see Chen et al. (2021) for rationale of this behaviour).
From the linear relation, our approach implies an efficient way to infer the largest Lyapunov exponent and the Kolmogorov-Sinai entropy under varying model parameters. Although further investigation is needed for more complex scenarios, this study paves the path to exploring the sen- sitivity of model instability to model parameters even in complex, high-dimensional geophysical systems.
References
Bocquet, M. and Carrassi, A.: Four-dimensional ensemble variational data assimilation and the unstable subspace, Tellus A: Dynamic Meteorology and Oceanography, 69, 1304504, https://doi.org/10.1080/16000870.2017.1304504, 2017.
Bocquet, M., Gurumoorthy, K. S., Apte, A., Carrassi, A., Grudzien, C., and Jones, C. K. R. T.: Degenerate Kalman Filter Error Covariances and Their Convergence onto the Unsta- ble Subspace, SIAM/ASA Journal on Uncertainty Quantification, 5, 304–333, https://doi.org/ 10.1137/16M1068712, 2017.
Chen, Y., Carrassi, A., and Lucarini, V.: Inferring the instability of a dynamical system from the skill of data assimilation exercises, Nonlinear Processes in Geophysics, 28, 633–649, https://doi.org/10.5194/npg-28-633-2021, 2021.
Eckmann, J. P. and Ruelle, D.: Ergodic theory of chaos and strange attractors, Reviews of Modern Physics, 57, 617–656, 1985.
Ghil, M. and Lucarini, V.: The physics of climate variability and climate change, Rev. Mod. Phys., 92, 035 002, https://doi.org/10.1103/RevModPhys.92.035002, 2020.
Kalnay, E.: Atmospheric Modeling, Data Assimilation and Predictability, Cambridge University Press, Cambridge, 2003.
Lorenz, E.: Available potential energy and the maintenance of the general circulation, Tellus, 7, 157–167, 1955.
Lorenz, E. N.: Predictability – a problem partly solved, in: Predictability of Weather and Climate, edited by Palmer, T. and Hagedorn, R., pp. 40–58, Cambridge University Press, 1996.
Vissio, G. and Lucarini, V.: Mechanics and thermodynamics of a new minimal model of the atmo- sphere, EPJ Plus, 135, 807, https://doi.org/10.1140/epjp/s13360-020-00814-w, 2020.




