This month the NPG Paper of the Month award is achieved by Jonathan Deameyer and Stéphane Vannitsem for their paper “Correcting for model changes in statistical postprocessing – an approach based on response theory” (https://doi.org/10.5194/npg-27-307-2020).
Jonathan did his PhD in statistical mechanics at the Université Libre de Bruxelles under the supervision of Pierre Gaspard and he is currently working at the Royal Meteorological Institute of Belgium (RMIB) as a researcher. His current research activities concern the study and the application of statistical postprocessing to weather forecasts. In addition, the main focus of its unit’s research at RMIB is on the predictability and variability of geophysical systems.
Stéphane is the head of the Dynamical Meteorology and Climatology Unit of the Research division of the Royal Meteorological Institute of Belgium, and lecturer at the Free University of Brussels. He is currently president of the Nonlinear Processes division of the European Geosciences Union and executive editor of the journal “Nonlinear Processes in Geophysics”. His main research interests and expertise are oriented toward the application and adaptation of techniques of dynamical systems theory, chaos theory and stochastic processes to the study of atmospheric and climate dynamics with emphasis on their variability and predictability.
All models are wrong, or in other words, models are always approximations of reality. Weather forecast models are no exception to the rule. Their output is biased and this bias tends to increase over the lead time of the forecasts; as the models converge to their own climatology. Since the advent of modern weather forecasting, the forecasts issued by the weather prediction centers are thus corrected to lessen these biases, by using what is known as statistical postprocessing. In this framework, one of the most widely used technique consists in a linear regression between the database of the past forecasts and the database of observations, called Model Output Statistics (MOS).
For this method to be efficient, one needs a statistically homogeneous database of past forecasts. In short, the forecasts must have been produced by the same model to avoid internal biases inside the database. Alas, in order to improve the forecasts, weather forecast models goes through many cycles of modification. One way to conserve an homogeneous database of past forecasts is then to recompute all of them once a new model version is available. This effort is known as reforecasting and the past forecasts hence obtained are called reforecasts. Computing reforecasts is computationally costly, and for a weather prediction center, the decision to produce them or not may be a difficult one. As such, coping the impact of model changes on postprocessing schemes is a research topic with high priority in weather centers
In Correcting for model changes in statistical postprocessing – an approach based on response theory, we focus on a new approach to adapt the statistical postprocessing schemes to a new model. The idea is to use the information about the change between the old and the new model, assuming that it is an explicit change in the equations of the model, to compute the correction needed to adapt the postprocessing scheme of the old model. With the model change information, the perturbative theory known as Response theory developed for dynamical system allows to isolate the perturbation induced by the model change on the statistical moments used by the statistical postprocessing scheme and to obtain the new postprocessing scheme of the new model without relying on the reforecasts.
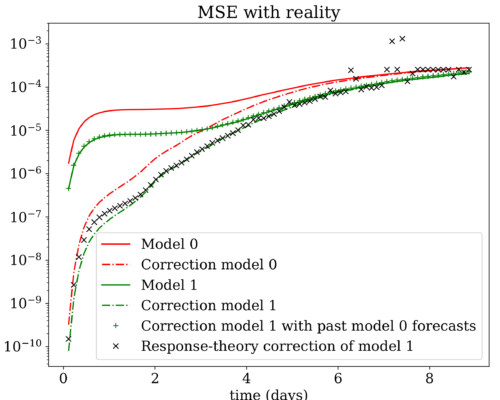
This approach is tested in the context of an idealized model of the mid-latitude synoptic-scale atmospheric variability (Reinhold and Pierrehumbert (1982)). The model changes considered are modifications of the model’s parameters such as the atmospheric internal friction or the intensity of the meridional temperature gradient. For instance, the impact of a change of the temperature gradient on the correction of an EVMOS postprocessing scheme – a variant of MOS – is shown on Figure 1. It shows the Mean Square Error (MSE) between the forecasts and the observations at successive lead times, the lower this error the better the forecasts. In red, the forecasts before the model change (Model 0), in green the forecasts after it (Model 1). The dash-dotted lines depicts the MSE of the forecasts corrected by the EVMOS trained with the forecasts of the corresponding model, i.e. Model 0 EVMOS is trained with Model 0 forecasts and Model 1 EVMOS is trained with Model 1 forecasts. We see that this scheme is efficient in reducing errors up to 3~4 days. The green crosses show what happen when Model 1 EVMOS is trained with the forecasts of Model 0, i.e. when a postprocessing scheme is trained with biased data. The benefit of using the EVMOS is lost, and the forecasts are not corrected. The MSE of the corrected forecasts using the postprocessing scheme computed with the response theory is depicted by black crosses and indicates that this method based on the model change information is efficient.
A question left open about the method by the present work is its comparative advantages/disadvantages with respect to the method based on reforecasts. It will depend on the computational cost of the tangent linear model used by the response theory versus the cost of the full non-linear model used to compute the reforecasts. This question will be adressed in the future.