Today’s our blog hosts a review article by the 2016 EGU Richardson medallist Peter Read, together with Daniel Kennedy, Neil Lewis, Hélène Scolan, Fachreddin Tabataba-Vakili, YixiongWang, Susie Wright, and Roland Young for the special issue of NPG celebrating 100 years of IUGG (https://npg.copernicus.org/articles/27/147/2020/npg-27-147-2020.html).
One of the great achievements of the past 100 years in fluid dynamics has been the development of a theory of dynamical instability, embracing both linear and nonlinear processes. In a geophysical context, this has led to a quantitative understanding of a variety of phenomena, including the processes that lead to the development of large-scale energetic eddies in rotating, stratified atmospheres and oceans. These instabilities, known as baroclinic and barotropic instabilities, are well known as the principal mechanisms responsible for the production of the dominant energy-containing eddies in the atmospheres of Earth and several other planets, as well as Earth’s oceans. In the article entitled above, Peter Read and his colleagues review our state of knowledge and understanding of these instabilities and their interactions with their wider environments, drawing on a range of sources that include laboratory experiments and various kinds of theoretical and numerical model, finally examining in some detail how they may manifest themselves in the diverse and varied atmospheres and oceans of our Solar System.
Early theoretical work on these instabilities focused on linearised problems, whose main purpose was to establish mathematical conditions under which a given flow might, or might not, become unstable. This led to the well known Rayleigh-Kuo and Charney-Stern-Pedlosky necessary, but insufficient, conditions for instability. But such studies could not accurately predict how the resulting instabilities would develop nonlinearly and equilibrate at later times, modifying the original large-scale flow through nonlinear feedbacks. In the modern era, therefore, focus has shifted more towards quantitative efforts to understand and predict the nonlinear equilibration processes and their implications for the long-term structure, energetics and transport properties of the flow. In particular, are there circumstances when barotropic or baroclinic instabilities may act as a self-organized criticality process, where the instability adjusts the flow towards a state of marginal instability or a related condition? And if so, how does this manifest itself in real systems, such as in laboratory experiments or in atmospheres and oceans?
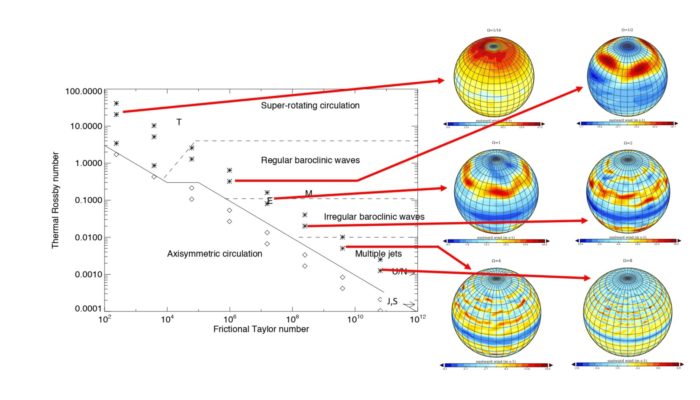
The answers to these questions turn out to be surprisingly rich and complex. For example, for slowly rotating planets (like Titan, or Venus – though the latter is even more complicated!) we tend to find (kinetic energy-dominated) barotropic shear instability dominating the atmospheric flow, whereas the atmospheres and oceans on more rapidly rotating planets (like Earth or Mars) are dominated by (potential energy-dominated) baroclinic instabilities. But for very rapidly rotating gas giant planets, the equilibrated zonal jet structure seems to be close in form to a barotropically marginally unstable state, as defined by a nonlinear stability criterion discovered by Vladimir Arnol’d that deserves to be more widely known. An unexpected by-product of this result turns out to lead to an indirect way of measuring the rotation period of the deep interiors of Jupiter and Saturn which, for Saturn, is difficult to determine by other means. In our article we show how this and many other insights can be obtained by exploring the variation in the structure and properties of equilibrated flows as certain critical dimensionless parameters are varied. This has long been the experience and practice of laboratory experimentalists, as we discuss in the article. But many such insights carry over to more realistic atmospheric or oceanic situations by treating a well formulated and generic numerical model like a laboratory experiment with a wide, multi-dimensional parameter space to explore. We are thereby gaining a broader perspective on almost all of the planets in our Solar System (and beyond!) as sibling members of a wider family of complex, nonlinear dynamical systems.