The February 2021 NPG Paper of the Month award goes David Wichmann and his co-authors for their paper “Ordering of trajectories reveals hierarchical finite-time coherent sets in Lagrangian particle data: detecting Agulhas rings in the South Atlantic Ocean“.
Understanding the transport of tracers and particulates is an important topic in oceanography and in fluid dynamics in general. The trajectory of an individual fluid parcel will in many cases strongly depend on its initial condition, i.e. the flow is chaotic. At the same time, on a more macroscopic level, many flows possess some form of structure that is less sensitive to the initial conditions of the individual parcels. This structure is determined by the collective behaviour of groups of parcels for intermediate or long times.
An example for such macroscopic structure in geophysical flows are eddies. In the ocean, mesoscale eddies (at the order of 10-100 km) are well-known for capturing water masses while being transported by a background flow. For describing the pathway of a fluid parcel that is captured in an eddy, what really matters is the motion of the entire eddy in the background flow, and not so much where exactly that parcel is within the eddy. We can simplify the problem by saying that all parcels in the eddy approximately go the same pathway, i.e. the particles stay approximately coherent over a certain time interval. Such sets of fluid parcels (or fluid volume) have therefore been termed “finite-time coherent sets” or “Lagrangian coherent structures” in the fluid dynamics community.
In our article, we explore a density-based clustering technique, the so called OPTICS algorithm (Ordering Points To Identify the Clustering Structure) published by Ankerst et. al in 1999, for the detection of such finite-time coherent sets. The goal of density-based clustering is simple: find groups of points that are densely distributed, i.e. those points that are all close to each other. We take modelled trajectories of fluid parcels and represent them as points in a high dimensional Euclidean space. In this way, two points in that space that are very close in terms of their Euclidean distance correspond to parcels that stay close to each other along their entire trajectory. Once this is done, OPTICS does the rest. In the form we propose, the method does not need any sophisticated pre-processing of the trajectory data. What’s also nice about OPTICS is that it is available in the scikit-learn library of Python, so it is quite straightforward to use.
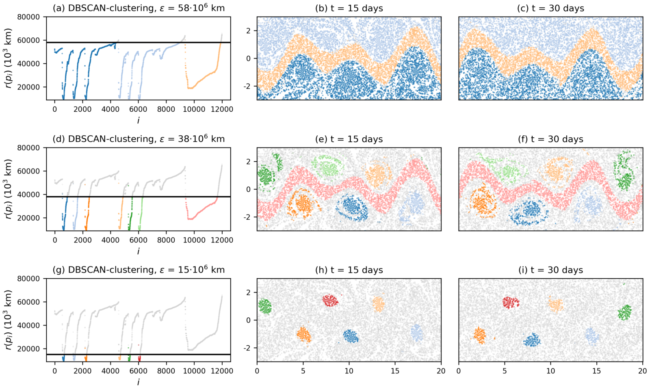
What OPTICS does is that it takes the data and creates a reachability plot. This is a quite condensed visualization of how similar fluid trajectories are – condensed because it is a one-dimensional graph defined on the trajectories. OPTICS creates an ordered list of the trajectories in such a way that densely populated regions are close to each other in this list. Finite-time coherent sets can then simply be identified by examining the “topography” of this plot, i.e. at the troughs and crests. An example for a reachability plot for a model flow containing an atmospheric jet and vortices, the Bickley Jet model flow, can be seen in the first column of the figure above. One can obtain clustering results by thresholding the reachability value (the y-axis of that plot) at a specific value , and then identify connected regions below the line as a coherent set. This method is also known as DBSCAN clustering, but what is special about OPTICS is that multiple DBSCAN clustering results (i.e. for different horizontal lines) can be obtained from one reachability plot.
Two things are special about OPTICS that make it specifically usable for the situations in fluid dynamics. First, it has an intrinsic notion of coherence hierarchies. We can see this by looking at the different rows in the figure, where the clustering result for different choices of are shown. For a large (first row in the figure), we really only see the very large-scale structure of the jet separating the northern and southern parts of the fluid. Decreasing is then similar to using a magnifying glass: if we look closer, we identify smaller individual eddies in the northern and southern part of the flow. The second useful property of OPTICS is that not every point has to be part of a cluster. In fact, in the second and third rows of the figure, the grey points are identified as noise, i.e. they do not belong to any coherent set. This is different from many recent approaches that rely on graph partitioning algorithms for cluster detection. There, every point has to be part of a coherent set, which strongly limits the applicability to realistic geophysical flows. In our article, we apply OPTICS also to modelled trajectories in the Agulhas region, and find, as expected, Agulhas rings.
We show in our paper that a 20-year-old algorithm can be very successful in detecting finite-time coherent sets, even in a purely data-driven form, i.e. with very little additional heuristics or pre-processing of the data. It might well be that there exist even better algorithms that are suited for research questions in fluid dynamics. The Lagrangian fluid dynamics community should therefore explore more existing methods and algorithms from data sciences as these have the potential to greatly improve our understanding of fluid flows.