Tectonics and Structural Geology

The Makran accretionary wedge: an ideal natural laboratory to study accretionary processes.

Jonas Ruh June 16, 2020

Lower Miocene turbiditic (layered shale and sandstone) sequences of the Makran acretionary wedge. Credits: Jonas Ruh.

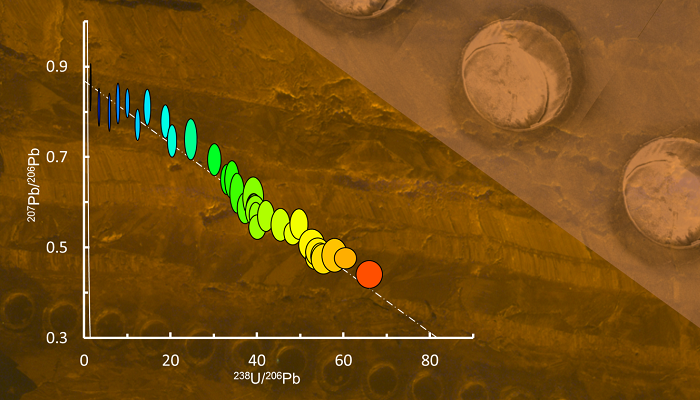
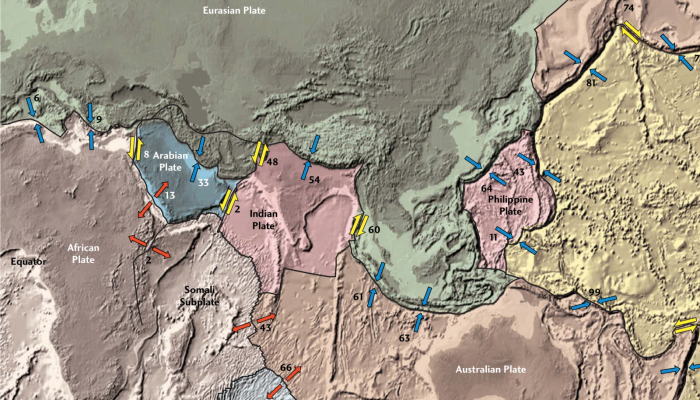
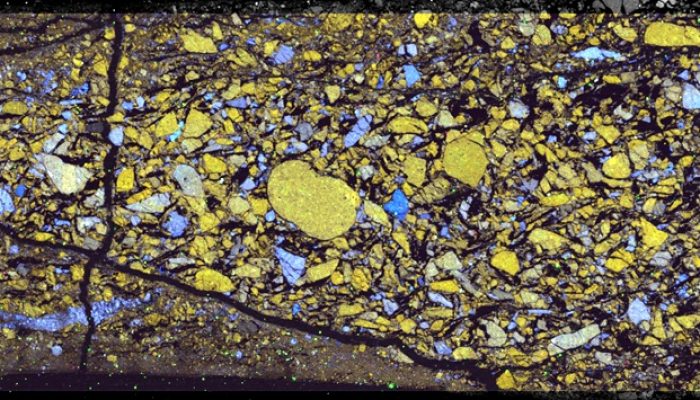
How does an accretionary wedge form? For this edition of Minds over Methods, we have invited Jonas Ruh, lecturer in the Structural Geology and Tectonics group of the Geological Institute at the Department of Earth Sciences, ETH Zürich, to tell us about the Makran accretionary wedge, one of the largest on Earth. He explains how the use of field observations and numerical modelling helped him to bet ...[Read More]

Analog models for teaching and more, even at home

Ágnes Király May 26, 2020

Ágnes Király is a postdoctoral research fellow at the Centre of Earth Evolution and Dynamics (CEED) at the University of Oslo, Norway. Ági has a background in geophysics, incorporating natural observations with numerical and analog models to study subduction zone processes. Ági has simulated subduction systems mostly in the Central Mediterranean. Working this spring will probably be somewhat diffe ...[Read More]

Neutrons and X-rays: 3D and 4D imaging in geoscience

Anne Pluymakers April 6, 2020

In-situ 4D Neutron imaging of imbibition of heavy water in an Indiana limestone (Cordonnier et al., 2019).

Anne Pluymakers is an assistant professor at TU Delft, whose hobbies include experimental rock mechanics and fluid-rock interaction. She focuses on the effects of fluids on mechanical behaviour of rocks at representative in-situ temperature and pressure conditions, with a strong focus on hydrochemical fluid-rock interaction. Investigating the microstructure of the rock and how it is altered is cri ...[Read More]

Minds over Methods: Dating deformation with U-Pb carbonate geochronology

EGU Guest blogger August 16, 2019

Cathodoluminescence image of calcite vein in background, with 100 micron laser ablation spots overlain top right and U-Pb isochron overlain left. Image credit: Nick Roberts

For this edition of Minds over Methods, we have invited Nick Roberts, a research scientist at the British Geological Survey, working within the Geochronology and Tracers Facility (GTF) running a LA-ICP-MS laboratory. Nick has a background in ‘hard-rock’ geology, incorporating geochemistry, geochronology, and magmatic and metamorphic petrology across a wide range of tectonic settings, and is now in ...[Read More]

Minds over Methods: Virtual Microscopy for Geosciences

Liene Spruženiece July 23, 2019

Information that can be extracted from a thin-section scan using the Virtual Microscope. All micrographs represent the same area within the thin section. From the upper left side: plain polarized light, crossed polarizers rotated by 0°, crossed polarizers rotated by 45°; from the lower left side: colour intensity map, colour saturation map, phase map. Credit: Liene Spruženiece

The next “Minds over Methods” blogpost is a group effort of Liene Spruženiece (left) – postdoctoral researcher at RWTH Aachen and her colleagues Joyce Schmatz, Simon Virgo and Janos L. Urai. The Virtual Microscope is a collaborative project between RWTH Aachen University and Fraunhofer Institute for Applied Information Technology (Schmatz et al., 2010; Virgo et al., 2016). In the ...[Read More]

Meeting Plate Tectonics – Nicolas Coltice

David Fernández-Blanco May 28, 2019

Credit: Grotzinger, J. and Jordan, T. (2014). Understanding Earth. [Plate boundaries by Peter Bird, UCLA]

These blogposts present interviews with outstanding scientists that bloomed and shape the theory that revolutionised Earth Sciences — Plate Tectonics. Get to know them, learn from their experience, discover the pieces of advice they share and find out where the newest challenges lie! Meeting Nicolas Coltice Nicolas Coltice graduated with a PhD from the École Normale Supérieure of Lyon, France. He ...[Read More]

Minds over Methods: Mineral reactions in the lab

EGU Guest blogger March 4, 2019

CL image of a sheared quartz-muscovite gouge. Credit: André Niemeijer.

Mineral reactions in the lab André Niemeijer, Assistant Professor, Department of Earth Sciences at Utrecht University, the Netherlands In this blogpost we will go on a tour of the High Pressure and Temperature (HPT) Laboratory at Utrecht University and learn about some of the interesting science done there. André’s main interest is fault friction and all the various processes that are invol ...[Read More]

Minds over Methods: Massively dilatant faults in Iceland – from surface to subsurface structures

Michael Kettermann & Christopher Weismüller January 29, 2019

View towards Ármannsfell (North) at Thingvellir. Lake Thingvallavatn on the right and the southern part of the Almannagjá massively dilatant fault on the left. Note the tilted blocks dipping towards the lake. Credit: Michael Kettermann.

In this Minds over Methods we don’t have one, but two scientists talking about their research! Michael Kettermann and Christopher Weismüller, both from Aachen University, explain us about the multidisciplinary approach they use to understand more about massively dilatant faults. How do they form and what do they look like at depth? Massively dilatant faults in Iceland – from surface to subsu ...[Read More]

Minds over Methods: What controls the shape of oceanic ridges?

Aurore Sibrant November 27, 2018

Bathymetry of an oceanic ridge. Credit: Ryan et al., 2009

In this edition of Minds over Methods, Aurore Sibrant, postdoc at Bretagne Occidentale University (France) explains how she studies the shape of oceanic ridges, and which parameters are thought to control this shape. By using laboratory experiments combined with observations from nature, she gives new insights into how spreading rates and lithosphere thickness influence the development of oceanic ...[Read More]

Minds over Methods: Experimental seismotectonics

Michael Rudolf March 26, 2018

Figure 1 - The analogue modelling laboratory at the GFZ-Potsdam (HelTec). Credit: Michael Rudolf

For our next Minds over Methods, we go back into the laboratory, this time for modelling seismotectonics! Michael Rudolf, PhD student at GFZ in Potsdam (Germany), tells us about the different types of analogue models they perform, and how these models contribute to a better understanding of earthquakes along plate boundaries. Experimental seismotectonics – Seismic cycles and tectonic ...[Read More]