Earth’s surface is covered by many kinds of granular materials, including sediments and soils. Below ground, grains are also widespread in unconsolidated deposits and fault zones; even polycrystalline rocks deep inside the Earth are made up of mineral grains. These materials deform under their own weight and external forces, but what forces act inside them? …[Read More]
To kick off the New Year, we have invited a guest author, Takafumi Maruishi, a researcher in the Research Division for Volcanic Disasters / Center for Volcano Research Promotion, National Research Institute for Earth Science and Disaster Resilience, Japan. He explains the scaling law of lava dome growth and its physical insight. Effusive eruptions—when magma …[Read More]
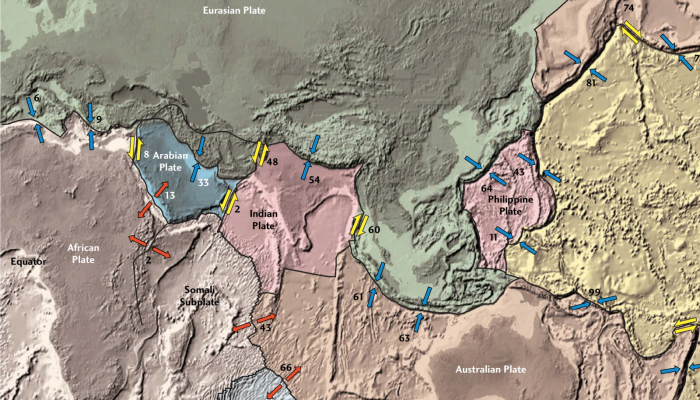
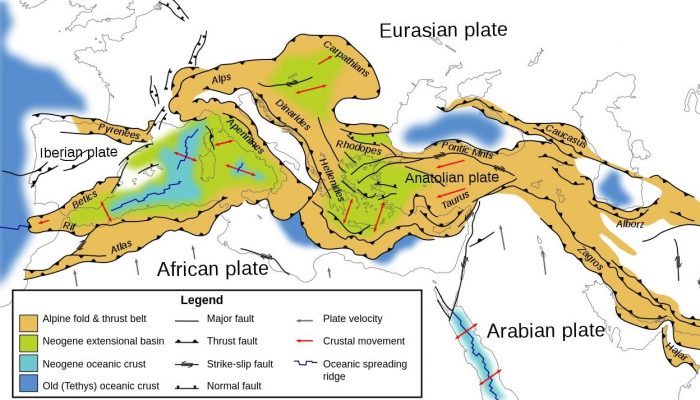
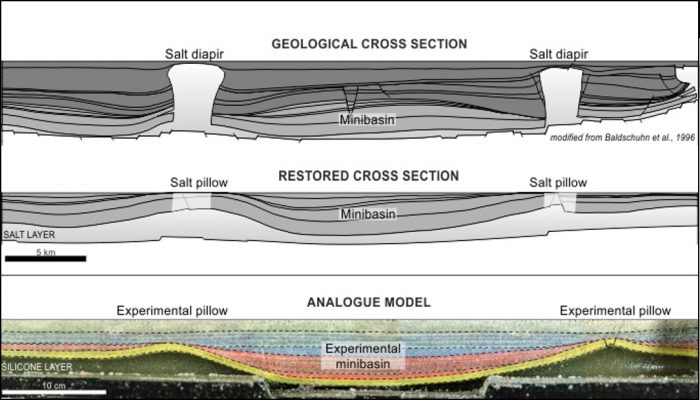
After a year and a half in which all of us have had to become accustomed to meeting our colleagues and collaborators only in digital space, it was finally time for an in-person conference again. From 19-23 of September 2021, the ninth edition of GeoMod took place in a conference center outside sunny Utrecht (the …[Read More]
Ágnes Király is a postdoctoral research fellow at the Centre of Earth Evolution and Dynamics (CEED) at the University of Oslo, Norway. Ági has a background in geophysics, incorporating natural observations with numerical and analog models to study subduction zone processes. Ági has simulated subduction systems mostly in the Central Mediterranean. Working this spring will …[Read More]
These blogposts present interviews with outstanding scientists that bloomed and shape the theory that revolutionised Earth Sciences — Plate Tectonics. Get to know them, learn from their experience, discover the pieces of advice they share and find out where the newest challenges lie! Meeting Barbara Romanowicz Barbara Romanowicz studied mathematics and applied physics and did two PhDs, one in astronomy …[Read More]
These blogposts present interviews with outstanding scientists that bloomed and shape the theory that revolutionised Earth Sciences — Plate Tectonics. Get to know them, learn from their experience, discover the pieces of advice they share and find out where the newest challenges lie! Meeting Jean-Philippe Avouac Prof. Jean-Philippe Avouac initially studied mathematics and physics during his undergraduate and graduate degrees. …[Read More]
These blogposts present interviews with outstanding scientists that bloomed and shape the theory that revolutionised Earth Sciences — Plate Tectonics. Get to know them, learn from their experience, discover the pieces of advice they share and find out where the newest challenges lie! Meeting Nicolas Coltice Nicolas Coltice graduated with a PhD from the École Normale Supérieure of Lyon, France. …[Read More]
In this edition of Minds over Methods, Aurore Sibrant, postdoc at Bretagne Occidentale University (France) explains how she studies the shape of oceanic ridges, and which parameters are thought to control this shape. By using laboratory experiments combined with observations from nature, she gives new insights into how spreading rates and lithosphere thickness influence the …[Read More]
For our next Minds over Methods, we go back into the laboratory, this time for modelling seismotectonics! Michael Rudolf, PhD student at GFZ in Potsdam (Germany), tells us about the different types of analogue models they perform, and how these models contribute to a better understanding of earthquakes along plate boundaries. Experimental seismotectonics – …[Read More]
How can we use GPS velocities to learn more about present-day plate motions and regional deformation? In this edition of Minds over Methods, one of our own blogmasters Mehmet Köküm shares his former work with you! For his master thesis at Indiana University, he used block modeling to better understand the plate motion and slip …[Read More]
