
The establishment of plate tectonics in the 1960s triggered a reappraisal of the development of mountain belts and facilitated the physics-based understanding of mountain building processes. Many models for mountain building were, however, mostly conceptual, and there was no appropriate theory that described the first-order mechanics of mountain belts. In 1983, this gap was – at least partially – filled, when three young scientists introduced the theory of critically tapered Coulomb wedge in their influential paper “Mechanics of Fold-and-Thrust Belts and Accretionary Wedges”. In essence, the Coulomb wedge theory simplifies tapered thrust belts and accretionary wedges as a material of Coulomb plastic rheology overlying a frictional basal fault. This approximation allowed the derivation of analytical solutions that describe the balance between rock strength, gravitational stresses arising from the surface slope, and basal shear stresses due to underthrusting. The theory exemplifies how changes in any of these parameters force the system toward a new balance.
The work of Davis and colleagues merged in exemplary manner geological observations, experimental data, and theoretical concepts into a unifying theory. Cross-section balancing and interpretation of seismic reflection profiles had revealed the characteristic wedge shape of fold-and-thrust belts and accretionary prisms, while analog models had illustrated the development of such thrust wedges in sandbox experiments. In addition, theoretical concepts had been established that considered the overall mechanics of thrust belts analogous to the mechanics of soil wedges that form in front of a moving bulldozer (e.g., Chapple, 1978). The major contribution by Davis and colleagues was to refine these existing ideas and to incorporate the Coulomb plastic rheology. This development eventually allowed to describe the mechanics of thrust wedges in terms of frictional strength μ and pore fluid pressure ratio λ.
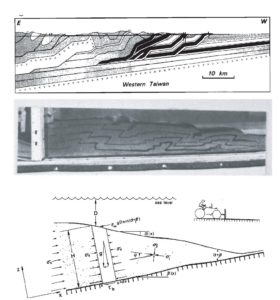
Up: Balanced cross section for western Taiwan, showing a wedge-shaped thrust belt overlying a basal fault. Centre: Analog model showing the development of a wedge-shaped thrust wedge. Down: Schematic diagram illustrating the force balance of a Coulomb wedge. From Davis et al. (1983).
In order to derive the analytical solutions, Davis and co-workers made a number of simplifications, some of which stimulated scientific debate. For example, the theory assumes a homogenous wedge, given by constant values of μ and λ. In the TS Must-Read discussion on Reddit, John Suppe notes in retrospect that this was unrealistic and that the pore fluid pressure conditions are never constant with depth (e.g., Suppe, 2014). Another much discussed aspect is the model limitations that arise from the Coulomb plastic rheology. The rheology restricts the model to the brittle frictional regime and the analytical solutions break down as soon as ductile deformation becomes relevant. Accordingly, the dynamics of Coulomb wedges cannot be easily transferred to entire orogens. Similarly, the basal fault of thrust wedges may be located within evaporites like salt or anhydrite, as pointed out by Akinbobola Akintomide on Reddit. In this case, basal shear stresses are not appropriately described by the Coulomb failure criterion.
Many of the assumptions and simplifications that went into the “Mechanics of Fold-and-Thrust Belts and Accretionary Wedges” have motivated a large number of follow-up studies, just like the implications of this work did. In particular, the Coulomb wedge theory laid the foundation for the study of climate-tectonic interactions and influenced the development of numerical approaches that account for both brittle and ductile deformation (e.g., Beaumont et al., 1992). More recently, the Coulomb wedge theory was expanded by elasticity, which allowed us to consider temporal variations in strength, stress, and deformation in great earthquake cycles (Wang & Hu, 2006). The Coulomb wedge theory has thereby maintained its topicality after almost forty years.
John Suppe, Armin Dielforder, Akinbobola Akintomid, and Gianluca Frasca contributed to the discussion on reddit.
Written by Armin Dielforder, Akinbobola Akintomide, Patricia Cadenas Martínez, and the TS Must-Read team
References
Beaumont C., Fullsack P., Hamilton J., 1992. Erosional control of active compressional orogens. In: McClay K.R. (eds) Thrust Tectonics. Springer, Dordrecht. https://doi.org/10.1007/978-94-011-3066-0_1
Chapple, W. M., Mechanics of thin-skinned fold-and-thrust belts. Geol. Soc. Am. Bull., 89, 1189-1198, 1978. https://doi.org/10.1130/0016-7606(1978)89<1189:MOTFB>2.0.CO;2
Davis, D., Suppe, J., Dahlen, F.A., 1983. Mechanics of fold-and-thrust belts and accretionary wedges. J. Geophys. Res., 88, 1153-1172. https://doi.org/10.1029/JB088iB02p01153
Suppe, J., 2014. Fluid overpressures and strength of the sedimentary upper crust. J. Struct. Geol. 69, 481-492. https://doi.org/10.1016/j.jsg.2014.07.009.
Wang, K., Hu, Y., 2006. Accretionary prisms in subduction earthquake cycles: The theory of dynamic Coulomb wedge. J. Geophys. Res. 111, B06410. https://doi.org/10.1029/2005JB004094.


