Summer vacations are finally here! Like every year, many of us are ready to travel and explore new and exciting destinations. And of course, the GPS on our phones will be an indispensable travel companion! Did you know that GPS (or GNSS) positioning is one of the traditional geodetic techniques? Come along to discover how this technique can find your location in the world and the various applications of GNSS positioning!
First, what is GNSS?
While we often say “GPS” to refer to any location service, the actual meaning and origin of the term are less commonly known. The Global Positioning System (complete name of GPS) is a US-owned navigation system that nowadays includes a set of 32 satellites that transmit the necessary information so that any receivers (for example, our phones) can compute their position [1]. But GPS isn’t the only navigation system out there. In recent years, Europe has launched its own system, Galileo [2], and countries such as Russia (GLONASS) and China (BeiDou system) also have their own systems in orbit. The term GNSS, Global Navigation Satellite System, refers to the ensemble of all of them. Many modern positioning devices (including some smartphones [3]) track all kinds of GNSS satellites to get more complete information and a higher positioning accuracy.
Finding our position through trilateration
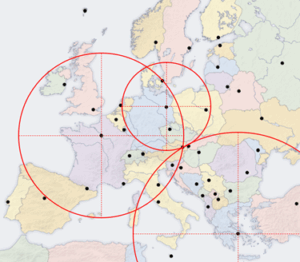
Finding the answer to the game through trilateration. Courtesy of Leire Retegui-Schiettekatte, modified from an original image by User: Highpriority, CC BY-SA 3.0, via Wikimedia Commons)
As we were talking about travelling, let’s play a little game. There’s a European capital located 524 km from Berlin, 1,033 km from Paris, and 1,283 km from Athens. Can you guess which one it is? Many of you might have visited this city in the past year. If you are still in doubt, the answer can be easily found: we just need to take a map and a compass and draw a circle around each city with the distances above as radii. The place where the three circles intersect will point to the city we seek.
This method, called trilateration, is what GNSS receivers use to compute their position. In this case, the reference points are the GNSS satellites orbiting around the Earth, and the receiver then uses the electromagnetic radio signal transmitted from the satellites to compute the distance to each of them. Actually, the receiver first computes the time that the signal took to travel from the satellite to the receiver (ΔT), and then multiplies it by the speed of light in vacuum (c, around 3∙108 meters per second) to obtain the distance estimate (ΔD = c∙ΔT) [4]. Once these distances (ΔD) are calculated, the positions of the satellites must also be known to perform trilateration. Each satellite is aware of its own position with respect to a global reference frame (for an exciting read about reference frames, see our post here!), and sends this information to the receiver by encoding it in the GNSS signal itself.
In order to be able to fully constrain its location (and its clock bias), the receiver must be able to receive information from at least four satellites. Buildings and vegetation can act as a barrier for GNSS signals. That’s why, if our phone’s GPS isn’t working well in a city, we should try to move to a wider square where a bigger part of the sky is visible. The device is then ready to perform trilateration and find its location!
Perfecting the positioning through error corrections
But is this time-based distance (ΔD = c∙ΔT) really accurate? Coming back to our little game, imagine that instead of providing you the distance of the “mystery city” with respect to Berlin, Paris, and Athens, I give you the information in terms of train travel time. The computation will then become much more uncertain: the train travel times can be affected by delays in the departure, arrival, state of the rails, weather, … and countless other factors.
This is also the case with GNSS measurements. When computing the travelling time ΔT, that time includes (and is not limited to), for example, the delay the signal might have when leaving the satellite, the delay it might get when arriving at the receiver, as well as delays induced by interaction of the electromagnetic wave with the atmosphere of the Earth [4]. That is why the time-based distance ΔD is usually referred to as the “apparent distance”, “pseudodistance”, or “pseudorange”. Some corrections need to be applied to this first estimate to get the “real” distance.
Several techniques can be used to correct each of these errors, which include using the information provided by the GNSS signals, physical or weather prediction models, and even additional observations. Depending on the corrections applied, we might achieve a positioning accuracy ranging from a few meters down to a millimeter or even less.
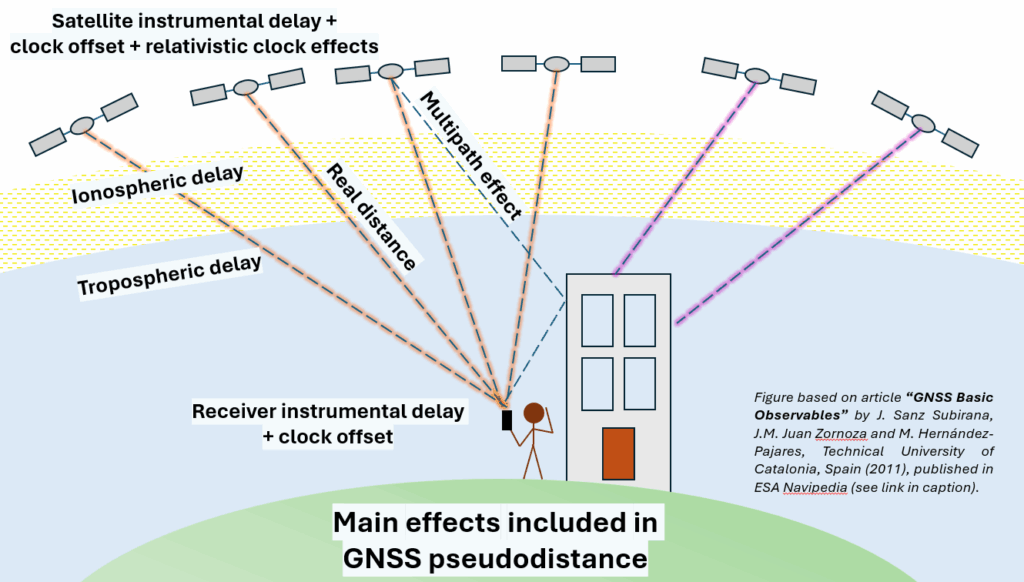
Main effects included in GNSS pseudodistance. Courtesy of Leire Retegui-Schiettekatte, based on article “GNSS Basic Observables” by J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain (2011), published in ESA Navipedia.
The various applications of GNSS positioning
GNSS-based positioning can be used for a wide range of applications, with each application demanding different accuracy levels [5]. The civil applications are probably the most well-known: GPS/GNSS services in smartphones and cars typically offer meter-level accuracy, making our everyday life easier and helping us reach our destinations. GNSS devices are also used in public transport (for example, trains, boats, and planes) to help track the location of these vehicles, for which a more accurate and reliable positioning is required.
Other applications, like land surveying, require higher positioning accuracy. Professional GNSS receivers are used to find the position of landmarks or points in a terrain, with variable accuracy above or below a centimeter, depending on the technique used and the corrections applied. Military applications—one of the original drivers behind GNSS development—also require a high positioning accuracy.
GNSS positioning at the millimeter-level accuracy is also used in Earth sciences. GNSS receivers installed on stable bedrock can be used to measure the deformation of the land caused by geodynamics (for example, tectonics or earthquakes). On our blog, you can dive into exciting scientific GNSS measurement campaigns in East Africa or even in Antarctica!
These are only some of the uses of GNSS technologies, but new, original, and innovative applications still continue to emerge in science and industry. Who knows which additional applications the future will bring!
References
– Edited by Marius Schlaak