After our first edition of Minds over Methods, which was about Numerical Modelling, we now move to Rock Experiments! How can rock experiments be used to study processes within the Earth? We invited Giacomo Pozzi, PhD student at Durham University, to explain us how he uses rock experiments to study fault behaviour during earthquakes.
Experimental earthquakes to understand the weak behaviour of faults.
Giacomo Pozzi, PhD student at Durham University
As seismic slip along faults accommodates large deformations in the upper crust, the intriguing absence of significant heat flow anomalies (which are expected to be produced by intense energy dissipation during slip) along major geological bodies like the S. Andreas fault pushed the researchers to start conceiving a new, dynamic theory of friction, which eventually led to the concept of low frictional strength of faults during propagation of earthquakes.
Fig 1. the Rotary apparatus
In the past two decades, the development of machines capable of shearing natural materials made it possible to achieve direct, experimental evidences of how friction in rocks (and gouges, when pulverised) drops from Byerlee’s values (μ=0.6-0.8) towards zero when approaching seismic velocities (>10 cm/s) and this independently of the rock composition.
However, even though a common bulk behaviour is witnessed, the weakening mechanisms that operate at the microscale are strongly dependent on the mineralogy and, despite a large amount of literature focused on this research, they are still poorly understood as their physic is an evergreen matter of debate.
My Ph.D. focuses on a weakening mechanism that has been recently proposed to occur in carbonate faults: viscous flow by grain boundary sliding, a diffusion creep dominated process particularly efficient in fine grained aggregates. In order to verify and characterise this hypothesis we try to reproduce coseismic shear conditions in pure calcite (CaCO3) gouges with a Low to High Velocity Rotary (LHVR) apparatus (Figure 1). This machine allows to simulate arbitrary amounts of slip in a thin volume of gouge, our experimental fault core, which is squeezed between two hollow cylinders. A piston located in the lower part of the apparatus lifts the lower cylinder producing an axial load (up to 25MPa) perpendicular to the plane of slip while the top cylinder spins at angular velocities up to 1500rpm (1.4 m/s tangential velocity at the reference radius).
During the experiments we record different mechanical parameters that can be processed to obtain: displacement, velocity, axial stress, shear stress, axial displacement and, with an opportune equation, the estimated temperature in the shear zone. The ratio between shear stress and axial stress gives the friction coefficient that produces a classic weakening profile when plotted against the displacement as in the graph of figure 2, where are evident two main stages: pre-weakening (μ>0.6) and weakening stage (μ<0.3).
At the end of each experiment we carefully remove the sheared sample in order to make microstructural analysis. We describe the architecture of the shear zone mainly by acquiring electron backscattered (EBS) images (figure 3) on polished sections of the samples using a scanning electron microscope. We are also planning to use cathodoluminescence and EBS diffraction to study in detail the distribution of strain, temperature and hidden geometries.
By coupling the mechanical data and the microstructural analysis of experiments stopped at different amounts of slip we are able to reconstruct the evolution of the shear zone, including the transition between a pre-weakening brittle behaviour to the steady state weakening stage where ductile-plastic processes are dominant. Understanding how the internal architecture of the shear zone changes with time and measuring its geometrical features is of paramount importance to achieve a quantitative description of the processes, which can lead to new physical laws.
With our experiments we are trying to link a qualitative description of complex natural processes and quantitative simulations based on the current physical knowledge. As a matter of fact, the obtained microstructures can be compared to natural equivalents while mechanical data and inferred laws can be implemented in numerical models.
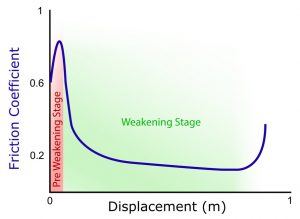
Fig 2. Weakening profile
Fig 3. SEM BSE image of a cross section of the slip zone
