
With their milestone article in Journal of Structural Geology (Fossen and Tikoff, 1993) and its companion article in Tectonophysics (Tikoff and Fossen, 1993), the authors marked a step forward for the quantification of strain in the deep crust. These articles popularized a new approach, the deformation matrix.
An easy solution to quantify strain in finite geological systems is to find continuous pre-deformation structures or levels. Whereas this is doable for (most) structures at the surface where sediments are often offering a myriad of such markers, identifying any marker at depth is commonly challenging. This called for alternative approaches, notably by quantifying the finite strain in the zone of deformation itself. Yet, this step remained a hard one for a long time, as deformation is rarely solely pure shear or simple shear, but a combination of pure shear, simple shear, and volume change (variation in porosity, metamorphic reactions…). Although some solutions were already proposed at that time (e.g., Ramsay, 1980; see related blog post), models circumvented the combination of strain by applying alternatively pure shear and simple shear deformation increments (Fig. 1). This implies, in turn, that any finite strain ellipsoid may source from an infinite composition of pure shear and simple shear increments. Another point of discussion is related to the fact that the event sequence is also important: applying a pure shear followed by a simple shear does not lead to the same finite strain as applying simple shear followed by pure shear (Fig. 1a,b).
The solution proposed by Fossen and Tikoff offered a new mathematical tool to the Earth Sciences community, the deformation matrix, to derive the simplest and unique combination of pure shear, simple shear and volume change for any deformed material undergoing steady flow. This is, for any material in which the principal axes of instantaneous stretching and the kinematic vorticity Wk are constant (Fig. 1c). Their work was notably built on earlier works implementing deformation matrices such as Ramberg (1975), Sanderson (1976) and others, but was generalized and simplified to make it easier to apply to geological problems, in both 2D and 3D.
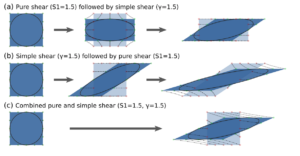
Figure 1: 2D synthetic squares deformed by (a) pure shear followed by simple shear deformation, (b) simple shear followed by pure shear deformation, and (c) combined pure shear and simple shear deformation. Note the difference between the resulting shapes.
Proposing a new mathematical approach, the authors had to derive several equations, making the article rather hard to handle by geologists. Yet, their manuscript is very well written by keeping the demonstrations as simple as possible and explaining in an intuitive way the influence of the various parameters.
Their approach also permits to elegantly model the change in orientation of elements during any deformation pattern. Some consequences are therefore detailed at the end of the article, by its application to transpression and transtension. They demonstrate that the long-axis of the deformation ellipsoid (i.e., the lineation) is always horizontal for transtension, switches from horizontal to vertical for gentle transpression, and is always vertical for highly transpressive deformation. Vice-versa, they framed the method to estimate the pure vs. simple shear ratio of natural strain zones by analysing the finite orientation of (elongated) elements in deformed rocks (i.e., the vorticity analysis; Passchier 1987; Xypolias, 2010).
Benoît Petri, Arnab Roy, David Fernández-Blanco and the TS Must Read team
References
Fossen, H., Tikoff, B., 1993. The deformation matrix for simultaneous simple shearing, pure shearing and volume change, and its application to transpression-transtension tectonics. J. Struct. Geol. 15, 413–422. https://doi.org/10.1016/0191-8141(93)90137-Y
Passchier, C.W., 1987. Stable positions of rigid objects in non-coaxial flow – a study in vorticity analysis. J. Struct. Geol. 9, 679–690. https://doi.org/10.1016/0191-8141(87)90152-0
Ramberg, H., 1975. Particle paths, displacement and progressive strain applicable to rocks. Tectonophysics 28, 1–37. https://doi.org/10.1016/0040-1951(75)90058-X
Ramsay, J.G., 1980. Shear zone geometry: A review. J. Struct. Geol. 2, 83–99. https://doi.org/10.1016/0191-8141(80)90038-3
Sanderson, D.J., 1976. The superposition of compaction and plane strain. Tectonophysics 30, 35–54. https://doi.org/10.1016/0040-1951(76)90136-0
Tikoff, B., Fossen, H., 1993. Simultaneous pure and simple shear: the unifying deformation matrix. Tectonophysics 217, 267–283. https://doi.org/10.1016/0040-1951(93)90010-H
Xypolias, P., 2010. Vorticity analysis in shear zones: A review of methods and applications. J. Struct. Geol. 32, 2072–2092. https://doi.org/10.1016/j.jsg.2010.08.009

