
The Must-Read paper by Cowie and Scholz (1992) uses theory from fracture mechanics to explain fault growth and fault displacement profiles. The article initially points out the weaknesses in previous work, specifically highlighting how the abrupt termination of displacement profiles at fault tips would imply an infinite stress in the surrounding material. The paper then introduces a physical model in which the displacement profile gradually tapers out towards the tips of the fault, with a zone around the fault tips deforming inelastically. The authors compare the model to fault data from different tectonic regions and different rock types. Specifically, they look at the displacement profiles observed within faults, and the relationship between maximum displacement and fault length. The last part of the paper explores what their findings imply in terms of rock shear strength – the value of the forces needed for rocks to start sliding – and fracture energy involved in both earthquakes and lab experiments.
A key element of this paper is the introduction of their fault model based on fracture mechanics, providing a solid theoretical basis to explore faults from laboratory (cm) to crustal (km) scales. They use a cohesive zone fracture model called a ‘Dugdale model’ (Fig. 1), whose predictions for displacement profiles compare very well with natural observations, making a convincing case for its validity. Another important outcome of this study is the estimate on the upper bounds of crustal shear strength, bearing relevance to our mechanical understanding on the large-scale evolution of fault systems. The main take home of the study is that the work required to propagate a fault is proportional to the fault length; this provides an explanation on why the fracture energy calculated for earthquake ruptures is many orders of magnitude greater than for its laboratory fracture equivalents.
Perhaps one of the most influential consequences of this paper – in combination with its sibling-paper titled “Displacement-length scaling relationship for faults: data synthesis and discussion” (also Cowie and Scholz 1992) – is that these authors provided a convenient overview on fault displacement-length relationships. In nature, it is often challenging to obtain estimates of fault displacements, but scaling laws allow for quick and easy first-order estimates by using the typically easier-to-assess fault length. After this Must-Read paper came out, many similar scaling attempts followed. Good overviews are provided in Kim and Sanderson (2005), and in Rotevatn et al. (2019); the latter is another Must-Read paper that will be discussed later in this series.
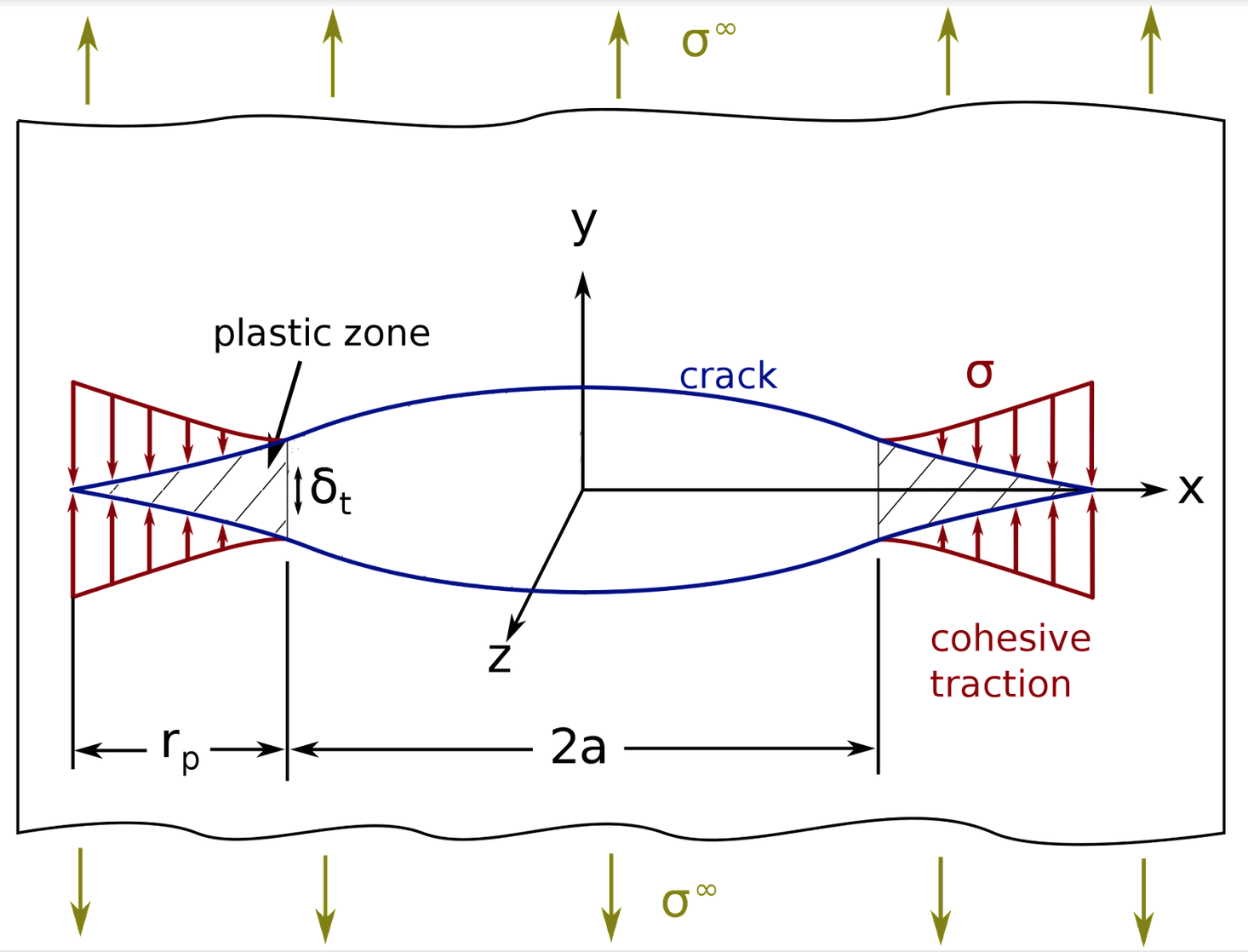
Figure 1: Diagram depicting cohesive zone fracture models, a family of models following the original Dugdale fracture model (1960). 2a represents the crack length, ẟt the crack separation displacement, σ the cohesive traction, σ∞ the remote applied stress and rp the length of the plastic (inelastic) zone (Source). In the fault model of Cowie and Scholz (1992), faults propagate when the cohesive traction exceeds the rock strength of the surrounding material.
In the discussion on Reddit, Gino de Gelder points out how the findings on bell-shaped displacement profiles here are relevant and observable on the scale of outcrops, but also on the scale of rifts. Akinbobola Akintomide highlights how it’s elegant that the fault growth model not only describes lateral differences in a fault, but temporal differences at the same time. He furthermore gives a field example from an earthquake in South Iceland in 1912 that evidences non-elastic fault propagation (further reading: Bjarnason et al., 1993). Finally, David Fernández-Blanco describes how fantastic it is that the paper provides scaling predictions between fault displacement and fault length across scales, and suggests that all the combined Cowie and Scholz (1992) papers could easily lay the groundwork for any PhD in fault mechanics.
Adriana Guatame-Garcia, Akinbobola Akintomide, Gino de Gelder and the TS Must Read team
References
Bjarnason, I. T., Cowie, P., Anders, M. H., Seeber, L., & Scholz, C. H. (1993). The 1912 Iceland earthquake rupture: Growth and development of a nascent transform system. Bulletin of the Seismological Society of America, 83(2), 416-435. DOI: 10.1785/BSSA0830020416
Cowie, P. A., & Scholz, C. H. (1992). Physical explanation for the displacement-length relationship of faults using a post-yield fracture mechanics model. Journal of Structural Geology, 14(10), 1133-1148. DOI: 10.1016/0191-8141(92)90065-5
Cowie, P. A., & Scholz, C. H. (1992). Displacement-length scaling relationship for faults: data synthesis and discussion. Journal of Structural Geology, 14(10), 1149–1156. DOI: 10.1016/0191-8141(92)90066-6
Dugdale, D. S. (1960). Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8(2), 100-104. DOI: 10.1016/0022-5096(60)90013-2
Kim, Y. S., & Sanderson, D. J. (2005). The relationship between displacement and length of faults: a review. Earth-Science Reviews, 68(3-4), 317-334. DOI: 10.1016/j.earscirev.2004.06.003
Rotevatn, A., Jackson, C. A. L., Tvedt, A. B., Bell, R. E., & Blækkan, I. (2019). How do normal faults grow?. Journal of Structural Geology, 125, 174-184. DOI: 10.1016/j.jsg.2018.08.005



